Please include all the steps and answers, thank you!!
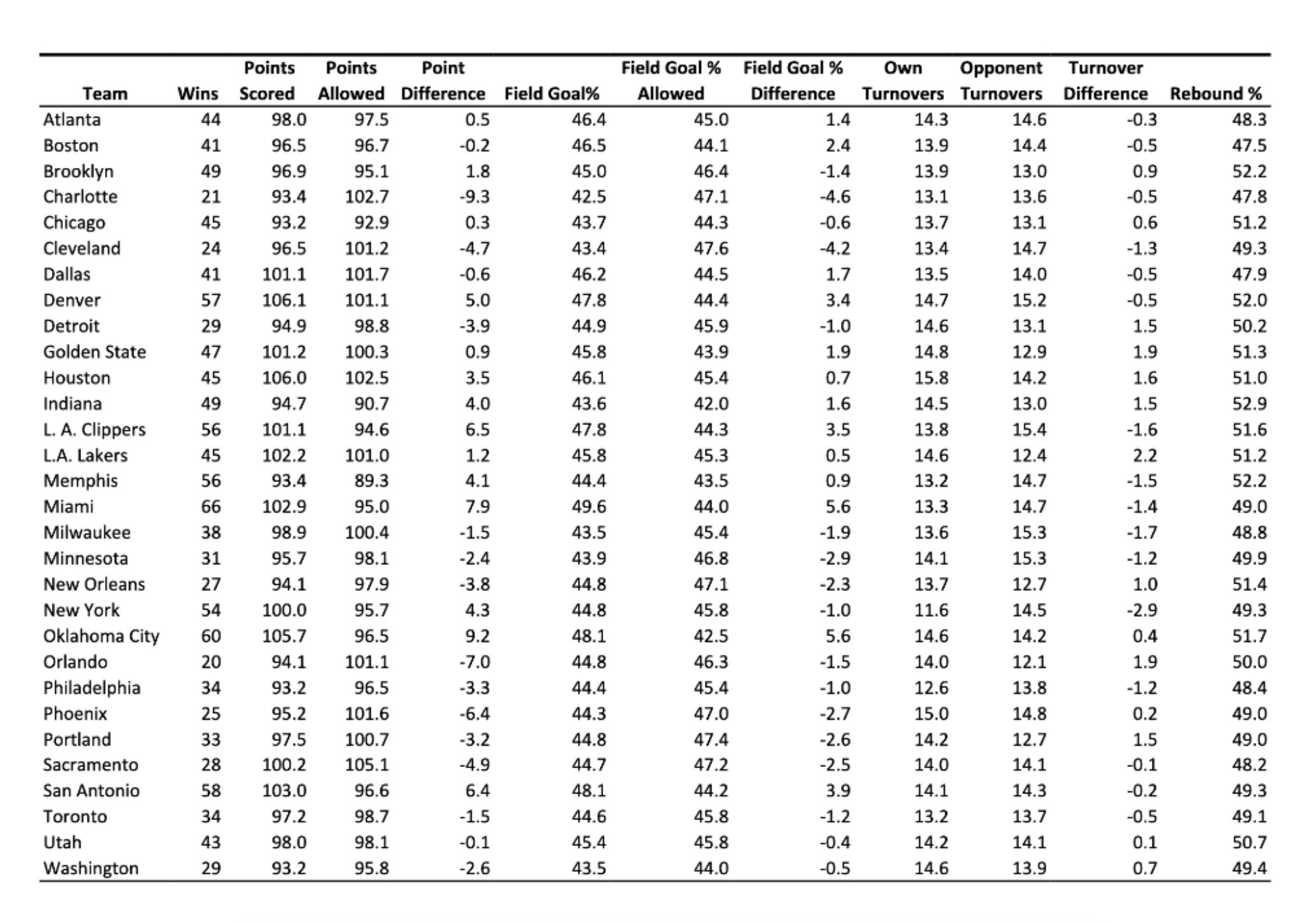
Professional basketball has become a sport that generates interest around the world. The Excel file NBA summarizes results of the US National Basketball Association, in a particular year. You want to develop a regression model to predict the number of wins achieved by each NBA team, based on the average point difference and the average field goal percentage difference between the team and its opponent. Using the Data Analysis add-in, follow the steps listed below and answer the following questions. 6.1 Perform multiple linear regression analysis. State the regression equation. 6.2 Interpret the meaning of the slope coefficients obtained. Explain whether the intercept coefficient has a practical interpretation or not in the context of this study. 6.3 Based on your model, predict wins for a team with average point difference of 6, and average field goal % difference of 3.5. 6.4 Based on the residual plots received in your model, comment on the plausible satisfaction of the normal residual (noise) model assumptions. 6.5 Do you have to use the Durbin-Watson statistic? 6.6 Repeat steps 6.1 to 6.4 to develop a multiple linear regression model that also considers possible interaction between average point difference, and average field goal % difference. Draw your conclusion. 6.7 Based on the results received so far, select and develop a simple linear regression model, repeating steps 6.1 to 6.4 for this model. Draw your final conclusion. Submit both your answers summarized in a Word doc file, and your complete Excel solution file. In the Excel file, use the Data Analysis add-in, and store the results in separate (appropriately named) tabs. Points Points Point Field Goal % Field Goal % Own Opponent Turnover Team Wins Scored Allowed Difference Field Goal% Allowed Difference Turnovers Turnovers Difference Rebound % Atlanta 44 98.0 97.5 0.5 46.4 45.0 1.4 14.3 14.6 -0.3 48.3 Boston 41 96.5 96.7 -0.2 46.5 44.1 2.4 13.9 14.4 -0.5 47.5 Brooklyn 49 96.9 95.1 1.8 45.0 46.4 -1.4 13.9 13.0 0.9 52.2 Charlotte 21 93.4 102.7 -9.3 42.5 47.1 -4.6 13.1 13.6 -0.5 47.8 Chicago 45 93.2 92.9 0.3 43.7 44.3 -0.6 13.7 13.1 0.6 51.2 Cleveland 24 96.5 101.2 -4.7 43.4 47.6 -4.2 13.4 14.7 -1.3 49.3 Dallas 41 101.1 101.7 -0.6 46.2 44.5 1.7 13.5 14.0 -0.5 47.9 Denver 57 106.1 101.1 5.0 47.8 44.4 3.4 14.7 15.2 -0.5 52.0 Detroit 29 94.9 98.8 3.9 44.9 45.9 -1.0 14.6 13.1 1.5 50.2 Golden State 47 101.2 100.3 0.9 45.8 43.9 1.9 14.8 12.9 1.9 51.3 Houston 45 106.0 102.5 3.5 46.1 45.4 0.7 15.8 14.2 1.6 51.0 Indiana 49 94.7 90.7 4.0 43.6 42.0 1.6 14.5 13.0 1.5 52.9 L. A. Clippers 56 101.1 94.6 6.5 47.8 44.3 3.5 13.8 15.4 -1.6 51.6 L.A. Lakers 45 102.2 101.0 1.2 45.8 45.3 0.5 14.6 12.4 2.2 51.2 Memphis 56 93.4 89.3 4.1 44.4 43.5 0.9 13.2 14.7 -1.5 52.2 Miami 66 102.9 95.0 7.9 49.6 44.0 5.6 13.3 14.7 -1.4 49.0 Milwaukee 38 98.9 100.4 -1.5 43.5 45.4 -1.9 13.6 15.3 -1.7 48.8 Minnesota 31 95.7 98.1 -2.4 43.9 46.8 -2.9 14.1 15.3 -1.2 49.9 New Orleans 27 94.1 97.9 3.8 44.8 47.1 -2.3 13.7 12.7 1.0 51.4 New York 54 100.0 95.7 4.3 44.8 45.8 -1.0 11.6 14.5 -2.9 49.3 Oklahoma City 60 105.7 96.5 9.2 48.1 42.5 5.6 14.6 14.2 0.4 51.7 Orlando 20 94.1 101.1 -7.0 44.8 46.3 -1.5 14.0 12.1 1.9 50.0 Philadelphia 34 93.2 96.5 -3.3 44.4 45.4 -1.0 12.6 13.8 -1.2 48.4 Phoenix 25 95.2 101.6 -6.4 44.3 47.0 -2.7 15.0 14.8 0.2 49.0 Portland 33 97.5 100.7 -3.2 44.8 47.4 -2.6 14.2 12.7 1.5 49.0 Sacramento 28 100.2 105.1 -4.9 44.7 47.2 -2.5 14.0 14.1 -0.1 48.2 San Antonio 58 103.0 96.6 6.4 48.1 44.2 3.9 14.1 14.3 -0.2 49.3 Toronto 34 97.2 98.7 -1.5 44.6 45.8 -1.2 13.2 13.7 -0.5 49.1 Utah 43 98.0 98.1 -0.1 45.4 45.8 -0.4 14.2 14.1 0.1 50.7 Washington 29 93.2 95.8 -2.6 43.5 44.0 -0.5 14.6 13.9 0.7 49.4