(Please read the instructions carefully to solve the program) (The Java Class should be called LinkedPolynomial.java) (IT SHOULD BE WRITTEN IN JAVA)  Polynomial Implementation (ADT Implementation Using Linked Structures) 

Summary

Implement the Polynomial interface using a private linked Node class. (NOT a LinkedList or any other data structure.) Your implementation must provide suitable code for each of the operations in that interface. It must also have a zero-arguments constructor. (The default constructor may be suitable.)

Details

I have provided you with an interface for a Polynomial data type. It contains only some basic methods (no methods for mathematical operations on full Polynomials, for example). I have also provided you with a sample client program.

You SHOULD NOT modify those files.

I assume you are familiar with polynomials, but I have provided some information in the Polynomial javadoc.

You must use a private Node class in your implementation. You are not allowed to make use of any reference types that you have not defined yourself.

I recommend that you keep the Nodes in the order they get printed in. Thus the Polynomial 0.2x⁵ + x² + -3.5x + 2.0 would be kept as the linked structure:

head [*] --> [0.2|5|*] --> [1.0|2|*] --> [-3.5|1|*] --> [2.0|0|/]

where the *s represent references and the / represents a null reference.

That's a recommendation, which means you don't have to do it that way!.

You might not need to add a constructor to your class, but if you do make sure you have a no-arguments constructor.

The method getDegree should be very easy.

The methods evaluateAt and getCoefficient should be pretty easy.

The add and toString methods will be somewhat harder. I recommend you start with a partial implementation of add that just places the given term at the front of the list of terms. Then move on to toString and get that printing each term the way you want it printed.

The output will not be entirely the way it needs to be, but each term printed should be OK. For example: you might see

-x^2 + 3.0x^5 + -5.1x^3 + 0.2x^5 + x^2 + 3.5x + 2.0

After you've got toString working as you want, you can then move on to making add behave properly.

BONUS POINTS for replacing + signs with - signs and integer coefficients without decimal points. For example, printing

0.2x⁵ + x² + -3.5x + 2.0

as

0.2x^5 + x^2 - 3.5x + 2

Be careful that you don't mess up the first term, which has no + sign in front of it to be changed. Thus we should not see

-0.2x⁵ + -3.5x

as

0.2x^5 - 3.5x

______________________________________________________________________ 

Polynomial.java

/** * An interface with some basic polynomial methods. A polynomial is the sum of * several terms, each of which is a multiple of a power of x. The powers are * non-negative integers. The multiple is double, and terms multiplied by zero * are ignored. The multiplier for a term is called its coefficient. * For example: * 
 * 0.2x5 + 1x2 + -3.5x1 + 2x0 * 
 has four (non-zero) terms, as follows: * 

* * * * * *

coefficient	power
0.2	5
1.0	2
-3.5	1
2.0	0

*

* Terms are printed in order from highest power to lowest power. Each (non- * zero) term shows the coefficient and the power of x, except for terms with a * coefficient of one, or a power of one or less. The coefficient one may be * left out. Terms with power one leave the power off, and terms with power zero * leave both the power and the x off. Other powers are preceded with a "hat" * symbol (^, also known as a circumflex). For example, the polynomial above * could be written as: * 0.2x^5 + x^2 + -3.5x + 2.0 * * Polynomials with no terms are written as zero. *

* The highest power in the polynomial is called the degree of the * polynomial. If there are no terms in the polynomial, then the power is zero. *

* Polynomials are evaluated by replacing the x with a given value and * calculating the sum. For example, the polynomial above at 2.0 would evaluate * to *

 * 0.2×25 + 1×22 + -3.5×21 + 2×20 * = 0.2×32 + 1×4 + -3.5×2 + 2×1 * = 6.4 + 4 + -7 + 2 = 5.4 * 

* * @author Mark Young (A00000000) */ public interface Polynomial { /** * The power of the term with the highest power. * * @return */ public int getDegree(); /** * The coefficient of the x^power term. * * @param power the power we want the coefficient of * @return the coefficient of the term with that power, or zero if no such * term exists */ public double getCoefficient(int power); /** * Evaluate the polynomial at the given point. * * @param x the point to evaluate the polynomial at * @return the value of the polynomial at that point */ public double evaluateAt(double x); /** * Create a String representation of this polynomial. Only terms with non- * zero coefficients form part of the String representation. * * @return a String representing this polynomial */ public String toString(); /** * Add another term to this polynomial. If this polynomial already has a * term with the same power, the terms are combined, which might result in * that term being "zeroed out" and removed from the polynomial. * * This method returns the polynomial is was called on, allowing the method * to be called repeatedly on one object to add multiple terms. For example, * poly.add(3, 2).add(2, 1).add(7, 0) adds * 3x² + 2x + 7 to poly. * * @param coefficient the coefficient of the term to add * @param power the power of the term to add * @return the same polynomial, as modified by the addition of the term */ public Polynomial add(double coefficient, int power); }

______________________________________________________________________

TestPolynomials.java:

import java.util.Scanner; /** * A linked implementation of the Polynomial interface. * * @author Mark Young (A00000000) */ public class TestPolynomials { /** * @param args the command line arguments */ public static void main(String[] args) { // TODO code application logic here // test(new LinkyStubby()); test(new LinkedPolynomial()); } /** * Run some tests on the given Polynomial. * * @param poly the Polynomial to test */ private static void test(Polynomial poly) { // show the original polynomial show(poly); // add a constant term poly.add(2.0, 0); show(poly); // add a linear term poly.add(3.5, 1); show(poly); // add a quadratic term poly.add(1.0, 2); show(poly); // jump up a couple of powers poly.add(0.2, 5); show(poly); // go back and add a lower power poly.add(-5.1, 3); show(poly); // adjust the coefficient of a power poly.add(3, 5); show(poly); // zero out a term poly.add(-1.0, 2); show(poly); // zero out all remaining terms poly.add(-3.2, 5).add(5.1, 3).add(-3.5, 1).add(-2, 0); show(poly); try { // try to add a term with a negative power poly.add(5.0, 1).add(10.0, -1); System.out.println("Added a negative power term!"); } catch (IllegalArgumentException iae) { System.out.println("Did not add a negative power term,"); System.out.println("because " + iae); } show(poly); } /** * Show that all the Polynomial methods work for this Polynomial. * * @param poly the Polynomial to show */ private static void show(Polynomial poly) { System.out.println("poly(x) == " + poly); System.out.println("poly.getDegree() == " + poly.getDegree()); for (int i = 0; i  
______________________________________________________________________
 
*OUTPUT SHOULD LOOK LIKE THE ATTACHED PICTURES*
 
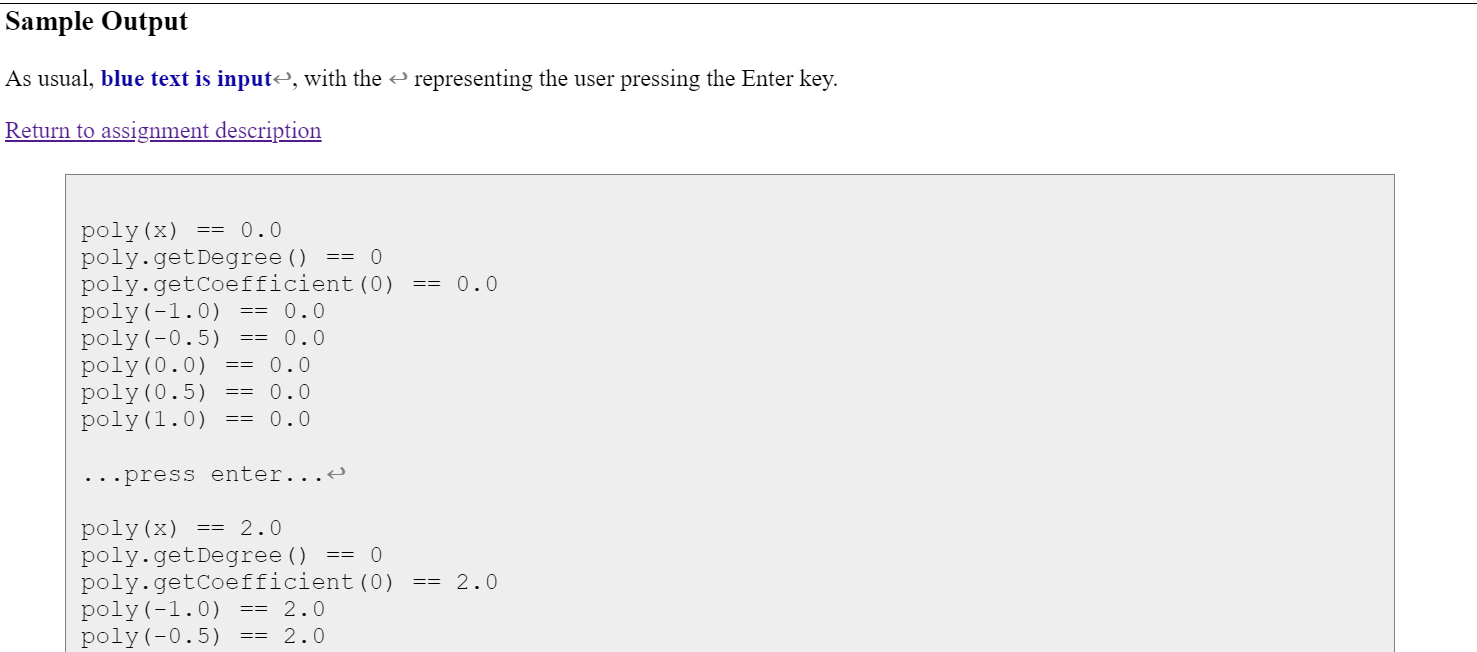
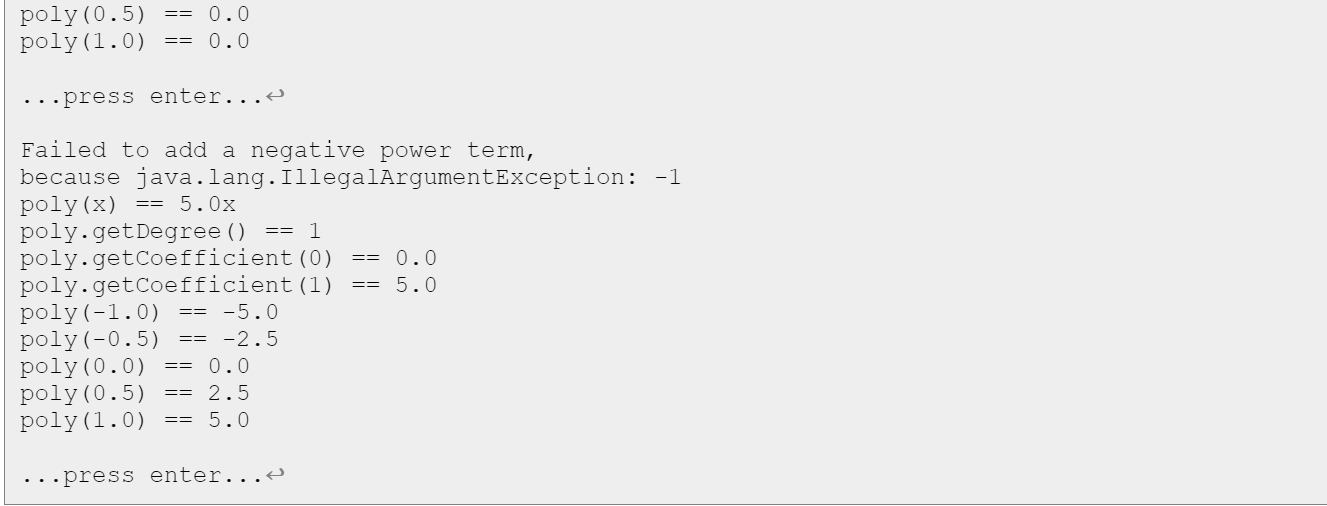
  As usual, blue text is input , with the  representing the user pressing the Enter key. Return to assignment description poly (x)==0.0 poly.getDegree ()==0 poly.getcoefficient (0)==0.0 poly (1.0)==0.0 poly (0.5)==0.0 poly (0.0)==0.0 poly (0.5)==0.0 poly (1.0)==0.0 mpres.s enter... poly (x)==2.0 poly.getDegree ()==0 poly.getcoefficient (0)==2.0 poly (1.0)==2.0 poly (0.5)==2.0 poly (0.0)==2.0 poly (0.5)==2.0 poly (1.0)==2.0  press enter... poly(x)== 3.5x+2.0 poly.getdegree ()==1 poly.getcoefficient (0)==2.0 poly.getcoefficient (1)==3.5 poly (1.0)==1.5 poly (0.5)==0.25 poly (0.0)==2.0 poly (0.5)==3.75 poly(1.0) ==5.5 poly (0.5)==0.4937499999999999 poly (0.0)==2.0 poly (0.5)==4.00625 poly (1.0)==6.7 Mpress enter... poly (x)==0.2x5+5.1x3+x2+3.5x+2.0 poly.getDegree ()==5 poly.getcoefficient (0)==2.0 poly.getcoefficient (1)==3.5 poly.getcoefficient (2)==1.0 poly.getcoefficient (3)==5.1 poly.getcoefficient (4)==0.0 poly.getcoefficient (5)==0.2 poly (1.0)==4.3999999999999995 poly (0.5)==1.13125 poly (0.0)==2.0 poly (0.5)==3.36875 poly (1.0)==1.6000000000000005 .press enter... poly (x)==3.2x5+5.1x3+x2+3.5x+2.0 poly.getDegree ()==5 poly.getcoefficient (0) ==2.0 poly.getcoefficient (1)==3.5 poly.getcoefficient (2)==1.0 poly.getcoefficient (3)==5.1 poly.getcoefficient (4) ==0.0 poly.getcoefficient (5) ==3.2 poly (1.0)==0.39999999999999947 poly (0.5)==0.7875000000000001 poly (0.0)==2.0 poly (0.5)==3.2125 poly (1.0)==3.6000000000000005 Mress enter... poly (x)==0.0 poly.getDegree ()==0 poly.getcoefficient (0) ==0.0 poly (1.0)==0.0 poly (0.5)==0.0 poly (0.0)==0.0 poly (0.5)==0.0 poly (1.0)==0.0 Mpress enter... Failed to add a negative power term, because java.lang.IllegalArgumentException: 1 poly (x)==5.0x poly.getdegree ()==1 poly.getcoefficient (0)==0.0 poly.getcoefficient (1)==5.0 poly (1.0)==5.0 poly (0.5)==2.5 poly (0.0)==0.0 poly (0.5)==2.5 poly (1.0)==5.0 Wres. =0