Please see Question #4 below. I'm not sure how to do it?! and I need help to solve this question. I have also provided examples, that I'm hoping to be helpful- it has to be through Excel. please help!!
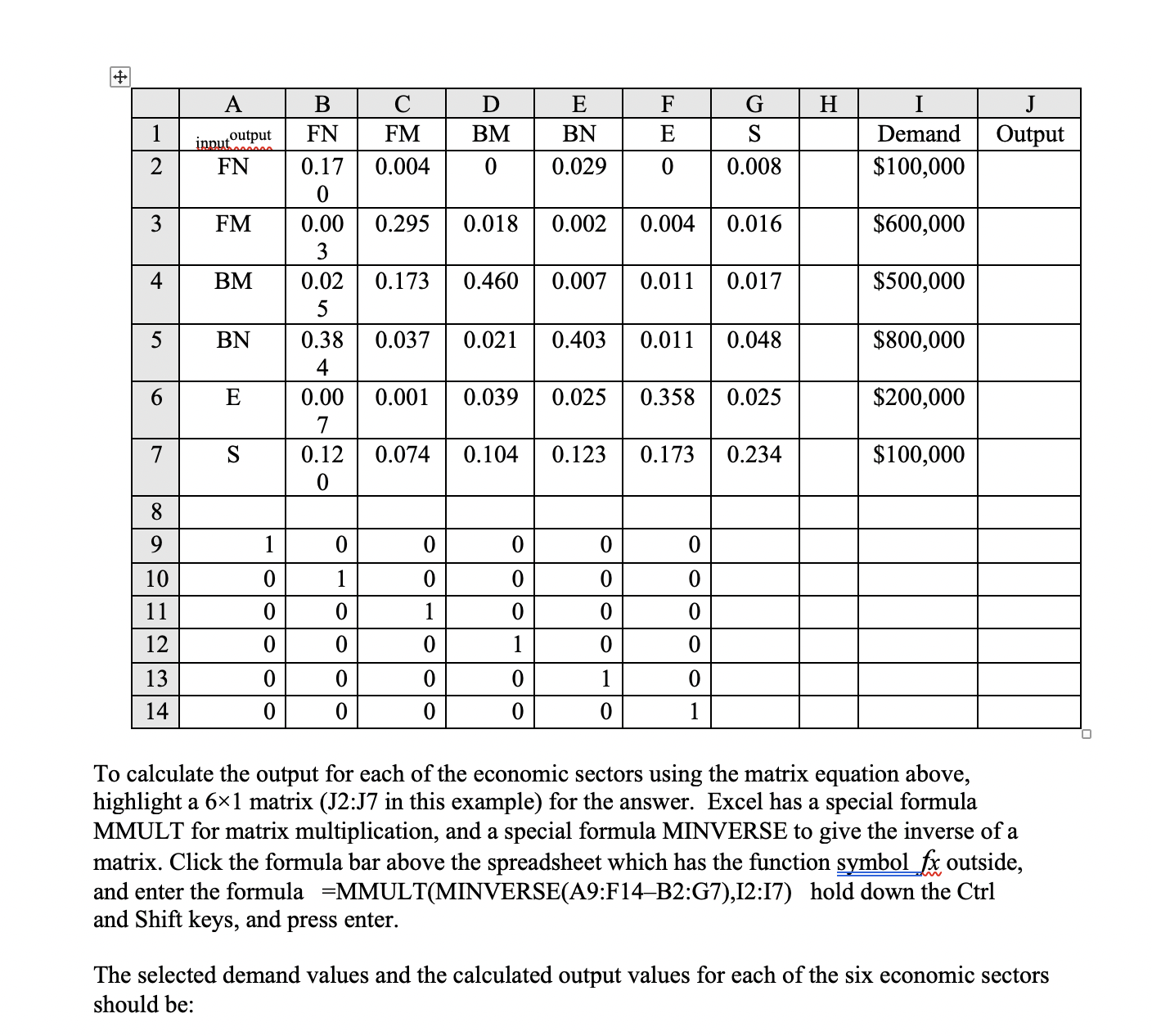
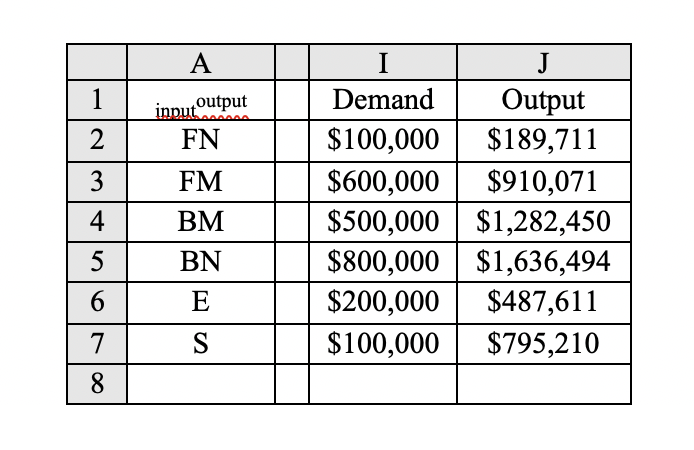
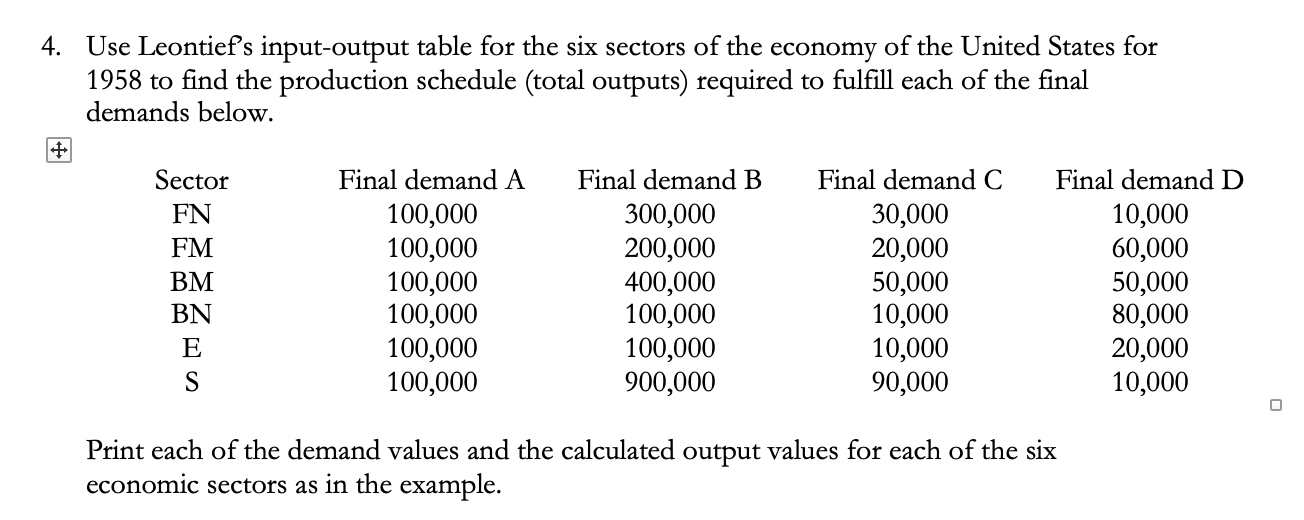
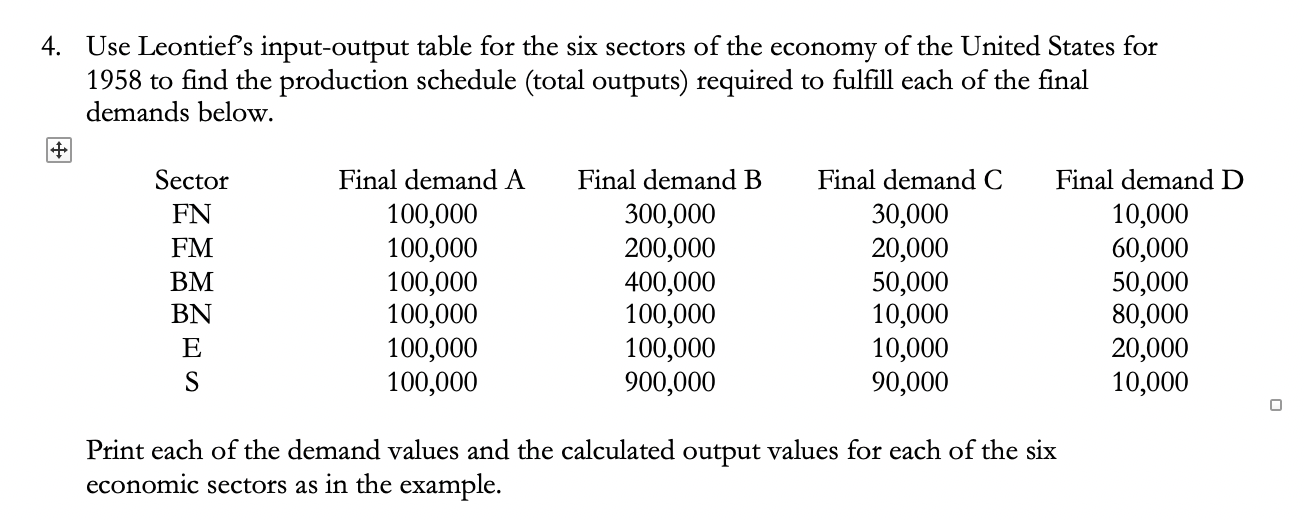
A B C D E F G H J inputoutput FN FM BM BN E S Demand Output 2 FN 0.17 0.004 0 0.029 0 0.008 $100,000 3 FM 0.00 0.295 0.018 0.002 0.004 0.016 $600,000 3 4 BM 0.02 0.173 0.460 0.007 0.011 0.017 $500,000 5 5 BN 0.38 0.037 0.021 0.403 0.011 0.048 $800,000 4 6 E 0.00 0.001 0.039 0.025 0.358 0.025 $200,000 7 7 S 0.12 0.074 0.104 0.123 0.173 0.234 $100,000 0 8 9 0 10 0 1 0 11 0 0 0 12 0 0 0 o o O O 13 0 0 0 0 0 14 0 0 0 0 0 To calculate the output for each of the economic sectors using the matrix equation above, highlight a 6x1 matrix (J2:J7 in this example) for the answer. Excel has a special formula MMULT for matrix multiplication, and a special formula MINVERSE to give the inverse of a matrix. Click the formula bar above the spreadsheet which has the function symbol fx outside, and enter the formula =MMULT(MINVERSE(A9:F14-B2:G7),12:17) hold down the Ctrl and Shift keys, and press enter. The selected demand values and the calculated output values for each of the six economic sectors should be:\fThe following table is a 6X6 technology matrix that gives Leontief's input-output ihterdependence for the six sectors of the economy. For m the value 0018 in the FM row and the BM column means that $0.018 of nal metal is needed as input to produce $1 worth of basic metal output. to produce $1 worth of output _____ E mu- 0 029 0008 0-004 0016 0.011 0.017 0.011 0.048 mm Because there are many economic sectors not included in this model, the columns do not add to a full dollars' worth of output. If this table is written as a 6 X 6 matrix A being technology matrix and the production matrix P and the supply matrix S are each 6 X 1 matrices, then S = A x P. This is similar to saying that the input is a percent of the output. Substituting (A x P) for matrix D previous equation above, yields P (A P) = D. Factoring out the output matrix gives P x (I A) = D. Multiplying both sides by the inverse of (I A) solves for the production P=(IA)'1 x D. Example 3: Use Excel to nd the production/output of the U.S. 1958 economic input-output system. Enter the data for the technology matrix (cells B2267), a desired surplus matrix (cells 12:17) entered as numbers but formatted as currency, and a 6X6 identity matrix (cells A9:El4). Also enter a place to calculate the output (cells J22J7) also formatted as currency. Use an Excel Spreadsheet to Work Leontief Input-Output Model Economist Wassily W. Leontief (1906 - 1999) was born in Saint Petersburg, Russia. He enrolled at Leningrad University at the age of M graduated ve years later with the title of \"Learned Economist.\" Two year after that he earned his Ph.D. and immigrated to the United States to join the National Bureau of Economic Research in New York City. In 1931 he began his 35-year tenure as a member of the faculty of Harvard University. Leontiefs Nobel Prize in economics (1973) cited him for his creation of the input-output technique. He defined input as the goods and services that each industry buys from all the other industries, and output as the product an industry sells to the others. By this method, the variations in the ow of goods 'om one industry to another can be graphically demonstrated using matrices. Economists use his method to analyze, plan, and predict economic changes. Input-output analysis began in the 1920's when the federal government organized data to get a clearer picture of its economy. As a young professor at Harvard, Leontief developed the primary methods of input-output analysis that later were instrumental in the important Controlled Materials Plan during World War II. After World War H, the Air Force and the Department of Labor funded a project called Project Scoop, which provided a detailed analysis of the economy. Since then, input-output analysis has been regarded as one of the cornerstones of economic theory. In 1965 Leontief published an account of the US. economy based on the statistics from 1958. His analysis examined the interdependence among 81 industrial sectors. A modest version is presented here in which the industries are lumped together into six sectors. The following table lists the sectors and some representative industries from each. Although it includes many items in our everyday lives, obviously it does not cover everything. Government and construction are two large sectors not included here. Abbreviation Re u resentative industries Final nonmetal A. .arel, food, dru_s, furniture Final metal Motor vehicles, aircraft, communications Livestock, agriculture products, fabrics, lumber Electrici , as, water, coal, etroleum Trans: ortation, insurance, real estate, nance The total output (production P) of these sectors equals the input (supply S) in the relationship plus the demand D of the rest of the economy: Basic nonmetal Enera Services Basic metal P=S+DorPS=D 4. Use Leontief's input-output table for the six sectors of the economy of the United States for 1958 to find the production schedule (total outputs) required to fulfill each of the final demands below. Sector Final demand A Final demand B Final demand C Final demand D FN 100,000 300,000 30,000 10,000 FM 100,000 200,000 20,000 60,000 BM 100,000 400,000 50,000 50,000 BN 100,000 100,000 10,000 80,000 E 100,000 100,000 10,000 20,000 100,000 900,000 90,000 10,000 Print each of the demand values and the calculated output values for each of the six economic sectors as in the example