Please see questions in photos attached (Please this question doesn't violate any form of honors code)
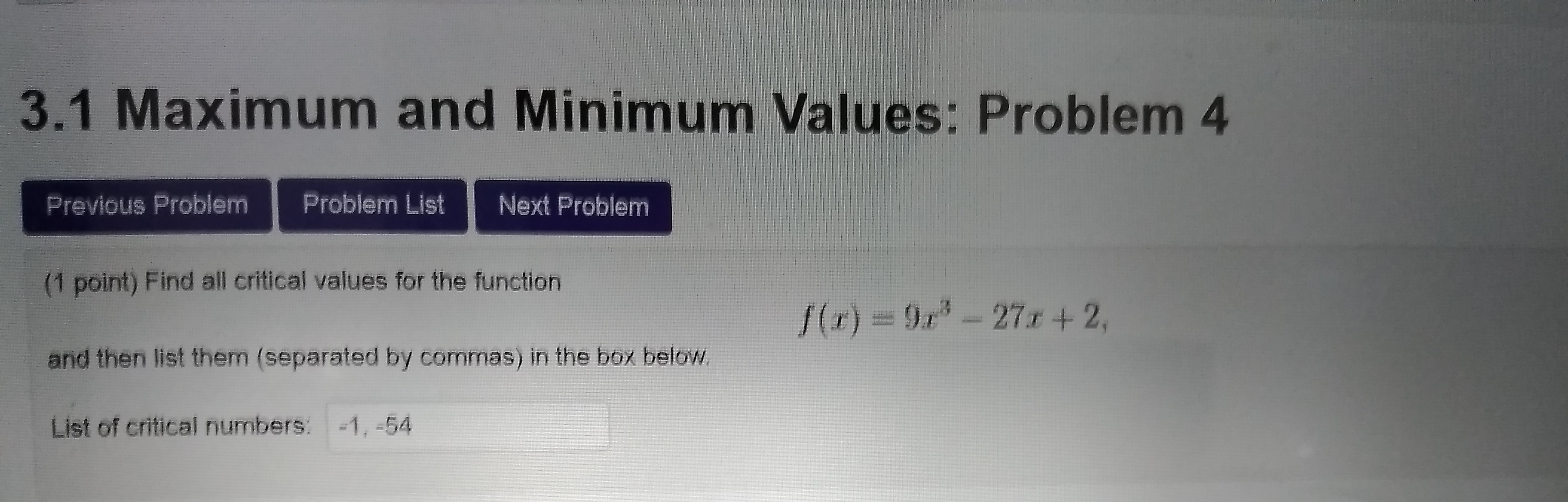
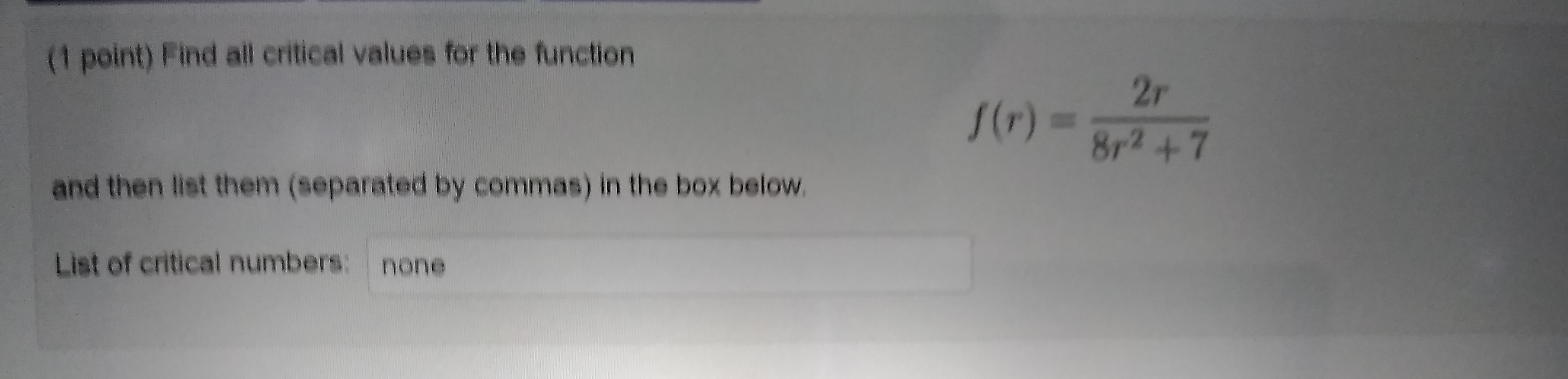
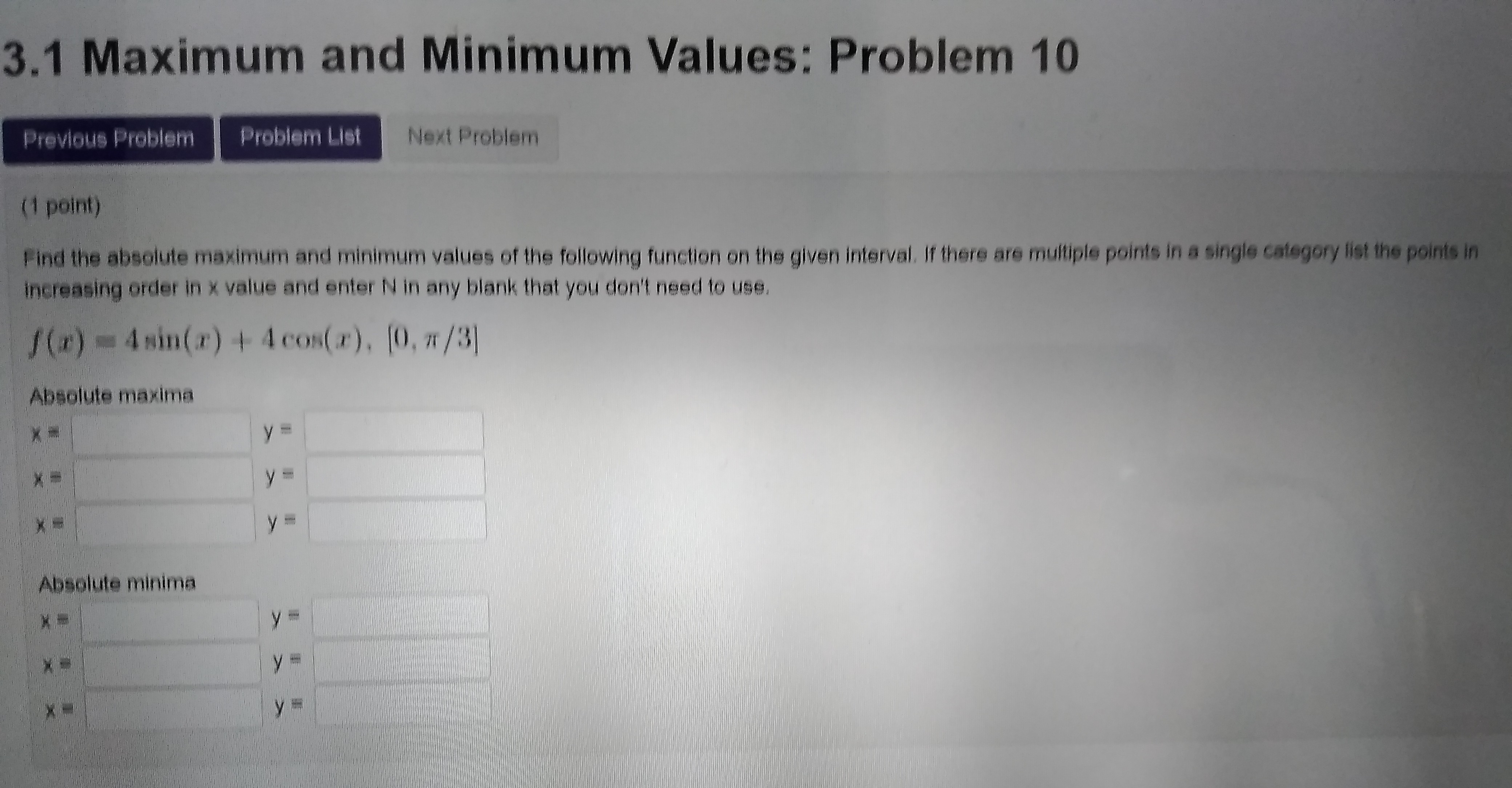
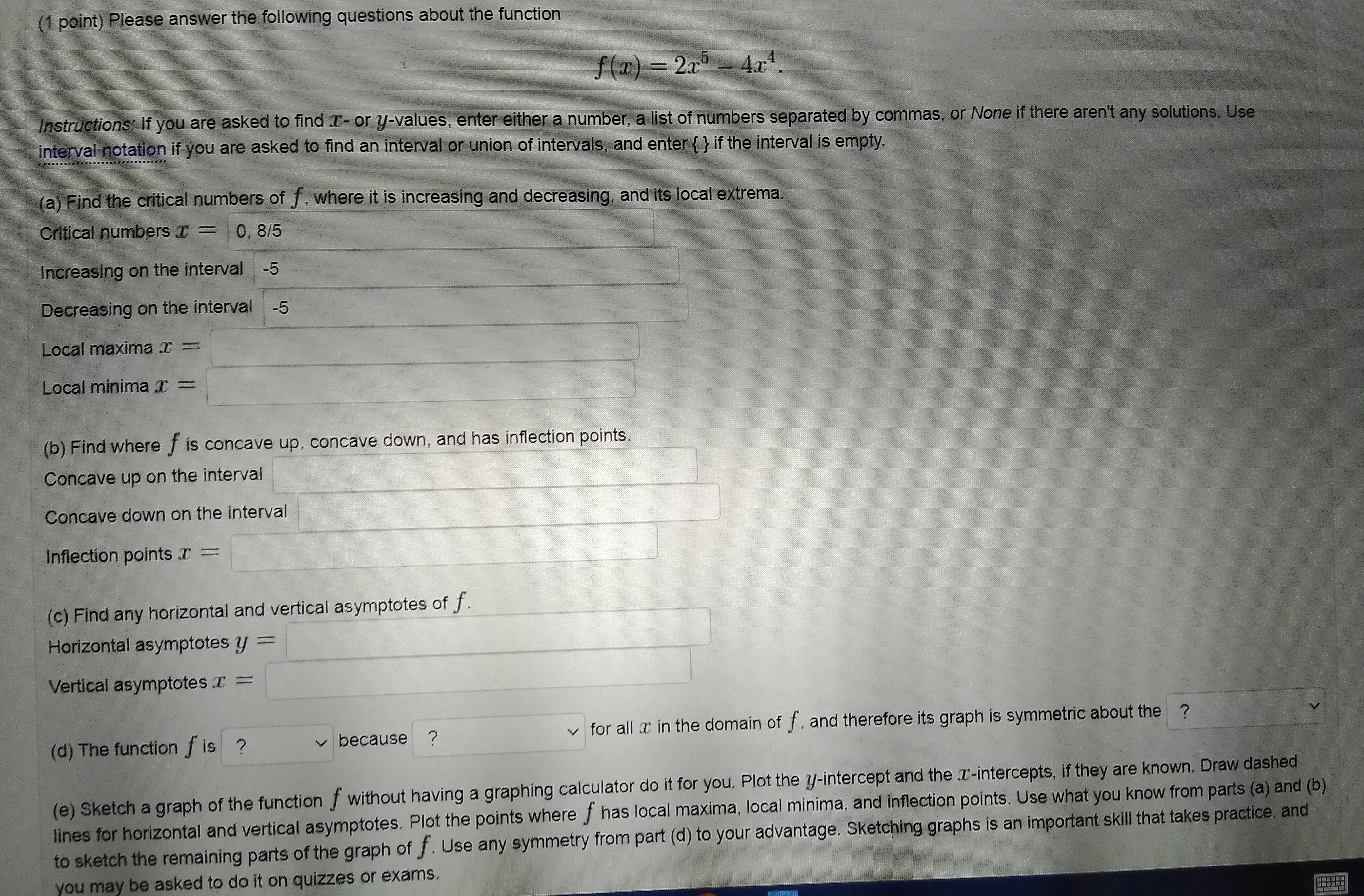
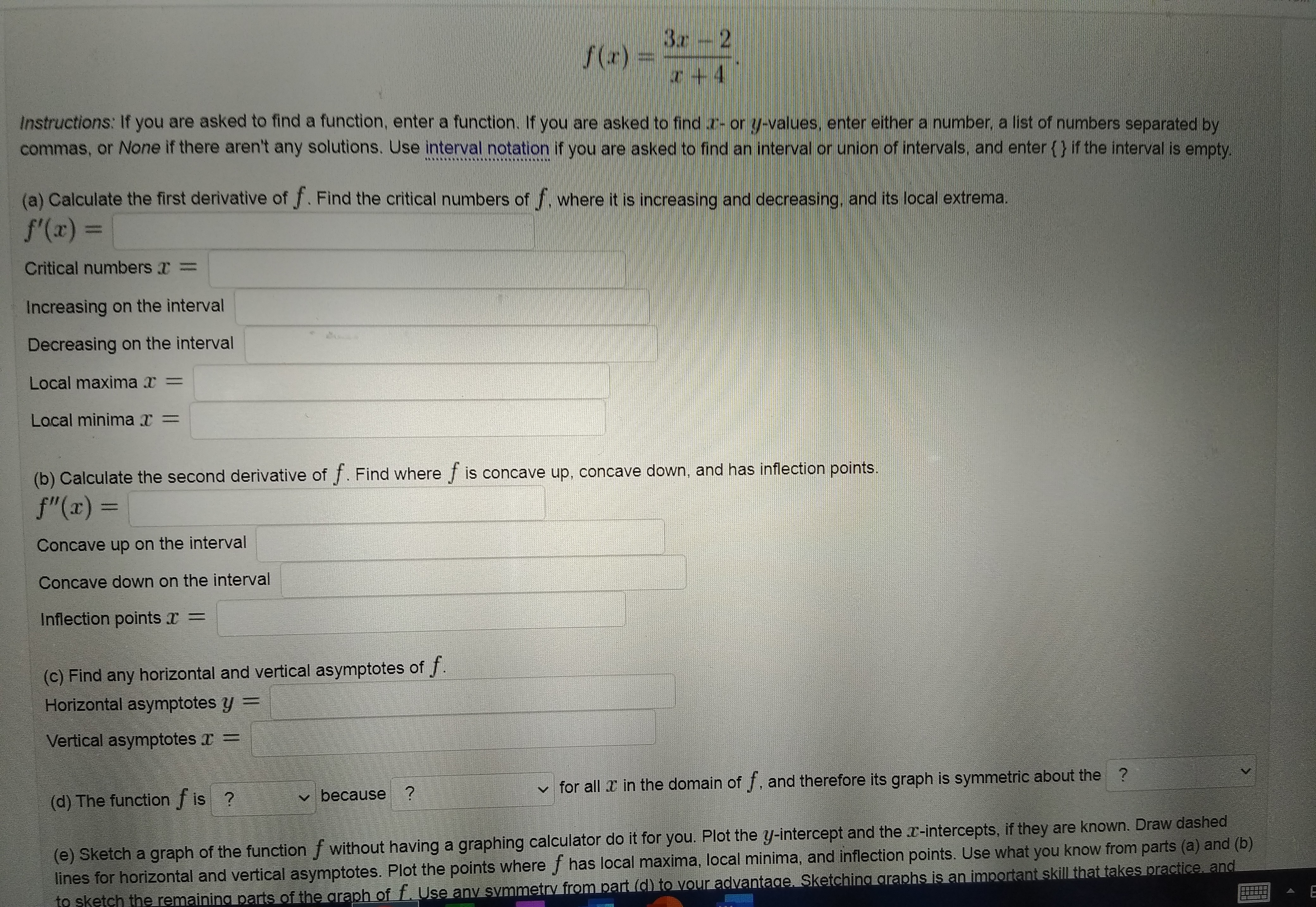
3.1 Maximum and Minimum Values: Problem 4 Previous Problem Problem List Next Problem (1 point) Find all critical values for the function f(x) = 913 - 27x+ 2, and then list them (separated by commas) in the box below. List of critical numbers: -1, -54(1 point) Find all critical values for the function 1 (r) = 2r 812 +7 and then list them (separated by commas) in the box below, List of critical numbers: none3.1 Maximum and Minimum Values: Problem 10 Previous Problem Problem List Next Problem (1 point) Find the absolute maximum and minimum values of the following function on the given interval. If there are multiple points in a single category list the points in increasing order in x value and enter N in any blank that you don't need to use. f(*) = 4min(x) 4 4 cos(x), [0, 7/3) Absolute maxima Absolute minima(1 point) Please answer the following questions about the function f(x) = 215 - 4.+. Instructions: If you are asked to find a- or y-values, enter either a number, a list of numbers separated by commas, or None if there aren't any solutions. Use interval notation if you are asked to find an interval or union of intervals, and enter { } if the interval is empty. (a) Find the critical numbers of f, where it is increasing and decreasing, and its local extrema. Critical numbers I = 0, 8/5 Increasing on the interval -5 Decreasing on the interval -5 Local maxima T = Local minima T = (b) Find where f is concave up, concave down, and has inflection points. Concave up on the interval Concave down on the interval Inflection points _ = (c) Find any horizontal and vertical asymptotes of f. Horizontal asymptotes y = Vertical asymptotes _ = (d) The function f is ? because ? for all i in the domain of f, and therefore its graph is symmetric about the ? (e) Sketch a graph of the function f without having a graphing calculator do it for you. Plot the y-intercept and the I-intercepts, if they are known. Draw dashed lines for horizontal and vertical asymptotes. Plot the points where } has local maxima, local minima, and inflection points. Use what you know from parts (a) and (b) to sketch the remaining parts of the graph of f. Use any symmetry from part (d) to your advantage. Sketching graphs is an important skill that takes practice, and you may be asked to do it on quizzes or exams.Instructions: If you are asked to find a function, enter a function. If you are asked to find ."- or /-values, enter either a number, a list of numbers separated by commas, or None if there aren't any solutions. Use interval notation if you are asked to find an interval or union of intervals, and enter { } if the interval is empty f'(x) = (a) Calculate the first derivative of f . Find the critical numbers of f, where it is increasing and decreasing, and its local extrema. Critical numbers T = Increasing on the interval Decreasing on the interval Local maxima _ = Local minima T (b) Calculate the second derivative of f . Find where f is concave up, concave down, and has inflection points. f"(x) = Concave up on the interval Concave down on the interval Inflection points T = (c) Find any horizontal and vertical asymptotes of f. Horizontal asymptotes y = Vertical asymptotes T = (d) The function f is ? because ? for all T in the domain of f, and therefore its graph is symmetric about the ? e) Sketch a graph of the function f without having a graphing calculator do it for you. Plot the y-intercept and the T-intercepts, if they are known. Draw dashed lines for horizontal and vertical asymptotes. Plot the points where / has local maxima, local minima, and inflection points. Use what you know from parts (a) and (b) to sketch the remaining parts of the graph of f. Use any symmetry from part (d) to your advantage. Sketching graphs is an important skill that takes practice, and