Please show all information
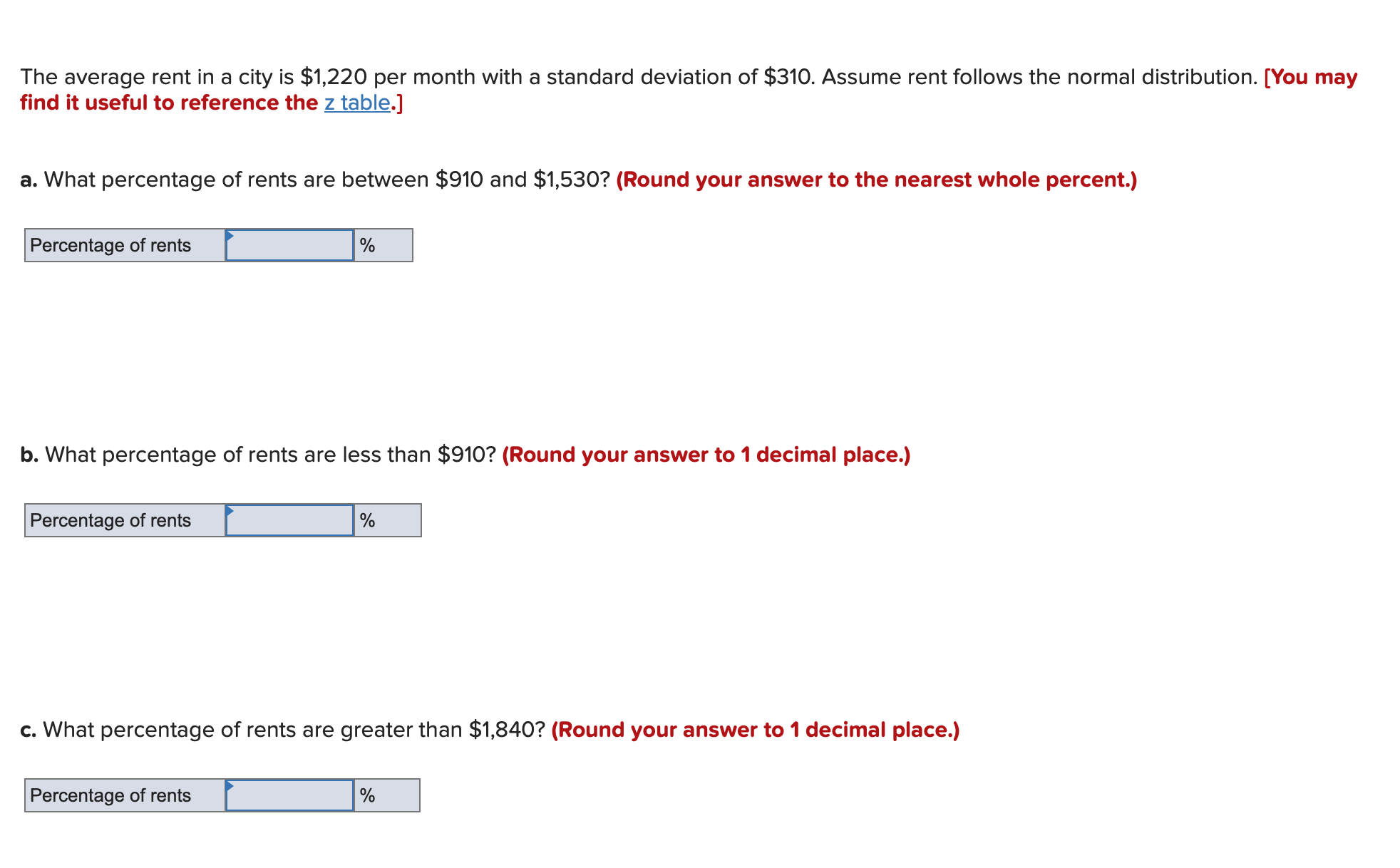
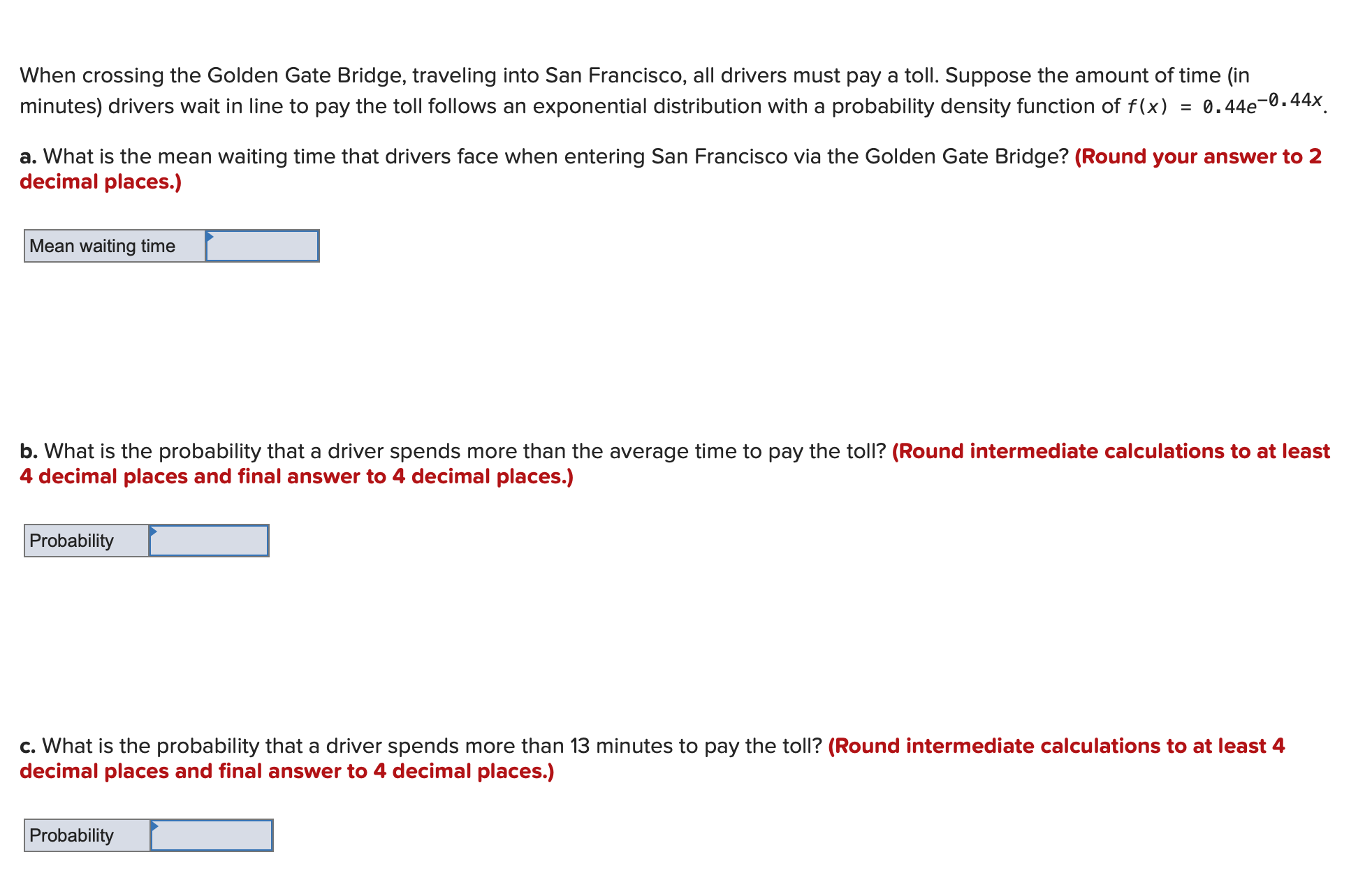
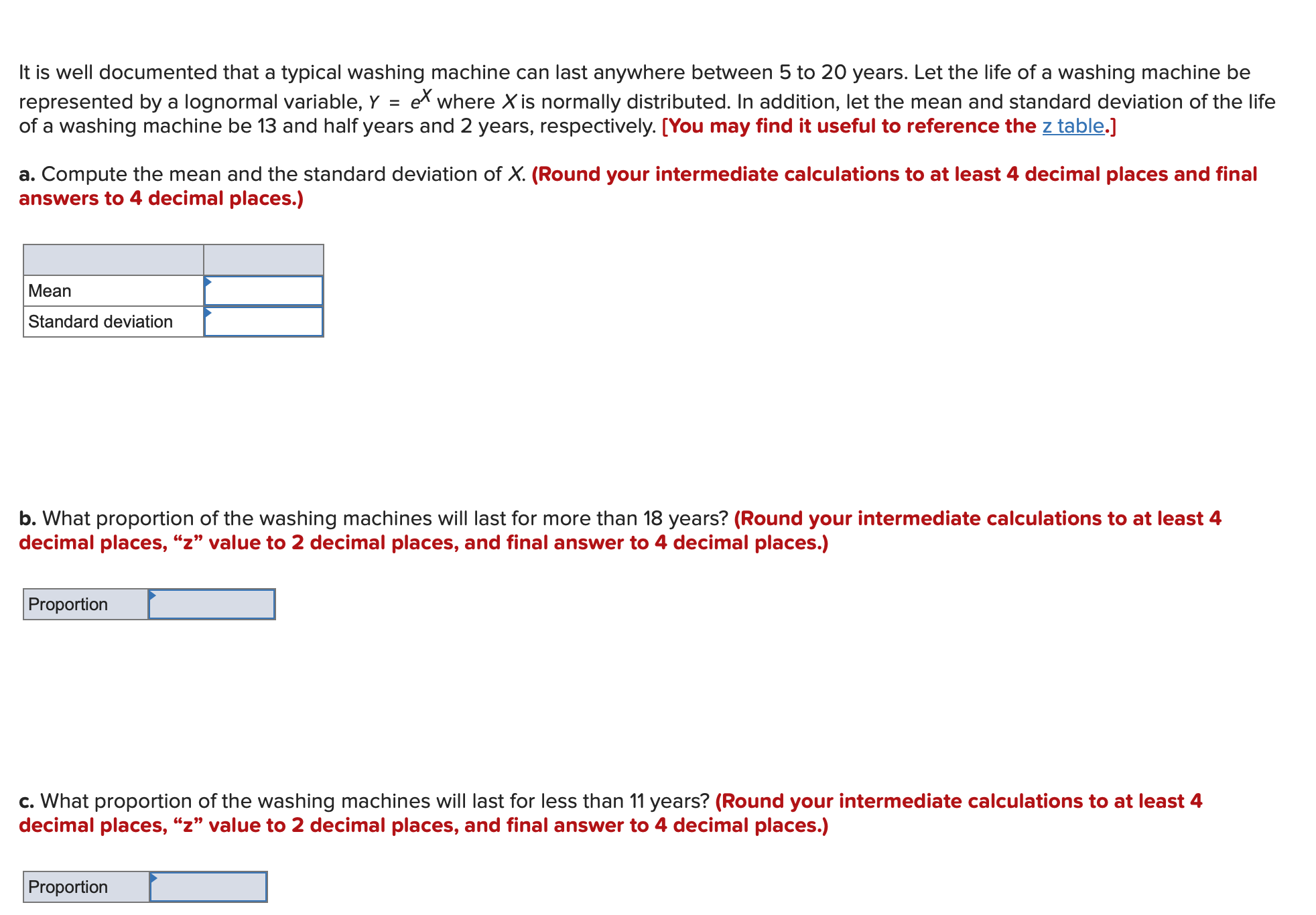
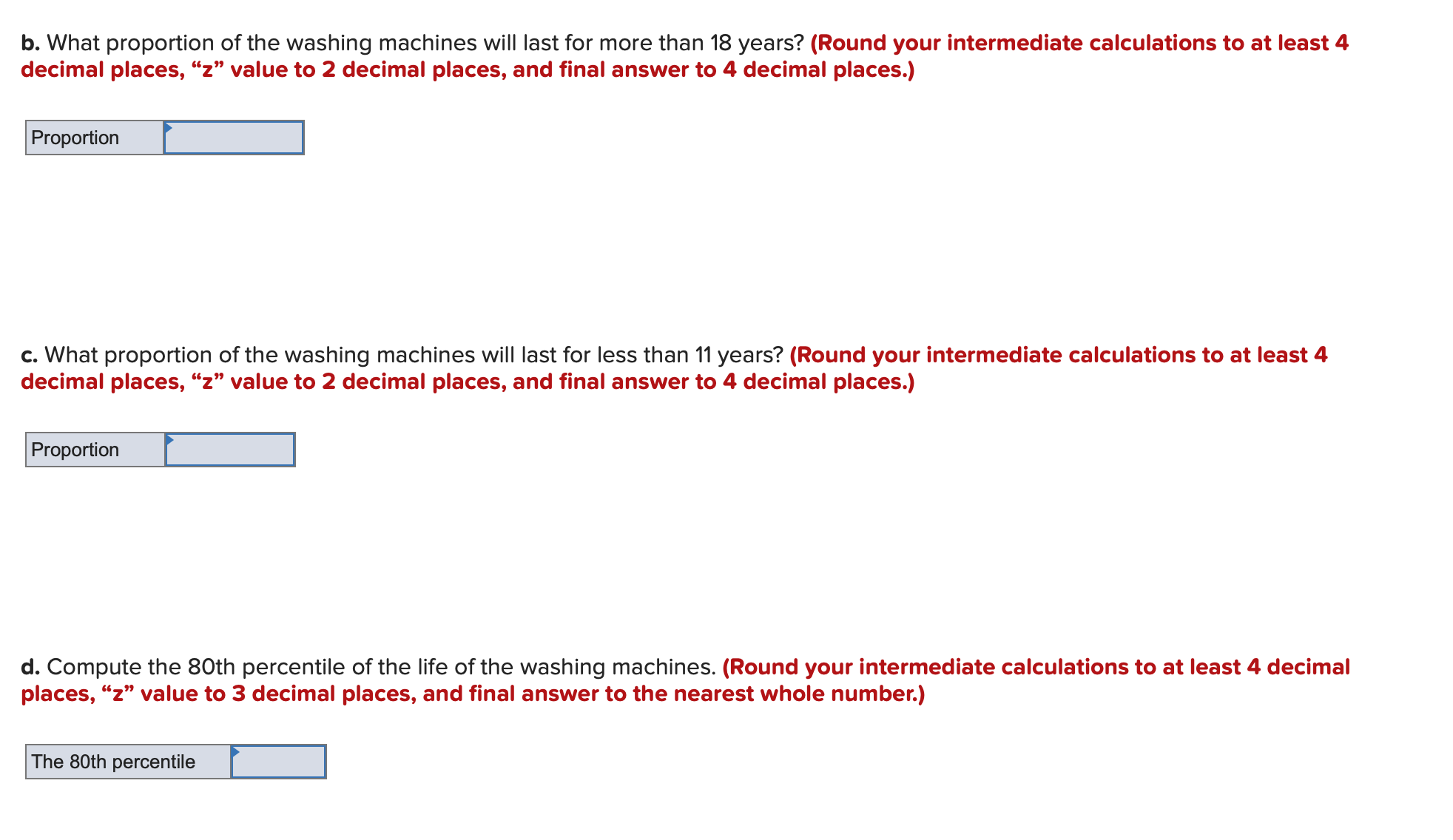
For a continuous random variable X, P(21 5 X5 61) = 0.31 and P(X> 61) = 0.21. Calculate the following probabilities. (Leave no cells blank - be certain to enter "0" wherever required. Round your answers to 2 decimal places.) a. P(X 0.67) b P(Z S -1.58) C. P(0 S Z S 1.4) d. P(-0.79 s Z s 2.49)The average rent in a city is $1,220 per month with a standard deviation of $310. Assume rent follows the normal distribution. [You may find it useful to reference the 2 table.] a. What percentage of rents are between $910 and $1,530? (Round your answer to the nearest whole percent.) Percentage of rents _ % b. What percentage of rents are less than $910? {Round your answer to 1 decimal place.) Percentage of rents - % c. What percentage of rents are greater than $1,840? (Round your answer to 1 decimal place.) Percentage of rents - % When crossing the Golden Gate Bridge, traveling into San Francisco, all drivers must pay a toll. Suppose the amount of time (in minutes) drivers wait in line to pay the toll follows an exponential distribution with a probability density function of f(x) = 0.44e'0-44". a. What is the mean waiting time that drivers face when entering San Francisco via the Golden Gate Bridge? (Round your answer to 2 decimal places.) Mean waiting time - b. What is the probability that a driver spends more than the average time to pay the toll? (Round intermediate calculations to at least 4 decimal places and nal answer to 4 decimal places.) Probability E | c. What is the probability that a driver spends more than 13 minutes to pay the toll? (Round intermediate calculations to at least 4 decimal places and final answer to 4 decimal places.) Probability _ It is well documented that a typical washing machine can last anywhere between 5 to 20 years. Let the life ofa washing machine be represented by a lognormal variable, Y = ethere Xis normally distributed, In addition, let the mean and standard deviation of the life of a washing machine be 13 and half years and 2 years, respectively. [You may find it useful to reference the 2 table.] a. Compute the mean and the standard deviation of X. (Round your intermediate calculations to at least 4 decimal places and nal answers to 4 decimal places.) Mean Standard deviation b. What proportion of the washing machines will last for more than 18 years? (Round your intermediate calculations to at least 4 decimal places, \"2" value to 2 decimal places, and final answer to 4 decimal places.) c. What proportion of the washing machines will last for less than 11 years? (Round your intermediate calculations to at least 4 decimal places, \"2" value to 2 decimal places, and final answer to 4 decimal places.) b. What proportion of the washing machines will last for more than 18 years? (Round your intermediate calculations to at least 4 decimal places, \"2" value to 2 decimal places, and final answer to 4 decimal places.) c. What proportion of the washing machines will last for less than 11 years? (Round your intermediate calculations to at least 4 decimal places, \"2" value to 2 decimal places, and final answer to 4 decimal places.) d. Compute the 80th percentile of the life of the washing machines. (Round your intermediate calculations to at least 4 decimal places, \"2\" value to 3 decimal places, and final answer to the nearest whole number.) The 80th percentile I I A random variable Xfollows the uniform distribution with a lower limit of 620 and an upper limit of 820. a. Calculate the mean and the standard deviation for the distribution. (Round intermediate calculation for standard deviation to 4 decimal places and final answer to 2 decimal places.) Mean Standard deviation b. What is the probability that X is less than 750? (Round intermediate calculations to at least 4 decimal places and final answer to 2 decimal places.) Probability [ | Let X be normally distributed with mean / = 2.9 and standard deviation o= 1.5. [You may find it useful to reference the z table.] a. Find P(X > 6.5). (Round "z" value to 2 decimal places and final answer to 4 decimal places.) P(X > 6.5) b. Find P(5.5 s X $7.5). (Round "z" value to 2 decimal places and final answer to 4 decimal places.) P(5.5 s X S 7.5) c. Find x such that P(X > x) = 0.0594. (Round "z" value and final answer to 3 decimal places.) Xd. Find X such that P(x 5 X5 2.9) = 0.4066. (Negative value should be indicated by a minus sign. Round "2" value and final answer to 3 decimal places.) E: d. What is the probability that a driver spends between 5 and 9 minutes to pay the toll? (Round intermediate calculations to at least 4 decimal places and final answer to 4 decimal places.)