Please Show All Work

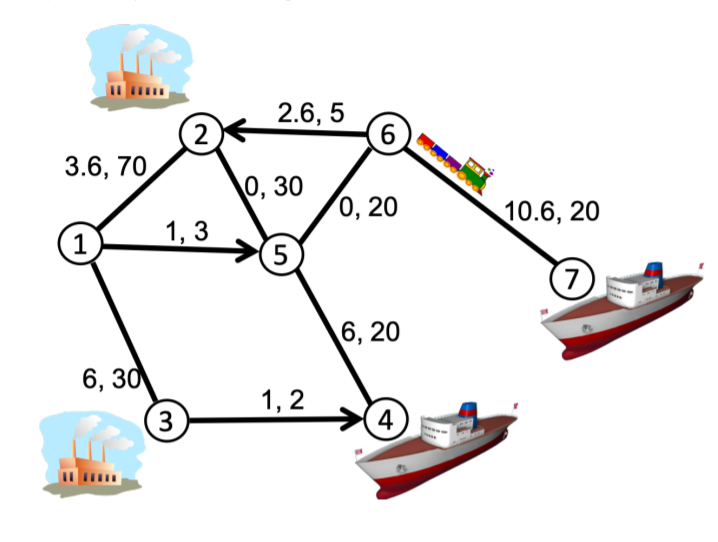
2.6.5 2. 6 3.6, 70 10, 30 0, 20 (10.6, 20 1 1,3 5 7 16, 20 6, 30 1,2 3 4 1. In the following network of railroads, some railroads are one-way and some are two-way railroads. There are factories at vertex #2 and #3 which make cars. Each factory has 8 cars that need to be shipped out. There is a ship with room for 6 cars waiting at the harbor at vertex #7, and a bigger ship with room for 10 cars waiting at a different harbor at vertex #4. The shipping cost (per car) and capacity of each railroad segment is given as "cost, capacity". Our goal is to transport all the cars to the waiting ships at the smallest possible cost. a) formulate this problem as a linear program b) Of course, you can only ship an integer-valued number of cars on each railroad. Is it true that the linear programming problem in part (a) must have an integer-valued optimal solution? Or do we need to add constraints that say that the variables must be integer-valued? Please explain. c) Find the optimal solution using MATLAB. 2. In the same network as problem #1, you just upgraded each of the two factories so that they now each have 20 cars ready to ship out! However, the two boats still have room for the same number of cars as before. Your goal is now to transport, at the minimum possible cost, just some of the cars from the two factories in order to fill the two boats up so that they are carrying as many cars as possible. a) formulate this problem as a linear program b) find the optimal solution on MATLAB 2.6.5 2. 6 3.6, 70 10, 30 0, 20 (10.6, 20 1 1,3 5 7 16, 20 6, 30 1,2 3 4 1. In the following network of railroads, some railroads are one-way and some are two-way railroads. There are factories at vertex #2 and #3 which make cars. Each factory has 8 cars that need to be shipped out. There is a ship with room for 6 cars waiting at the harbor at vertex #7, and a bigger ship with room for 10 cars waiting at a different harbor at vertex #4. The shipping cost (per car) and capacity of each railroad segment is given as "cost, capacity". Our goal is to transport all the cars to the waiting ships at the smallest possible cost. a) formulate this problem as a linear program b) Of course, you can only ship an integer-valued number of cars on each railroad. Is it true that the linear programming problem in part (a) must have an integer-valued optimal solution? Or do we need to add constraints that say that the variables must be integer-valued? Please explain. c) Find the optimal solution using MATLAB. 2. In the same network as problem #1, you just upgraded each of the two factories so that they now each have 20 cars ready to ship out! However, the two boats still have room for the same number of cars as before. Your goal is now to transport, at the minimum possible cost, just some of the cars from the two factories in order to fill the two boats up so that they are carrying as many cars as possible. a) formulate this problem as a linear program b) find the optimal solution on MATLAB