Please show the solution in Excel step-by-step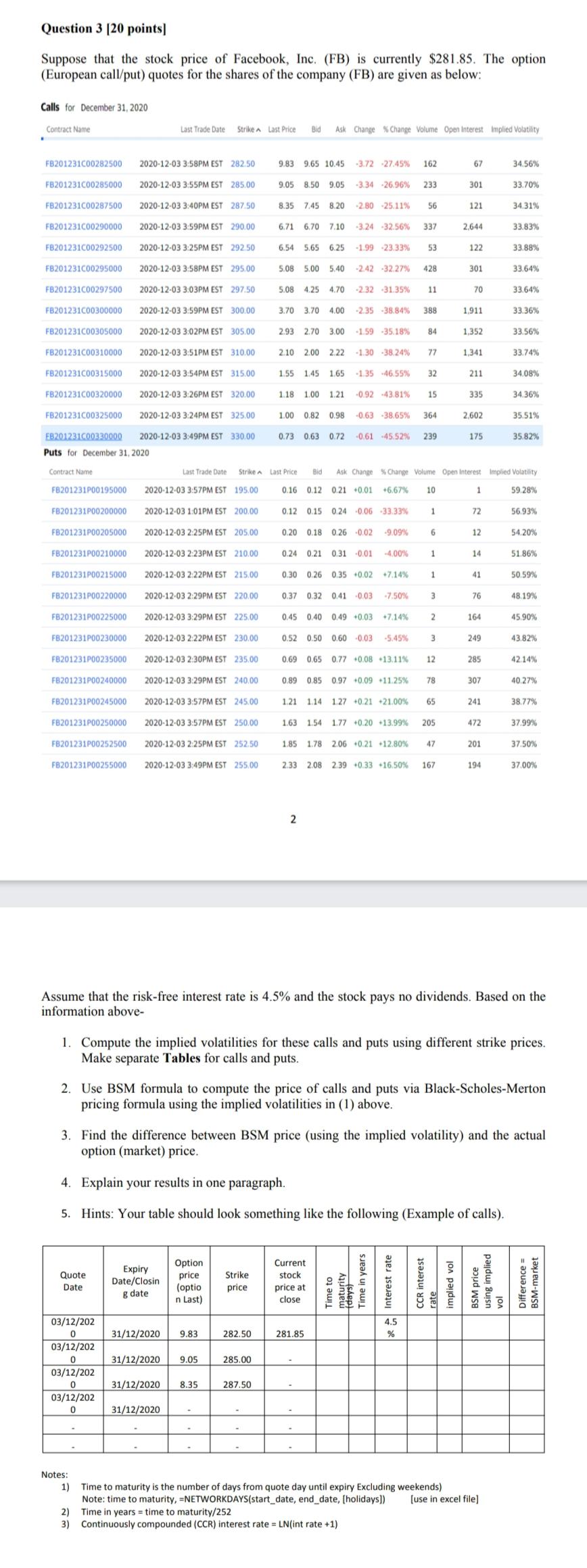
Question 3 (20 points) Suppose that the stock price of Facebook, Inc. (FB) is currently $281.85. The option (European call/put) quotes for the shares of the company (FB) are given as below: Calls for December 31, 2020 Contract Name Last Trade Date Strike A Last Price Bid Ask Change Change Volume Open Interest Implied Volatility FB201231C00282500 2020-12-03 3:58PM EST 282.50 9.83 9.65 10.45 -3.72 27.45% 162 67 34.56% FB201231C00285000 2020-12-03 3:55PM EST 285.00 9.05 8.50 9.05 -3.34 26.96% 233 301 33.70% FB201231C00287500 2020-12-03 3:40PM EST 287.50 8.35 7.45 8.20 -2.80 25.11% 56 121 34.31% FB201231C00290000 2020-12-03 3:59PM EST 290.00 6.71 6.70 7.10 -3.24 -32.56% 337 2.644 33.83% FB201231C00292500 2020-12.03 3:25PM EST 292.50 6.54 5.65 6.25 -1.99 23.33% 53 122 33.88% FB201231C00295000 2020-12-03 3:58PM EST 295.00 5.08 5.00 5.40 -2.42 -32.27% 428 301 33.64% FB201231C00297500 2020-12.03 3:03PM EST 297.50 5.08 4.25 4.70 -2.32 31.35% 11 70 33.64% FB201231C00300000 2020-12-03 3:59PM EST 300.00 3.70 3.70 4.00 -2.35 -38.84% 388 1.911 33.36% FB201231C00305000 2020-12-03 3:02PM EST 305.00 2.93 2.70 3.00 -1.59-35.18% 84 1,352 33.56% FB201231C00310000 2020-12-03 3:51PM EST 310.00 2.10 2.00 2.22 -1.30 -38.24% 77 1.341 33.74% FB201231C00315000 2020-12-03 3:54PM EST 315.00 1.55 145 1.65 -1.35 46.55% 32 211 34,08% FB201231C00320000 2020-12-03 3:26PM EST 320.00 1.18 1.00 1.21 -0.92.43.81% 15 335 34.36% FB201231000325000 2020-12-03 3:24PM EST 325.00 1.00 0.82 0.98 -0.63 38.65% 364 2,602 35.51% 0.73 0.63 0.72 -0.61 -45.52% 239 175 35.82% FB201231C00330000 2020-12-03 3:49PM EST 330.00 Puts for December 31, 2020 Contract Name Last Trade Date Strike Last Price Bid Ask Change % Change Volume Open Interest Implied Volatility FB201231P00195000 2020-12-03 3:57PM EST 195.00 0.16 0.12 0.21 0.01 +6.67% 10 1 59.28% FB201231P00200000 2020-12-03 1:01PM EST 200.00 0.12 0.15 0.24 0.06 -33.33% 1 72 56.93% FB201231P00205000 2020-12-03 2:25PM EST 205.00 0.20 0.18 0.26 -0.02 9.09% 6 12 54,20% FB201231P00210000 2020-12-03 2:23PM EST 210.00 0.24 0.21 0.31 0.01 -4,00% 1 14 51.86% FB201231P00215000 2020-12-03 2:22PM EST 215.00 0.30 0.26 0.35 0.02 +7.14% 1 41 50.59% FB201231P00220000 2020-12-03 229PM EST 220.00 0.37 0.32 0.41 0.03 -7.50% 3 76 48.19% FB201231P00225000 2020-12-03 3:29PM EST 225.00 0.45 0.40 0.49 +0.03 *7.14% 2 164 45.90% FB201231P00230000 2020-12-03 2:22PM EST 230.00 0.52 0.50 0.60 0.03 -5.45% 3 249 43.82% FB201231P00235000 2020-12-03 2:30PM EST 235.00 0.69 0.65 0.77 +0.08 13.11% 12 285 42.14% FB201231P00240000 2020-12-03 3:29PM EST 240.00 0.89 0.85 0.97 +0.09-11.25% 78 307 40.27% FB201231P00245000 2020-12-03 3:57PM EST 245.00 1.21 1.14 1.27 +0.21 -21.00% 65 241 38.77% FB201231P00250000 2020-12-03 3:57PM EST 250.00 1.63 1.54 1.77 +0.20 +13.99% 205 472 37.99% FB201231P00252500 2020-12-03 2:25PM EST 252.50 1.85 1.78 2.06 0.21 +12 80% 47 201 37.50% FB201231P00255000 2020-12-03 3:49PM EST 255.00 2.33 2.08 2.39 +0.33 +16,50% 167 194 37.00% 2 Assume that the risk-free interest rate is 4.5% and the stock pays no dividends. Based on the information above- 1. Compute the implied volatilities for these calls and puts using different strike prices. Make separate Tables for calls and puts. 2. Use BSM formula to compute the price of calls and puts via Black-Scholes-Merton pricing formula using the implied volatilities in (1) above. 3. Find the difference between BSM price (using the implied volatility) and the actual option (market) price. 4. Explain your results in one paragraph. 5. Hints: Your table should look something like the following (Example of calls). Quote Date Expiry Date/Closin g date Option price (optio n Last) Strike price Current stock price at close Time to wunder Time in years de Interest rate CCR interest implied vol BSM price using implied vol Difference BSM-market 31/12/2020 9.83 282.50 281.85 31/12/2020 9.05 285.00 03/12/202 0 03/12/202 0 03/12/202 0 03/12/202 0 31/12/2020 8.35 287.50 31/12/2020 Notes: 1) Time to maturity is the number of days from quote day until expiry Excluding weekends) Note: time to maturity, -NETWORKDAYS(start_date, end_date, (holidays]) [use in excel file) 2) Time in years = time to maturity/252 3) Continuously compounded (CCR) interest rate = LN(int rate +1) Question 3 (20 points) Suppose that the stock price of Facebook, Inc. (FB) is currently $281.85. The option (European call/put) quotes for the shares of the company (FB) are given as below: Calls for December 31, 2020 Contract Name Last Trade Date Strike A Last Price Bid Ask Change Change Volume Open Interest Implied Volatility FB201231C00282500 2020-12-03 3:58PM EST 282.50 9.83 9.65 10.45 -3.72 27.45% 162 67 34.56% FB201231C00285000 2020-12-03 3:55PM EST 285.00 9.05 8.50 9.05 -3.34 26.96% 233 301 33.70% FB201231C00287500 2020-12-03 3:40PM EST 287.50 8.35 7.45 8.20 -2.80 25.11% 56 121 34.31% FB201231C00290000 2020-12-03 3:59PM EST 290.00 6.71 6.70 7.10 -3.24 -32.56% 337 2.644 33.83% FB201231C00292500 2020-12.03 3:25PM EST 292.50 6.54 5.65 6.25 -1.99 23.33% 53 122 33.88% FB201231C00295000 2020-12-03 3:58PM EST 295.00 5.08 5.00 5.40 -2.42 -32.27% 428 301 33.64% FB201231C00297500 2020-12.03 3:03PM EST 297.50 5.08 4.25 4.70 -2.32 31.35% 11 70 33.64% FB201231C00300000 2020-12-03 3:59PM EST 300.00 3.70 3.70 4.00 -2.35 -38.84% 388 1.911 33.36% FB201231C00305000 2020-12-03 3:02PM EST 305.00 2.93 2.70 3.00 -1.59-35.18% 84 1,352 33.56% FB201231C00310000 2020-12-03 3:51PM EST 310.00 2.10 2.00 2.22 -1.30 -38.24% 77 1.341 33.74% FB201231C00315000 2020-12-03 3:54PM EST 315.00 1.55 145 1.65 -1.35 46.55% 32 211 34,08% FB201231C00320000 2020-12-03 3:26PM EST 320.00 1.18 1.00 1.21 -0.92.43.81% 15 335 34.36% FB201231000325000 2020-12-03 3:24PM EST 325.00 1.00 0.82 0.98 -0.63 38.65% 364 2,602 35.51% 0.73 0.63 0.72 -0.61 -45.52% 239 175 35.82% FB201231C00330000 2020-12-03 3:49PM EST 330.00 Puts for December 31, 2020 Contract Name Last Trade Date Strike Last Price Bid Ask Change % Change Volume Open Interest Implied Volatility FB201231P00195000 2020-12-03 3:57PM EST 195.00 0.16 0.12 0.21 0.01 +6.67% 10 1 59.28% FB201231P00200000 2020-12-03 1:01PM EST 200.00 0.12 0.15 0.24 0.06 -33.33% 1 72 56.93% FB201231P00205000 2020-12-03 2:25PM EST 205.00 0.20 0.18 0.26 -0.02 9.09% 6 12 54,20% FB201231P00210000 2020-12-03 2:23PM EST 210.00 0.24 0.21 0.31 0.01 -4,00% 1 14 51.86% FB201231P00215000 2020-12-03 2:22PM EST 215.00 0.30 0.26 0.35 0.02 +7.14% 1 41 50.59% FB201231P00220000 2020-12-03 229PM EST 220.00 0.37 0.32 0.41 0.03 -7.50% 3 76 48.19% FB201231P00225000 2020-12-03 3:29PM EST 225.00 0.45 0.40 0.49 +0.03 *7.14% 2 164 45.90% FB201231P00230000 2020-12-03 2:22PM EST 230.00 0.52 0.50 0.60 0.03 -5.45% 3 249 43.82% FB201231P00235000 2020-12-03 2:30PM EST 235.00 0.69 0.65 0.77 +0.08 13.11% 12 285 42.14% FB201231P00240000 2020-12-03 3:29PM EST 240.00 0.89 0.85 0.97 +0.09-11.25% 78 307 40.27% FB201231P00245000 2020-12-03 3:57PM EST 245.00 1.21 1.14 1.27 +0.21 -21.00% 65 241 38.77% FB201231P00250000 2020-12-03 3:57PM EST 250.00 1.63 1.54 1.77 +0.20 +13.99% 205 472 37.99% FB201231P00252500 2020-12-03 2:25PM EST 252.50 1.85 1.78 2.06 0.21 +12 80% 47 201 37.50% FB201231P00255000 2020-12-03 3:49PM EST 255.00 2.33 2.08 2.39 +0.33 +16,50% 167 194 37.00% 2 Assume that the risk-free interest rate is 4.5% and the stock pays no dividends. Based on the information above- 1. Compute the implied volatilities for these calls and puts using different strike prices. Make separate Tables for calls and puts. 2. Use BSM formula to compute the price of calls and puts via Black-Scholes-Merton pricing formula using the implied volatilities in (1) above. 3. Find the difference between BSM price (using the implied volatility) and the actual option (market) price. 4. Explain your results in one paragraph. 5. Hints: Your table should look something like the following (Example of calls). Quote Date Expiry Date/Closin g date Option price (optio n Last) Strike price Current stock price at close Time to wunder Time in years de Interest rate CCR interest implied vol BSM price using implied vol Difference BSM-market 31/12/2020 9.83 282.50 281.85 31/12/2020 9.05 285.00 03/12/202 0 03/12/202 0 03/12/202 0 03/12/202 0 31/12/2020 8.35 287.50 31/12/2020 Notes: 1) Time to maturity is the number of days from quote day until expiry Excluding weekends) Note: time to maturity, -NETWORKDAYS(start_date, end_date, (holidays]) [use in excel file) 2) Time in years = time to maturity/252 3) Continuously compounded (CCR) interest rate = LN(int rate +1)







