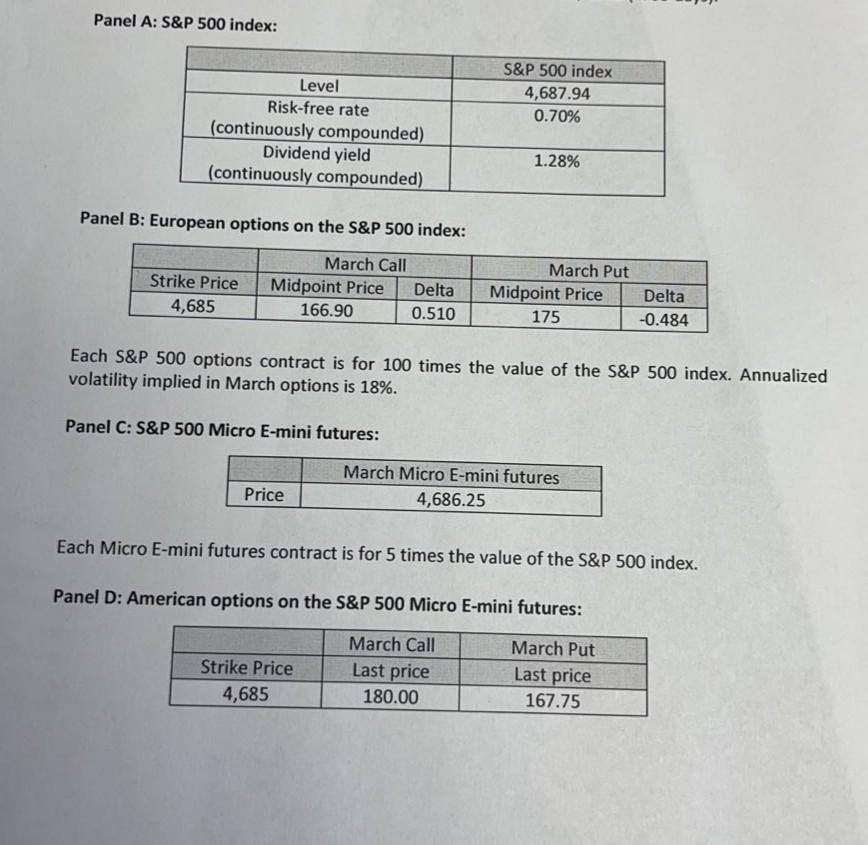
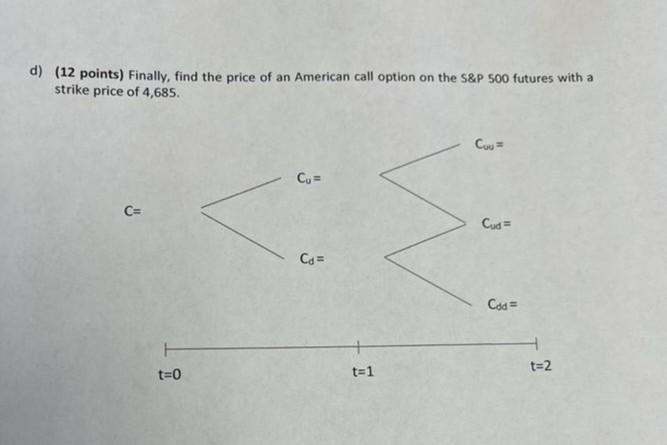
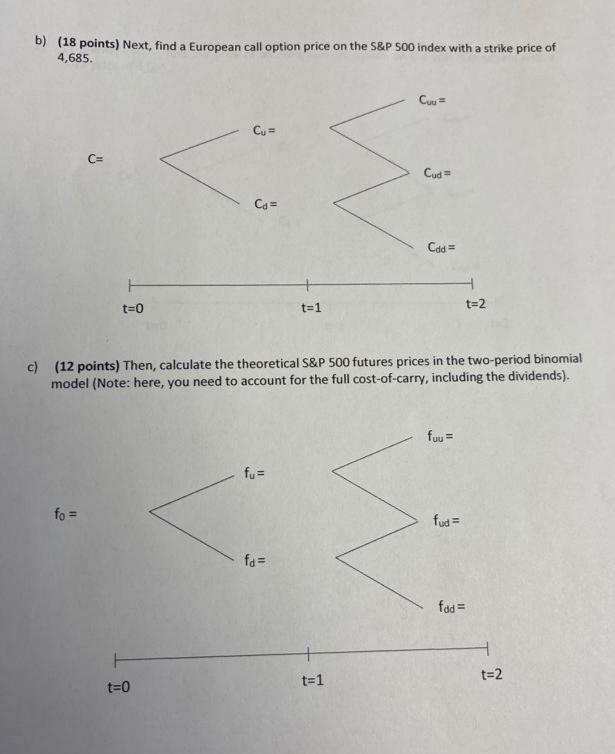
Please solve it in 30 minute please data for this queation is given in first page

Panel A: S&P 500 index: S&P 500 index 4,687.94 0.70% Level Risk-free rate (continuously compounded) Dividend yield (continuously compounded) 1.28% Panel B: European options on the S&P 500 index: Strike Price 4,685 March Call Midpoint Price Delta 166.90 0.510 March Put Midpoint Price 175 Delta -0.484 Each S&P 500 options contract is for 100 times the value of the S&P 500 index. Annualized volatility implied in March options is 18%. Panel C: S&P 500 Micro E-mini futures: Price March Micro E-mini futures 4,686.25 Each Micro E-mini futures contract is for 5 times the value of the S&P 500 index. Panel D: American options on the S&P 500 Micro E-mini futures: Strike Price 4,685 March Call Last price 180.00 March Put Last price 167.75 17. Pricing options on the S&P 500 Micro E-mini futures (54 points) Use a two-period binomial model to price March call options on the March S&P 500 futures. Suppose your research assistant atready calculated all the main parameters for the binomial model. These parameters already account for the fact that the index pays a continuously compounded dividend yield. Per-period risk-free rate = 0.095% Per-period up parameter = 1.071 Per-period down parameter = 0.934 Risk-neutral probability of an up movement = 0.489 Proceed in several steps. a) (12 points) First, determine the S&P 500 index values in the two-period binomial model. Because the up and down parameters are adjusted for the dividend yield, no additional adjustment for dividends is required when constructing the binomial tree for the S&P 500 index. Suu = Su = S =4,687.94 Sud = Sa= Sad t=0 t=1 t=2 d) (12 points) Finally, find the price of an American call option on the S&P 500 futures with a strike price of 4,685. Cou Cu = C= Cus= Ca= Cod = t=0 t=1 t=2 b) (18 points) Next, find a European call option price on the S&P 500 index with a strike price of 4,685. Cuu = Cu = C= Cuda Cs= Cdd = t=0 t=1 t=2 c) (12 points) Then, calculate the theoretical S&P 500 futures prices in the two-period binomial model (Note: here, you need to account for the full cost-of-carry, including the dividends). fuu = fu = fo = fud = fa= fod t=0 t=1 t=2 Panel A: S&P 500 index: S&P 500 index 4,687.94 0.70% Level Risk-free rate (continuously compounded) Dividend yield (continuously compounded) 1.28% Panel B: European options on the S&P 500 index: Strike Price 4,685 March Call Midpoint Price Delta 166.90 0.510 March Put Midpoint Price 175 Delta -0.484 Each S&P 500 options contract is for 100 times the value of the S&P 500 index. Annualized volatility implied in March options is 18%. Panel C: S&P 500 Micro E-mini futures: Price March Micro E-mini futures 4,686.25 Each Micro E-mini futures contract is for 5 times the value of the S&P 500 index. Panel D: American options on the S&P 500 Micro E-mini futures: Strike Price 4,685 March Call Last price 180.00 March Put Last price 167.75 17. Pricing options on the S&P 500 Micro E-mini futures (54 points) Use a two-period binomial model to price March call options on the March S&P 500 futures. Suppose your research assistant atready calculated all the main parameters for the binomial model. These parameters already account for the fact that the index pays a continuously compounded dividend yield. Per-period risk-free rate = 0.095% Per-period up parameter = 1.071 Per-period down parameter = 0.934 Risk-neutral probability of an up movement = 0.489 Proceed in several steps. a) (12 points) First, determine the S&P 500 index values in the two-period binomial model. Because the up and down parameters are adjusted for the dividend yield, no additional adjustment for dividends is required when constructing the binomial tree for the S&P 500 index. Suu = Su = S =4,687.94 Sud = Sa= Sad t=0 t=1 t=2 d) (12 points) Finally, find the price of an American call option on the S&P 500 futures with a strike price of 4,685. Cou Cu = C= Cus= Ca= Cod = t=0 t=1 t=2 b) (18 points) Next, find a European call option price on the S&P 500 index with a strike price of 4,685. Cuu = Cu = C= Cuda Cs= Cdd = t=0 t=1 t=2 c) (12 points) Then, calculate the theoretical S&P 500 futures prices in the two-period binomial model (Note: here, you need to account for the full cost-of-carry, including the dividends). fuu = fu = fo = fud = fa= fod t=0 t=1 t=2