Please solve the following problem. Thanks in advance for your help.
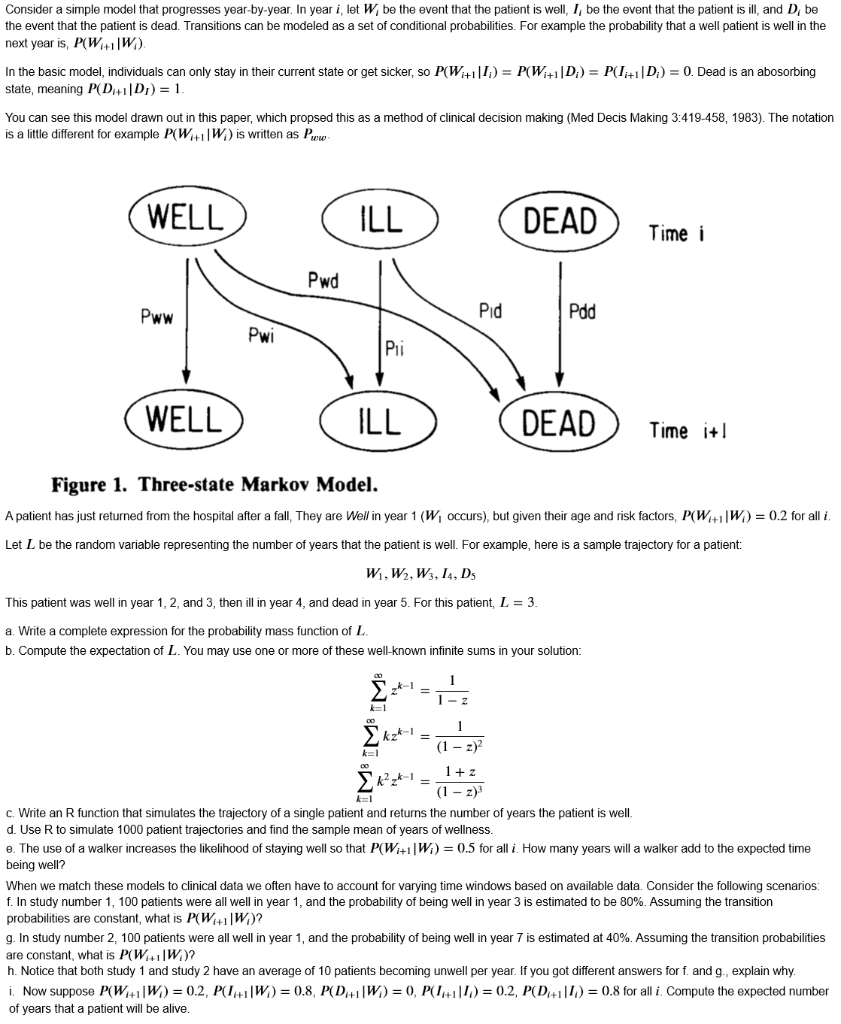
Consider a simple model that progresses year-by-year. In year i, let , be the event that the patient is well, /, be the event that the patient is ill, and D, be the event that the patient is dead. Transitions can be modeled as a set of conditional probabilities. For example the probability that a well patient is well in the next year is, P(W, [ WI). In the basic model, individuals can only stay in their current state or get sicker, so P(W |;) = P(Wit |D;) = P(I;+1 |D;) = 0. Dead is an abosorbing state, meaning P( DI [ Di) = 1. You can see this model drawn out in this paper, which propsed this as a method of clinical decision making (Med Decis Making 3:419-458, 1983). The notation is a little different for example P(W | W,) is written as Paw WELL ILL DEAD Time i Pwd Pww Pid Pdd Pw Pli WELL ILL DEAD Time itl Figure 1. Three-state Markov Model. A patient has just returned from the hospital after a fall, They are Well in year 1 (W/, occurs), but given their age and risk factors, P(W, [ W,) = 0.2 for all i. Let [ be the random variable representing the number of years that the patient is well. For example, here is a sample trajectory for a patient: WI, W2, W3, 14, Ds This patient was well in year 1, 2, and 3, then ill in year 4, and dead in year 5. For this patient, L = 3. a. Write a complete expression for the probability mass function of L. b. Compute the expectation of L. You may use one or more of these well-known infinite sums in your solution: 1 - kz*-1 K=1 (1 - z)2 IM 1+z (1 - z)3 c. Write an R function that simulates the trajectory of a single patient and returns the number of years the patient is well. d. Use R to simulate 1000 patient trajectories and find the sample mean of years of wellness. e. The use of a walker increases the likelihood of staying well so that P(With | W) = 0.5 for all i. How many years will a walker add to the expected time being well? When we match these models to clinical data we often have to account for varying time windows based on available data. Consider the following scenarios: f. In study number 1, 100 patients were all well in year 1, and the probability of being well in year 3 is estimated to be 80%. Assuming the transition probabilities are constant, what is P(W] [W,)? g. In study number 2, 100 patients were all well in year 1, and the probability of being well in year 7 is estimated at 40%. Assuming the transition probabilities are constant, what is P(W |WD)? h. Notice that both study 1 and study 2 have an average of 10 patients becoming unwell per year. If you got different answers for f. and g., explain why. Now suppose P(WHI [W,) = 0.2, P(I,1 [W,) = 0.8, P(D,+1 [W,) = 0, P(I,III,) = 0.2, P(D+1 |/,) = 0.8 for all i. Compute the expected number of years that a patient will be alive