Please solve the question with explaination
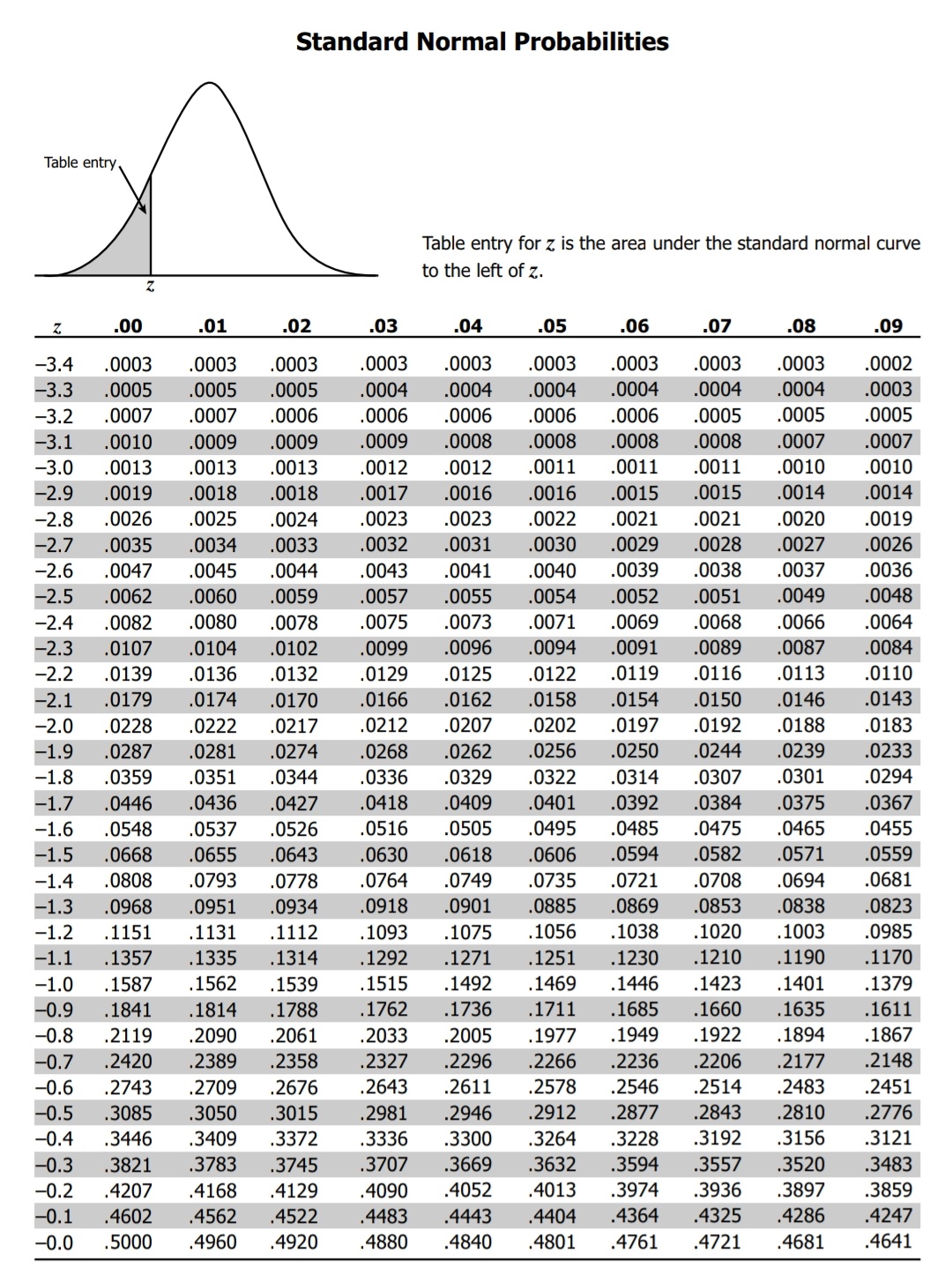
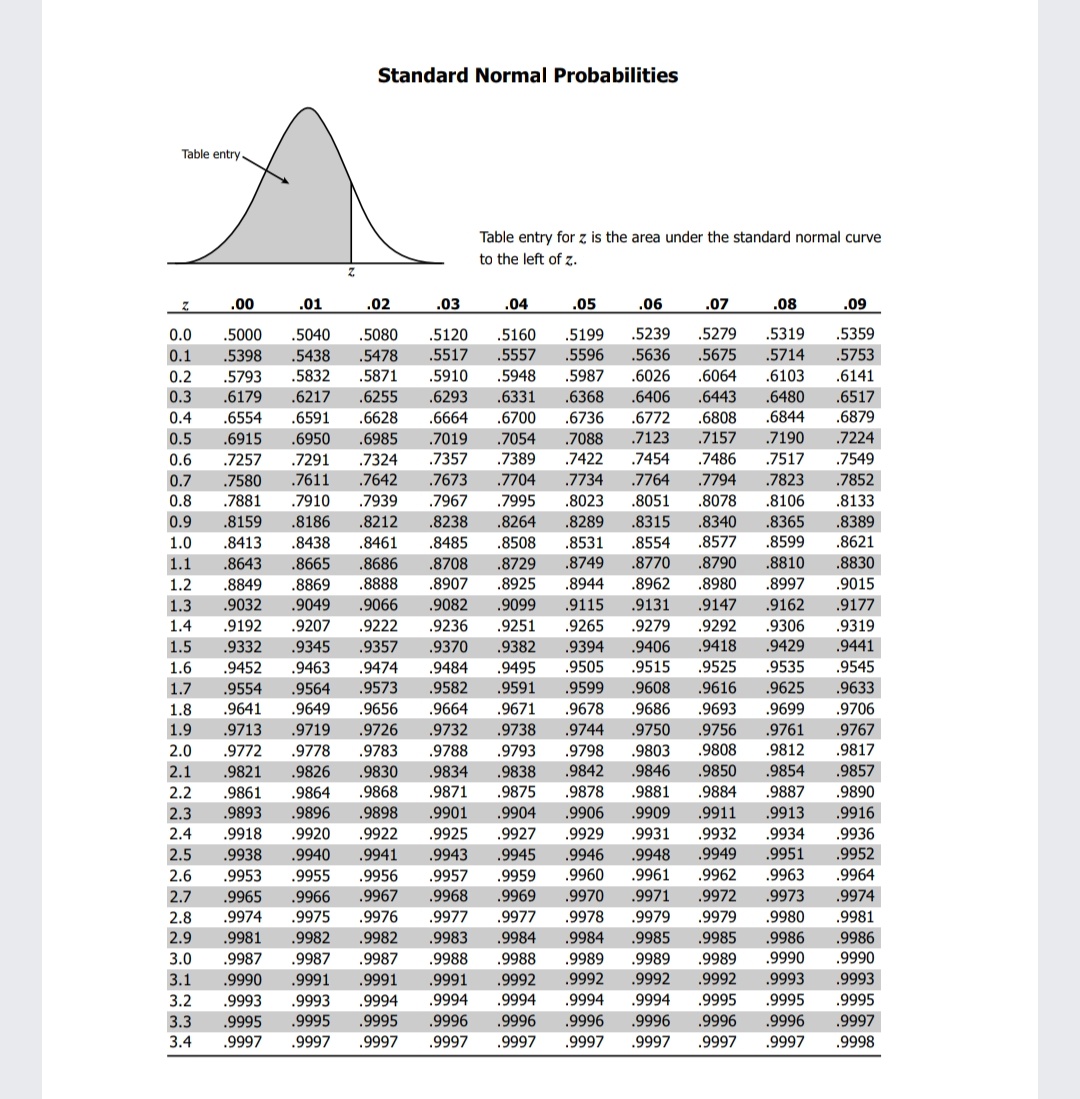
Standard Normal Probabilities Table entry for z is the area under the standard normal curve to the left of z. Z z .00 .01 .02 .03 .04 .05 .06 .07 .08 .09 3.4 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0003 .0002 3.2 .0007 .0007 .0006 .0006 .0006 .0006 .0006 .0005 .0005 .0005 3.0 .0013 .0013 .0013 .0012 .0012 .0011 .0011 .0011 .0010 .0010 2.8 .0026 .0025 .0024 .0023 .0023 .0022 .0021 .0021 .0020 .0019 2.6 .0047 .0045 .0044 .0043 .0041 .0040 .0039 .0038 .0037 .0036 2.4 .0082 .0080 .0078 .0075 .0073 .0071 .0069 .0068 .0066 .0064 2.2 .0139 .0136 .0132 .0129 .0125 .0122 .0119 .0116 .0113 .0110 2.0 .0228 .0222 .0217 .0212 .0207 .0202 .0197 .0192 .0188 .0183 1.8 .0359 .0351 .0344 .0336 .0329 .0322 .0314 .0307 .0301 .0294 1.6 .0548 .0537 .0526 .0516 .0505 .0495 .0485 .0475 .0465 .0455 1.4 .0808 .0793 .0778 .0764 .0749 .0735 .0721 .0708 .0694 .0681 1.2 .1151 .1131 .1112 .1093 .1075 .1056 .1038 .1020 .1003 .0985 1.0 .1587 .1562 .1539 .1515 .1492 .1469 .1446 .1423 .1401 .1379 0.8 .2119 .2090 .2061 .2033 .2005 .1977 .1949 .1922 .1894 .1867 0.6 .2743 .2709 .2676 .2643 .2611 .2578 .2546 .2514 .2483 .2451 -0.4 .3446 .3409 .3372 .3336 .3300 .3264 .3228 .3192 .3156 .3121 0.2 .4207 .4168 .4129 .4090 .4052 .4013 .3974 .3936 .3897 .3859 0.0 .5000 .4960 .4920 .4880 .4840 .4801 .4761 .4721 .4681 .4641 Standard Normal Probabilities Table entry Table entry for z is the area under the standard normal curve to the left of z. .00 .01 .02 .03 .04 .05 06 .07 .08 09 0.0 .5000 .5040 5080 5120 .5160 .5199 .5239 5279 .5319 .5359 0.1 .5398 5438 5478 .5517 .5557 .5596 .5636 .5675 .5714 .5753 0.2 5793 5832 5871 5910 5948 5987 .6026 .6064 .6103 .6141 0.3 6179 6217 6255 6293 6331 6368 .6406 6443 .6480 6517 0.4 6554 6591 6628 .6664 .6700 6736 6772 6808 6844 6879 0.5 6915 .6950 5985 7019 7054 7088 .7123 7157 .7190 .7224 0.6 .7257 7291 7324 .7357 .7389 .7422 .7454 .7486 .7517 .7549 0.7 .7580 .7611 7642 .7673 7704 .7734 .776 .7794 .7823 7852 0.8 .7881 .7910 .7939 7967 .7995 .8023 .8051 8078 .8106 .8133 0.9 8159 8186 .8212 .8238 8264 8289 .8315 .8340 .8365 .8389 1.0 .8413 8438 8461 8485 .8508 .8531 .8554 8577 .8599 .8621 1.1 8643 .8665 8686 .8708 8729 .8749 .8770 8790 .8810 8830 1.2 .8849 .8869 .8888 .8907 .8925 8944 .8962 .8980 .8997 .9015 1.3 9032 9049 9066 .9082 9099 .9115 .9131 9147 9162 9177 1.4 9192 9207 9222 9236 9251 9265 9279 9292 .9306 .9319 1.5 9332 9345 9357 9370 9382 .9394 .9406 9418 .9429 .9441 1.6 .9452 .9463 9474 .9484 .9495 .9505 .9515 .9525 9535 .9545 1.7 9554 9564 9573 9582 .9591 .9599 .9608 .9616 9625 .9633 1.8 .9641 9649 9656 9664 9671 9678 .9686 9693 .9699 9706 1.9 9713 .9719 9726 9732 9738 9744 9750 .9756 9761 9767 2.0 9772 9778 9783 9788 9793 9798 .9803 8086 .9812 9817 2.1 .9821 .9826 9830 9834 9838 .9842 .9846 .9850 .9854 .9857 2.2 9861 864 .9868 9871 .9875 .9878 .9881 .9884 .9887 .9890 2.3 .9893 9896 .9898 .9901 .9904 .9906 .9909 .9911 .9913 .9916 2.4 9918 9920 9922 9925 9927 9929 .9931 .9932 .9934 9936 2.5 .9938 9940 9941 9943 9945 9946 .9948 .9949 .9951 9952 2.6 .9953 9955 9956 9957 .9959 9960 .9961 9962 9963 .9964 2.7 9965 9966 .9967 .9968 .9969 .9970 .9971 .9972 .9973 9974 2.8 .9974 9975 9976 9977 .9977 9978 .9979 9979 .9980 9981 2.9 .9981 9982 9982 9983 .9984 .9984 .9985 .9985 .9986 9986 3.0 9987 9987 9987 9988 .9988 9989 .9989 .9989 9990 9990 3.1 .9990 9991 9991 9991 9992 9992 .9992 9992 .9993 .9993 3.2 .9993 9993 9994 9994 9994 9994 .9994 9995 .9995 .9995 3.3 9995 9995 9995 9996 9996 .9996 .9996 .9996 9996 .9997 3.4 .9997 9997 9997 .9997 .9997 .9997 .9997 .9997 .9997 .9998(b) The power W in a resistor is proportional to the voltage V. That is W=rV, where r is a constant. If r=2 and V can be assumed to be a normal random variable with mean 1.08 and standard deviation 1, find (i) Var(W) and (ii) Prob.(W)>0.8