

please solve these problems :
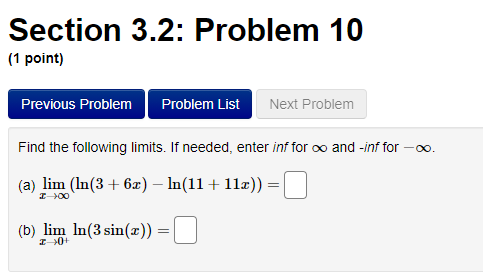
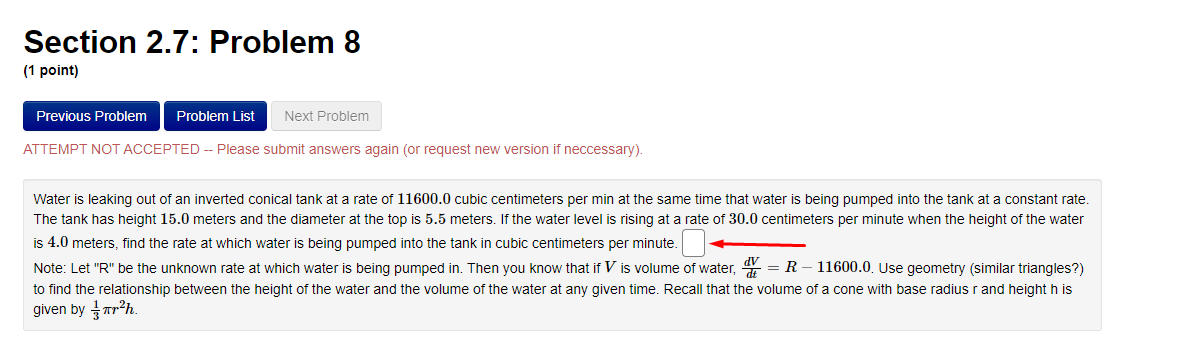
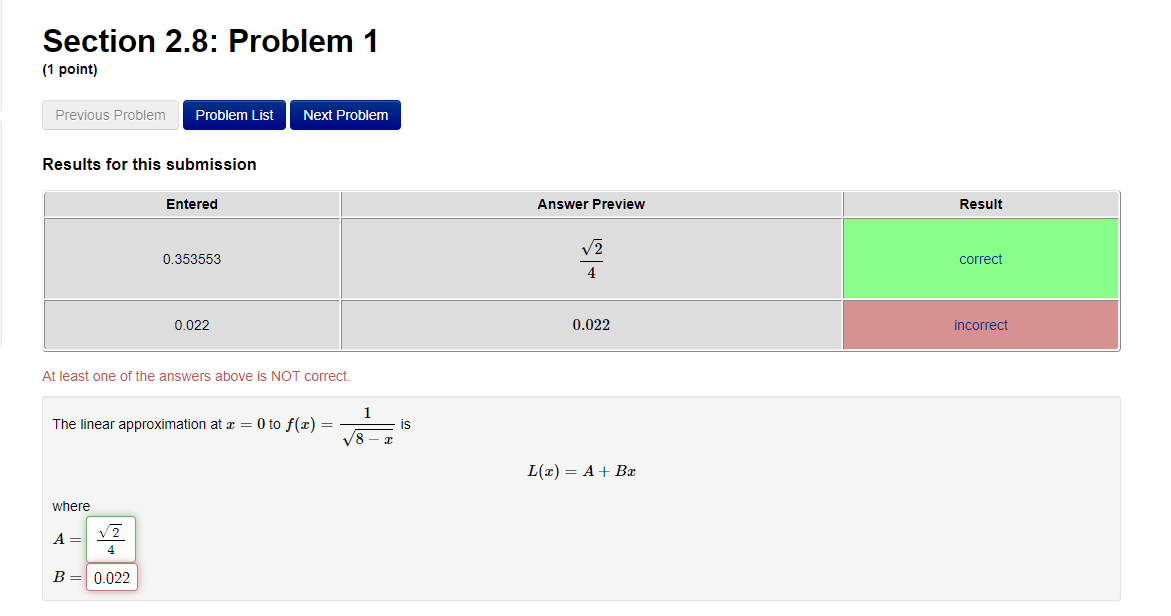
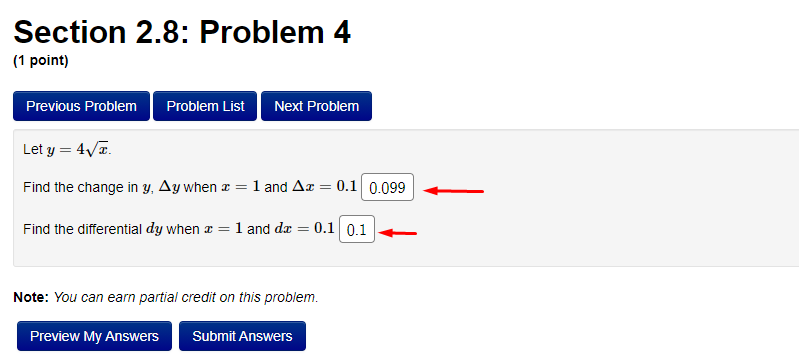
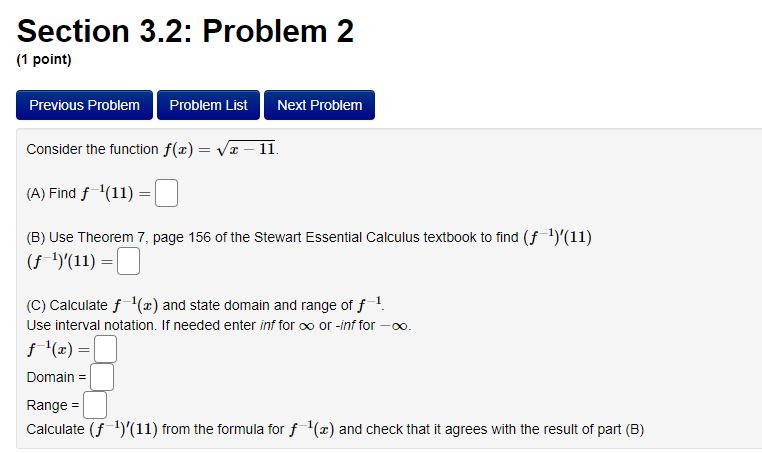
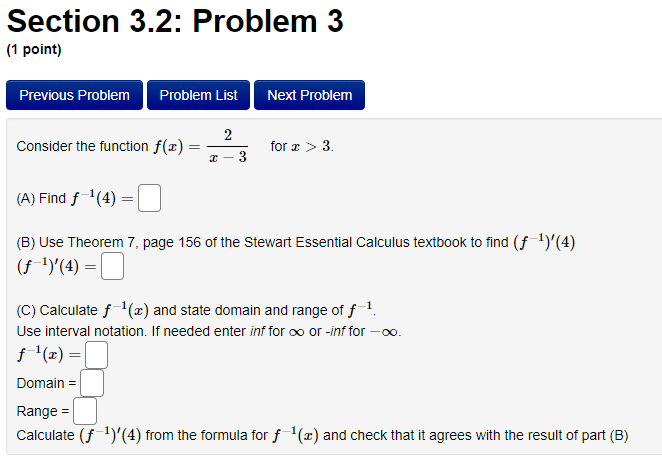
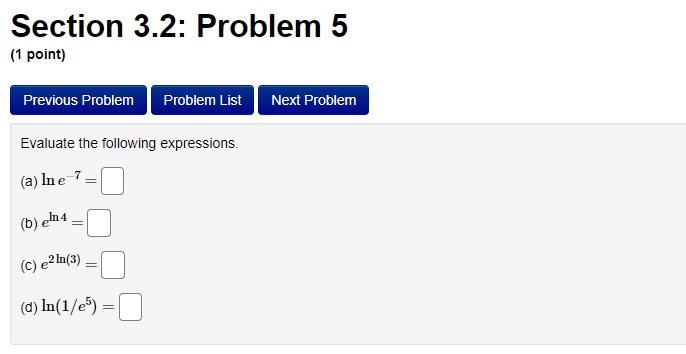
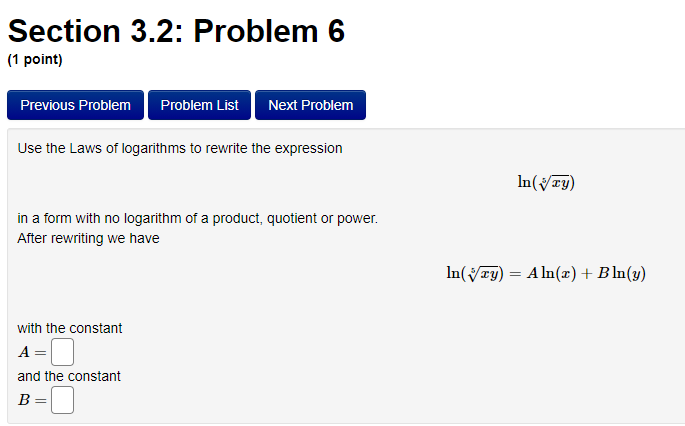
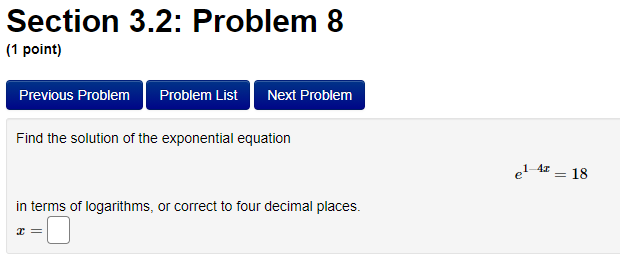
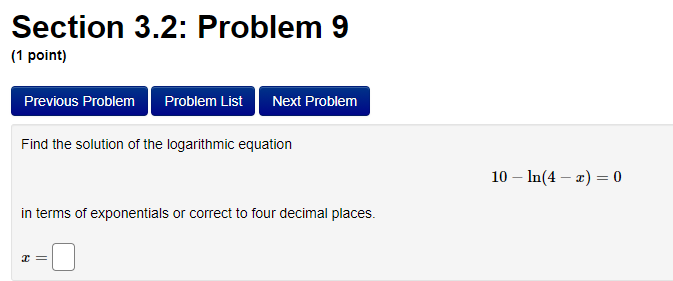
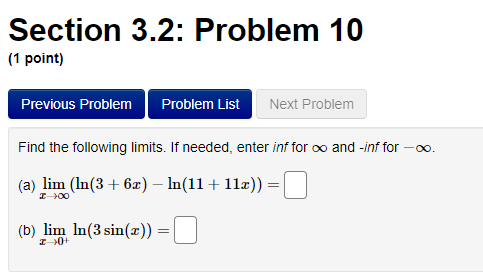
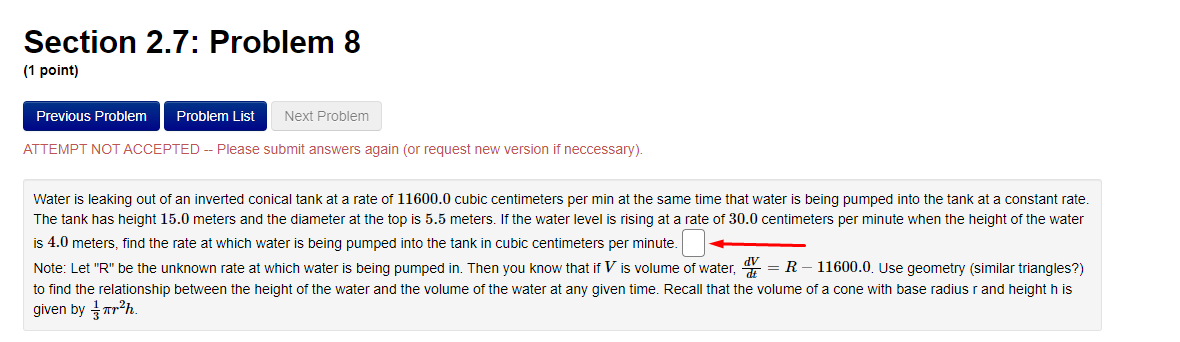
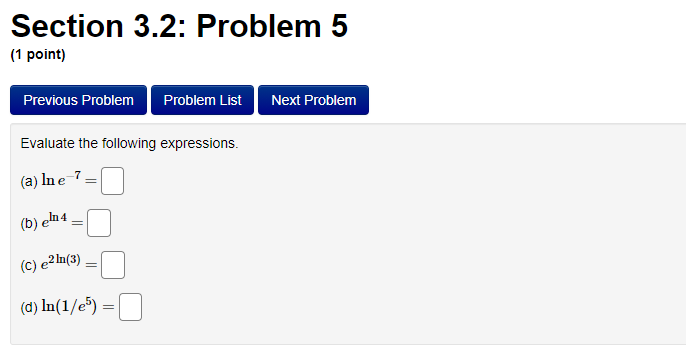
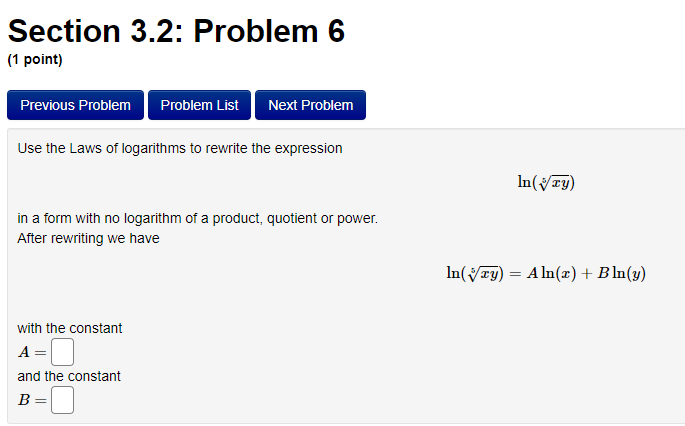
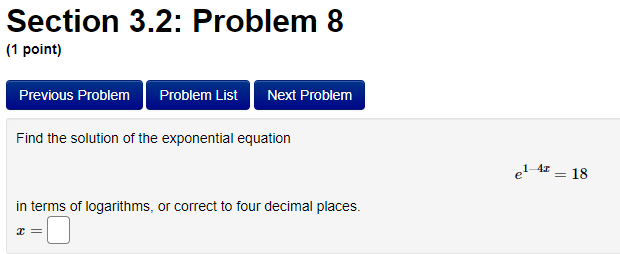
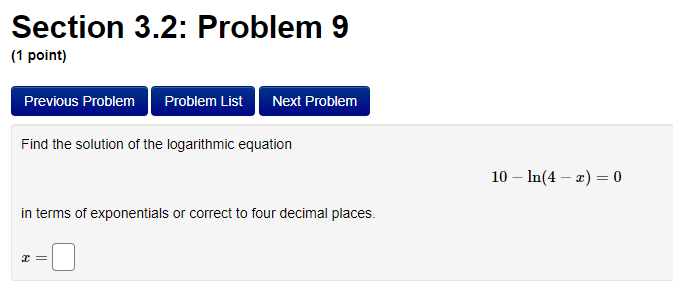
Section 3.2: Problem 1 (1 point) Previous Problem Problem List Next Problem Algebraically find the inverse function of f(x) = 2-5er. f 1(x) = Graph f, f and the line y = x on the same screen and check whether the graphs of f and fare reflections about the line.Section 3.2: Problem 10 (1 point) Previous Problem Problem List Next Problem Find the following limits. If needed, enter inf for co and -inf for -oo. (a) lim (In (3 + 6x) - I(11 + 113) ) = T-100 (b) lim In (3 sin (@) ) =Section 2.7: Problem 8 (1 point) Previous Problem Problem List Next Problem ATTEMPT NOT ACCEPTED -- Please submit answers again (or request new version if necessary). Water is leaking out of an inverted conical tank at a rate of 11600.0 cubic centimeters per min at the same time that water is being pumped into the tank at a constant rate. The tank has height 15.0 meters and the diameter at the top is 5.5 meters. If the water level is rising at a rate of 30.0 centimeters per minute when the height of the water is 4.0 meters, find the rate at which water is being pumped into the tank in cubic centimeters per minute. Note: Let "R" be the unknown rate at which water is being pumped in. Then you know that if V is volume of water, T, = R - 11600.0. Use geometry (similar triangles?) to find the relationship between the height of the water and the volume of the water at any given time. Recall that the volume of a cone with base radius r and height h is given by = mr h.Section 2.8: Problem 1 (1 point) Previous Problem Problem List Next Problem Results for this submission Entered Answer Preview Result 0.353553 V2 correct 0.022 0.022 incorrect At least one of the answers above is NOT correct. 1 The linear approximation at x = 0 to f(x) = is V8 - L(x) = A + Bx where A = V 2 4 B = 0.022Section 2.8: Problem 4 (1 point) Previous Problem Problem List Next Problem Let y = 4VE. Find the change in y, Ay when = = 1 and As = 0.1 0.099 Find the differential dy when x = 1 and de = 0.1 0.1 Note: You can earn partial credit on this problem. Preview My Answers Submit AnswersSection 3.2: Problem 2 (1 point) Previous Problem Problem List Next Problem Consider the function f(@) = vx - 11. (A) Find f (11) = (B) Use Theorem 7, page 156 of the Stewart Essential Calculus textbook to find (f )'(11) (f- 1)'(11) (C) Calculate f (x) and state domain and range of f Use interval notation. If needed enter inf for co or -inffor -o. f ' (x) = Domain = Range = Calculate (f ])'(11) from the formula for f () and check that it agrees with the result of part (B)Section 3.2: Problem 3 (1 point) Previous Problem Problem List Next Problem Consider the function f(* ) = for x > 3. c- 3 (A) Find f 1(4) = (B) Use Theorem 7, page 156 of the Stewart Essential Calculus textbook to find (f-!)'(4) (f 1 ) ' (4 ) = (C) Calculate f (x) and state domain and range of f . Use interval notation. If needed enter inf for co or -inffor -co. f (x) = Domain = Range = Calculate (f )'(4) from the formula for f (x) and check that it agrees with the result of part (B)Section 3.2: Problem 4 (1 point) Previous Problem Problem List Next Problem For each of the given functions f(), find the derivative (f ]) (c) at the given point c, first finding a = f (c). (See Theorem 7, page 156 of the Stewart Essential Calculus textbook) 1. f(x) = 3x + 623; c= -9 a = (f 1 )' ( c ) = 2. f(x) = x2 - 10x + 41 on the interval [5, co); c = 17 a = ( f 1 ) ' ( c ) =Section 3.2: Problem 5 (1 point) Previous Problem Problem List Next Problem Evaluate the following expressions. (a) Ine 7: (b) eln4 (c) e2 In(3) (d) In(1/e5) =Section 3.2: Problem 6 (1 point) Previous Problem Problem List Next Problem Use the Laws of logarithms to rewrite the expression In(cy) in a form with no logarithm of a product, quotient or power. After rewriting we have In(vry) = Aln(x) + BIn(y) with the constant A = and the constant BSection 3.2: Problem 7 [1 paint: PFEEWUUS Problem Problem List NEXT PIDDIEH'I Use the Laws of logan'thms to rewrite the expression in a form with no logarithm of a product, quotient or power. After rewnting we have with the constant A = C] the constant B = E] and the constant C = D Section 3.2: Problem 8 (1 point) Previous Problem Problem List Next Problem Find the solution of the exponential equation 18 in terms of logarithms, or correct to four decimal places. TSection 3.2: Problem 9 (1 point) Previous Problem Problem List Next Problem Find the solution of the logarithmic equation 10 - In(4 - x) = 0 in terms of exponentials or correct to four decimal places