Please Solve This Question

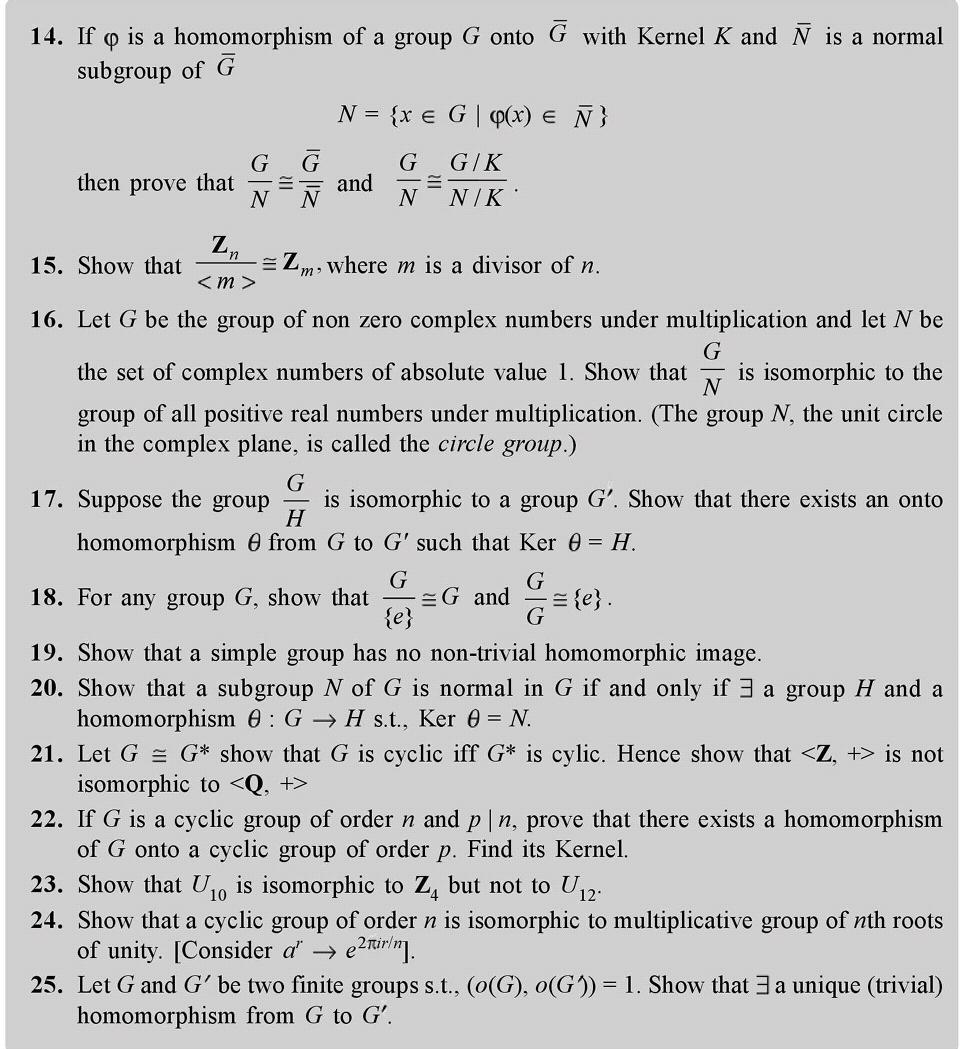
14. If q is a homomorphism of a group G onto G with Kernel K and N is a normal subgroup of G N = ( X E G| Q(X) E N) G G G GIK then prove that N N and N NIK . 15. Show that In = Zm, where m is a divisor of n. 16. Let G be the group of non zero complex numbers under multiplication and let N be the set of complex numbers of absolute value 1. Show that is isomorphic to the G group of all positive real numbers under multiplication. (The group N, the unit circle in the complex plane, is called the circle group.) 17. Suppose the group is isomorphic to a group G'. Show that there exists an onto homomorphism 0 from G to G' such that Ker 0 = H. 18. For any group G, show that =G and - =(e) {e} 19. Show that a simple group has no non-trivial homomorphic image. 20. Show that a subgroup N of G is normal in G if and only if 3 a group H and a homomorphism 0 : G - H s.t., Ker 0 = N. 21. Let G = G* show that G is cyclic iff G* is cylic. Hence show that is not isomorphic to 22. If G is a cyclic group of order n and p In, prove that there exists a homomorphism of G onto a cyclic group of order p. Find its Kernel. 23. Show that Uj is isomorphic to Z, but not to U12. 24. Show that a cyclic group of order n is isomorphic to multiplicative group of nth roots of unity. [Consider a" -> ezmirim]. 25. Let G and G' be two finite groups s.t., (o(G), o(G)) = 1. Show that 3 a unique (trivial) homomorphism from G to G