





Please solve this
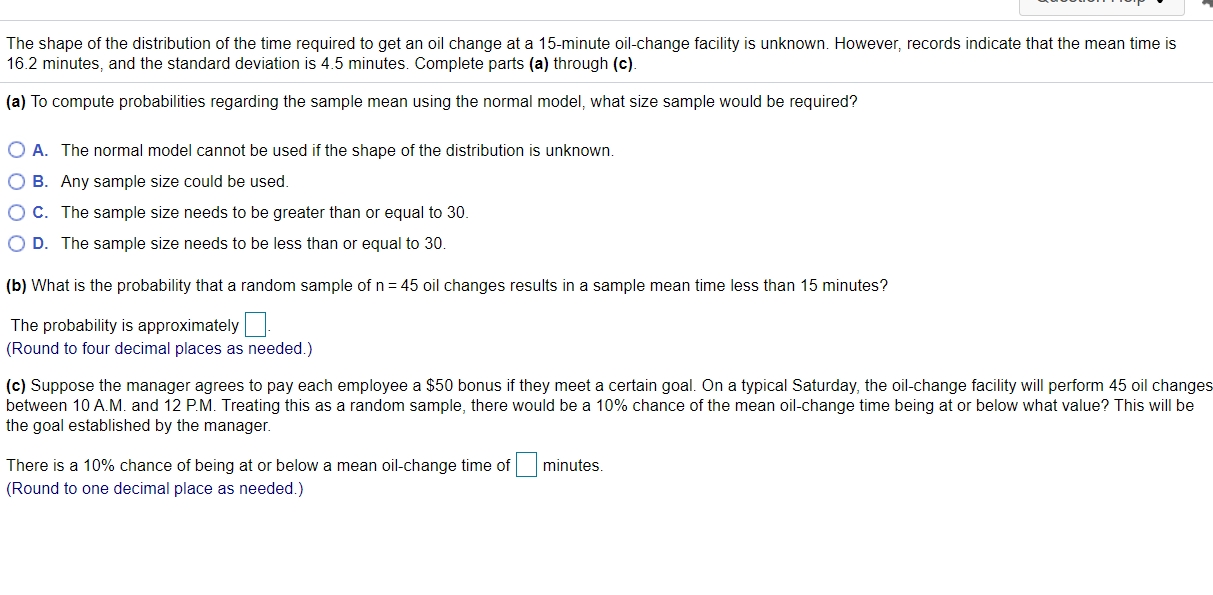
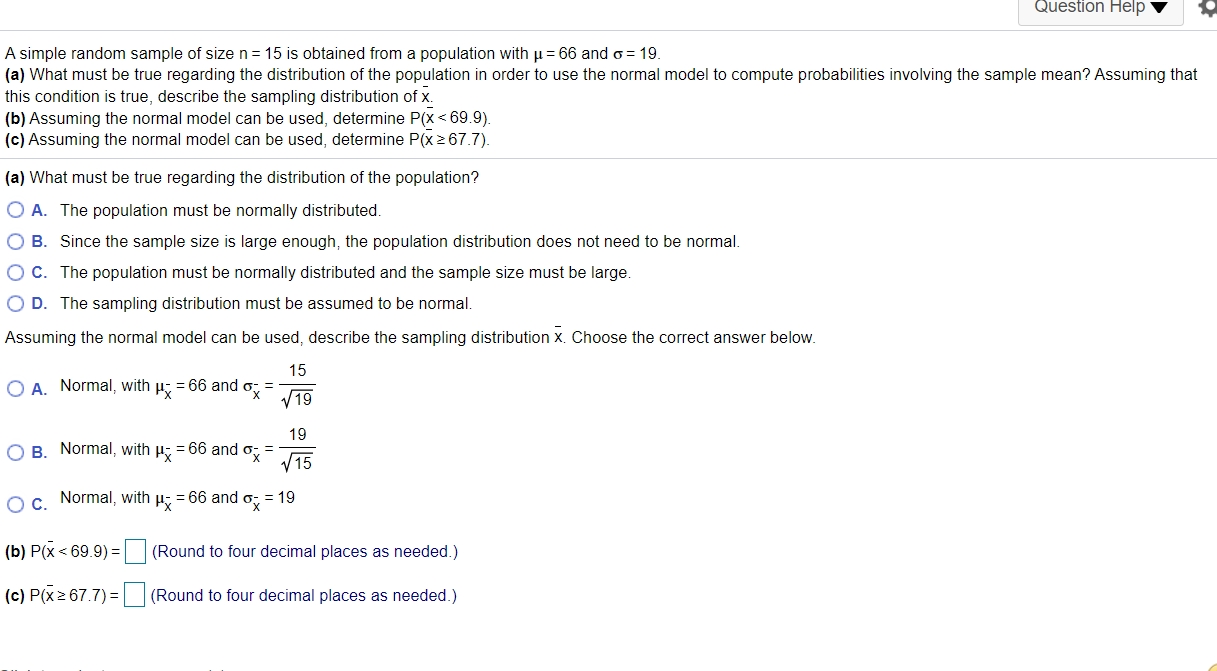
The shape of the distribution of the time required to get an oil change at a 15minute oilchange facility is unknown However, records indicate that the mean time is 16.2 minutes, and the standard deviation Is 4.5 minutes. Complete parts (a) through (c). (a) To compute probabilities regarding the sample mean using the normal model, what size sample would be required? 0 A. The normal model cannot be used if the shape of the distribution is unknown. 0 B. Any sample size could be used. 0 C. The sample size needs to be greater than or equal to 30. O D. The sample size needs to be less than or equal to 30. (b) What is the probability that a random sample of n : 45 oil changes results in a sample mean time less than 15 minutes? The probability is approximately . (Round to four decimal places as needed.) (c) Suppose the manager agrees to pay each employee a $50 bonus If they meet a certain goal. On a typical Saturday, the oilchange facility will perform 45 oil changes between 10 AM. and 12 PM. Treating this as a random sample, there would be a 10% chance of the mean oilchange time being at or below what value? This will be the goal established by the manager. There is a 10% chance of being at or below a mean oilchange time of minutes. (Round to one decimal place as needed.) \"1-\"-.. ""F i H The shape of the distribution of the time required to get an oil change at a 15minute oilchange facility is unknown. However, records indicate that the mean time is 16.2 minutes, and the standard deviation is 4.5 minutes. Complete parts (a) through (c). (a) To compute probabilities regarding the sample mean using the normal model, what size sample would be required? 0 A. The normal model cannot be used if the shape of the distribution is unknown. 0 B. Any sample size could be used. 0 C. The sample size needs to be greater than or equal to 30. O D. The sample size needs to be less than or equal to 30. (b) What is the probability that a random sample of n : 45 oil changes results in a sample mean time less than 15 minutes? The probability is apprommately . (Round to four decimal places as needed.) (1:) Suppose the manager agrees to pay each employee a $50 bonus if they meet a certain goal. On a typical Saturday, the oil-change facility will perform 45 oil changes between 10 AM. and 12 PM. Treating this as a random sample, there would be a 10% chance of the mean oilchange time being at or below what value? This will be the goal established by the manager. There is a 10% chance of being at or below a mean oilchange time of minutes. (Round to one decimal place as needed ) Question Help 7 Q A simple random sample of size n =15 is obtained from a population with p = 66 and 0 =19. (a) What must be true regarding the distribution of the population in orderto use the normal model to compute probabilities involving the sample mean? Assuming that this condition is true, describe the sampling distribution of x. (b) Assuming the normal model can be used, determine PQ_( 86.8) ? (c) What is P (x = 70.2) ? (d) What is P (74.4
86.8) = (Round to four decimal places as needed.) (c) P (x=70.2) = (Round to four decimal places as needed.) (d) P (74.4






















