PLEASE TAKE AS MUCH TIME AS YOU NEED TO SOLVE THIS PROBLEM, ALL I NEED IS A CORRECT ANSWER WITH ALL THE STEPS.

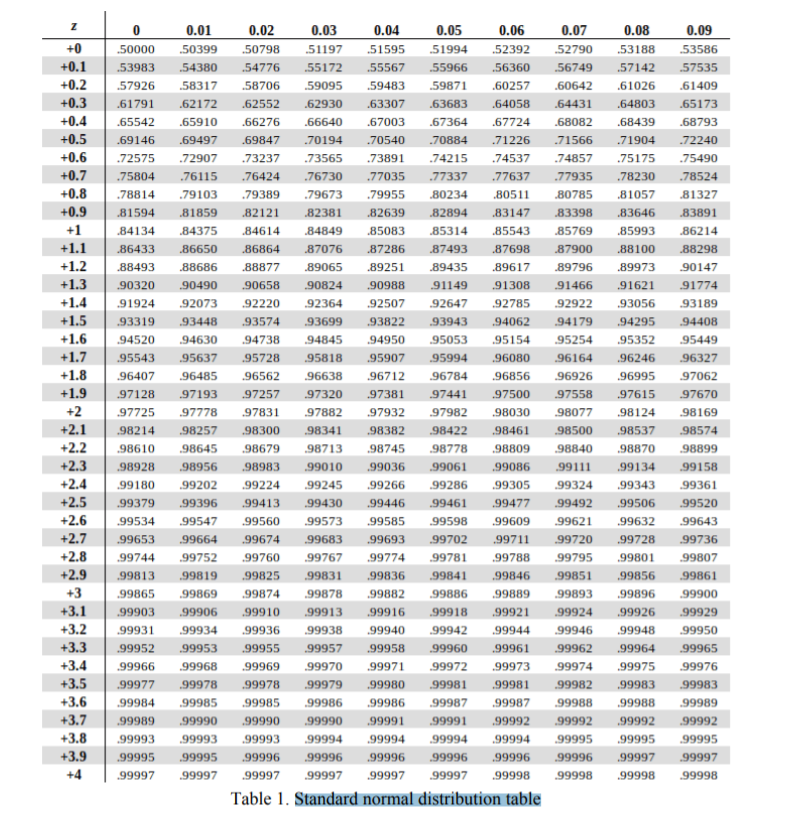
I WILL INCLUDE THE Standard normal distribution table JUST IN CASE YOU NEED IT.

THANK YOU!!

part (1) A reporter from Ron Appetite magazine bought 8 bagels from Fairmount bagels. Each bagel was weighed and yielded the following data (grants): 109.5, 111.6, 117.6, 109.2, 110.8, 119.1, 115.2, 112.5 a) Assuming that the eight bagels were randomly sampled and that the weight of a bagel is normally distributed, estimate the true average weight and standard deviation of the weight using maximum likelihood estimation. Please show the procedure for deriving the expressions of the estimates, and then plug in the weights for the numerical results. b) Again assuming a normal distribution, estimate the weight below which 95% of all bagels will have their weights. [Hint what is the 95'll percentile in temrs of ,u and 0?] Parttz) Suppose we want to do a poll to see what is the percentage. p of voters that will support president candidate A over candidate B. Assume that whether a person will vote for candidate A over candidate B is a Bernoulli trial, and the chance of a person voting for either candidate is equal. a) How many people do you need to poll so that the percentage p is within 1% from its true value with 95% condence? [Hint: The percentage p is the mean of the random variables which represent a vote for candidate A over candidate B] b) If you poll 400 people, how many have to prefer candidate A to B so that the 90% condence interval is entirely above p=0.5'? 0.09 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 .53188 .53586 +0 50000 50399 50798 51197 51595 51994 52392 52790 57535 +0.1 53983 54380 54776 55172 55567 55966 56360 56749 .57142 58317 .58706 .59095 .59483 59871 .60257 .60642 .61026 61409 +0.2 57926 .62552 62930 .63307 63683 64058 64431 64803 65173 +0.3 61791 62172 +0.4 65542 .65910 66276 66640 67003 67364 67724 .68082 .68439 .68793 .71904 .72240 +0.5 69146 69497 69847 .70194 .70540 .70884 71226 71566 .73565 .73891 .74215 74537 74857 .75175 .75490 +0.6 72575 72907 73237 +0.7 75804 76115 .76424 .76730 77035 77337 77637 77935 .78230 .78524 .81327 +0.8 78814 .79103 79389 .79673 .79955 80234 80511 80785 .81057 81859 .82121 .82381 .82639 82894 83147 .83398 .83646 .83891 +0.9 81594 .85543 .85769 85993 .86214 +1 .84134 84375 .84614 84849 85083 .85314 .86864 87076 87286 87493 87698 87900 .88100 .88298 +1.1 86433 86650 90147 +1.2 88493 88686 .88877 .89065 89251 89435 89617 89796 89973 +1.3 90320 90490 90658 90824 90988 91149 91308 91466 91621 91774 92220 92364 92507 92647 92785 92922 93056 93189 +1.4 91924 92073 +1.5 93319 93448 93574 93699 93822 93943 94062 94179 94295 .94408 +1.6 94520 94630 94738 94845 .94950 95053 .95154 95254 95352 95449 +1.7 95543 95637 95728 95818 .95907 95994 96080 96164 96246 96327 +1.8 96407 96485 96562 96638 .96712 .96784 96856 96926 96995 97062 +1.9 97128 97193 97257 97320 97381 97441 97500 97558 97615 97670 +2 97725 97778 97831 97882 97932 97982 98030 98077 .98124 98169 98257 98300 98341 98382 98422 98461 98500 .98537 98574 +2.1 98214 98809 .98840 98870 98899 +2.2 98610 .98645 98679 98713 98745 98778 99134 .99158 +2.3 98928 .98956 98983 99010 99036 .99061 99086 99111 99324 99343 .99361 +2.4 99180 99202 .99224 99245 99266 .99286 99305 +2.5 .99379 99396 .99413 99430 .99446 99461 99477 99492 99506 99520 +2.6 99534 99547 99560 99573 .99585 99598 99609 99621 99632 99643 +2.7 99653 99664 99674 99683 .99693 99702 99711 99720 .99728 99736 99760 .99767 99774 99781 99788 99795 99801 99807 +2.8 99744 99752 +2.9 99813 99819 99825 99831 99836 99841 99846 99851 .99856 99861 99896 99900 +3 99865 99869 99874 99878 99882 99886 99889 99893 99929 +3.1 99903 99906 99910 99913 99916 99918 99921 99924 99926 99946 99948 99950 +3.2 99931 99934 99936 99938 99940 99942 99944 99962 .99964 99965 +3.3 99952 99953 99955 99957 .99958 99960 99961 99975 99976 +3.4 99966 .99968 .99969 99970 .99971 99972 99973 99974 +3.5 99977 99978 99978 99979 .99980 99981 99981 99982 .99983 99983 99986 .99986 99987 99987 99988 .99988 99989 +3.6 99984 .99985 .99985 .99990 .99990 .99990 99991 99991 99992 99992 .99992 99992 +3.7 99989 +3.8 99993 .99993 99993 99994 99994 99994 99994 .99995 99995 99995 +3.9 99995 99995 99996 99996 99996 99996 99996 99996 99997 .99997 .99998 +4 99997 99997 99997 99997 .99997 99997 .99998 99998 .99998 Table 1. Standard normal distribution table