Please this within 1 hour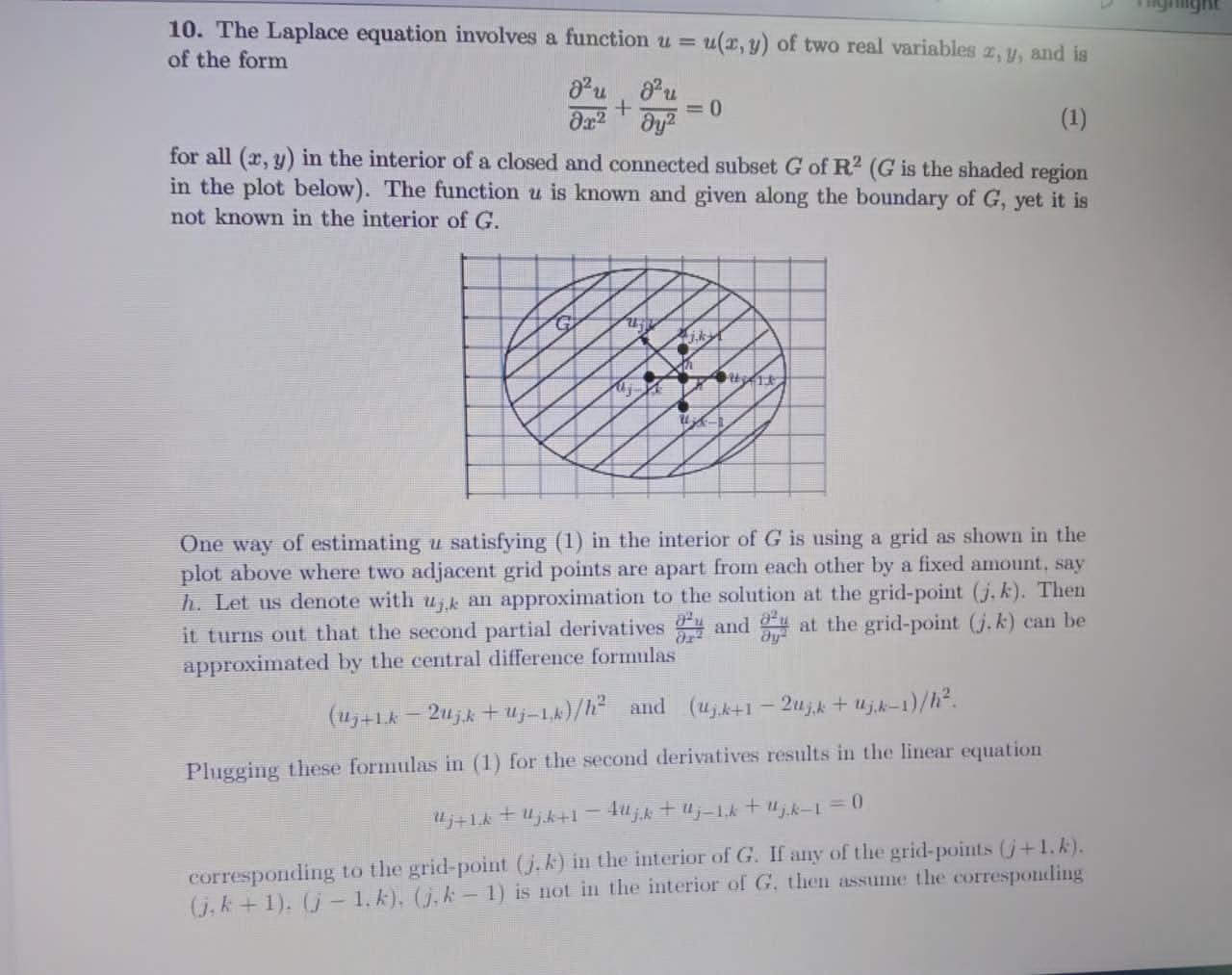

+ 10. The Laplace equation involves a function u = u(x, y) of two real variables 2, y, and is of the form au du = 0 x2 * y2 (1) for all (2, y) in the interior of a closed and connected subset G of R? (G is the shaded region in the plot below). The function u is known and given along the boundary of G, yet it is not known in the interior of G. uit . U- One way of estimating u satisfying (1) in the interior of G is using a grid as shown in the plot above where two adjacent grid points are apart from each other by a fixed amount, say h. Let us denote with ujk an approximation to the solution at the grid-point (j.k). Then it turns out that the second partial derivatives and at the grid-point (.k) can be approximated by the central difference formulas (13+16 - 2uj.k + uz-1,6)/1? and (ujk+1 24.3k + uj.k-1)/ Plugging these formulas in (1) for the second derivatives results in the linear equation U;+ 12 + Ujht1 - 4ught Uj-bh tu; k-1 = 0 corresponding to the grid-point (.k) in the interior of G. If any of the grid-points (i+1.k). 6.k+1). (j - 1. k). (,k - 1) is not in the interior of G. then assume the corresponding Uy+1,4, Uz,k+1, uj-14, 14;.*-1 is given by the value of u at the nearest point on the boundary of G, and hence known. This results in a system of linear equations in the variables ujk for the grid-points in the interior of G. The number of linear equations is as many as the number of variables, as there is one equation for every variable ujk. Show that this system of linear equations has a unique solution (Hint: First consider the system of homogeneous linear equations, which occurs when u is equal to zero along the boundary of G. Show such a homogeneous system has a unique solution, then try to generalize.) + 10. The Laplace equation involves a function u = u(x, y) of two real variables 2, y, and is of the form au du = 0 x2 * y2 (1) for all (2, y) in the interior of a closed and connected subset G of R? (G is the shaded region in the plot below). The function u is known and given along the boundary of G, yet it is not known in the interior of G. uit . U- One way of estimating u satisfying (1) in the interior of G is using a grid as shown in the plot above where two adjacent grid points are apart from each other by a fixed amount, say h. Let us denote with ujk an approximation to the solution at the grid-point (j.k). Then it turns out that the second partial derivatives and at the grid-point (.k) can be approximated by the central difference formulas (13+16 - 2uj.k + uz-1,6)/1? and (ujk+1 24.3k + uj.k-1)/ Plugging these formulas in (1) for the second derivatives results in the linear equation U;+ 12 + Ujht1 - 4ught Uj-bh tu; k-1 = 0 corresponding to the grid-point (.k) in the interior of G. If any of the grid-points (i+1.k). 6.k+1). (j - 1. k). (,k - 1) is not in the interior of G. then assume the corresponding Uy+1,4, Uz,k+1, uj-14, 14;.*-1 is given by the value of u at the nearest point on the boundary of G, and hence known. This results in a system of linear equations in the variables ujk for the grid-points in the interior of G. The number of linear equations is as many as the number of variables, as there is one equation for every variable ujk. Show that this system of linear equations has a unique solution (Hint: First consider the system of homogeneous linear equations, which occurs when u is equal to zero along the boundary of G. Show such a homogeneous system has a unique solution, then try to generalize.)