PLEASE TRY TO SOLVE IT, ANY HELP IS APPRECIATED

PLEASE TRY TO EXPLAIN THE CODE

I WILL DEFINATELY UPVOTE

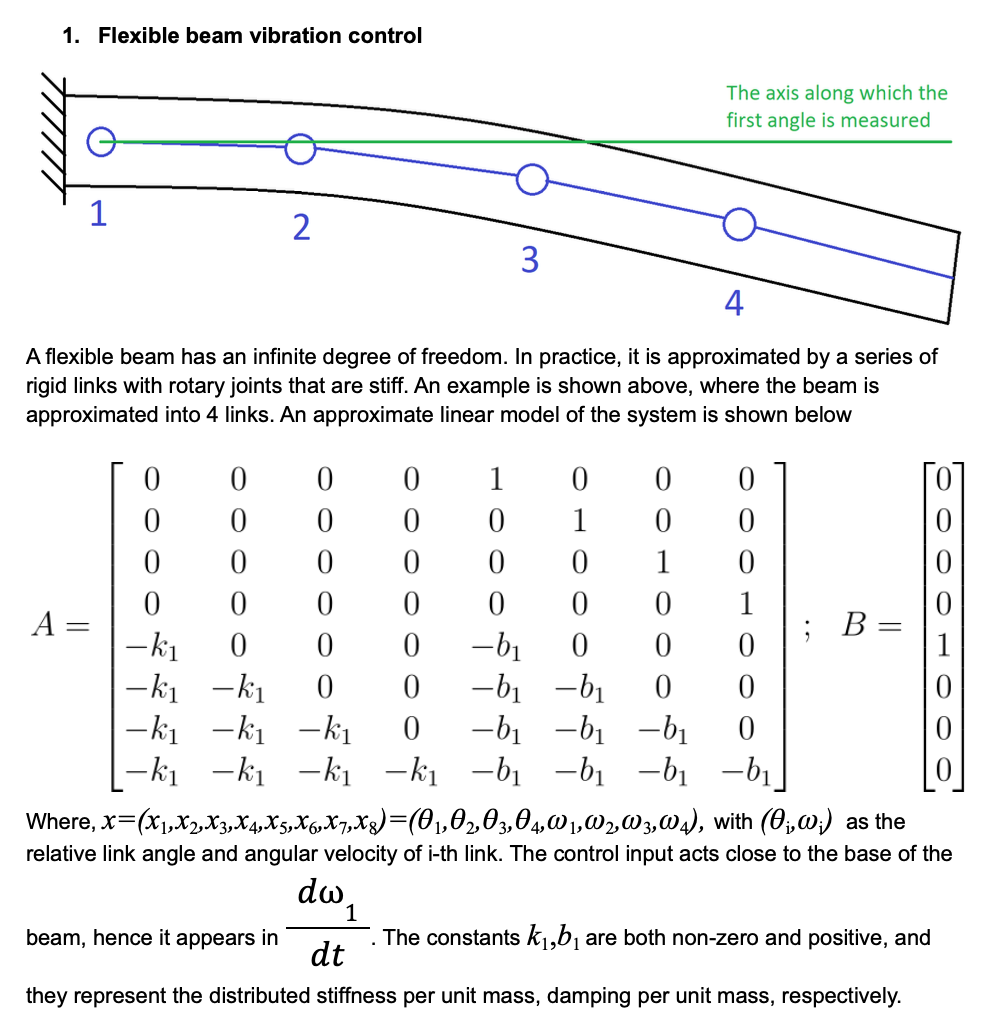
1. Flexible beam vibration control The axis along which the first angle is measured 1 2 3 4. A flexible beam has an infinite degree of freedom. In practice, it is approximated by a series of rigid links with rotary joints that are stiff. An example is shown above, where the beam is approximated into 4 links. An approximate linear model of the system is shown below 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 A= B = - ki 0 0 0 -bi 0 0 0 -ki -ki 0 0 -by - b 0 0 0 -ki -ki -ki 0 -bi-b1 -b1 0 0 -ki -ki -ki -ki-bi-b1 -bi -61 Where, x=(x1,x2,X3,X4,X5,X6,X7,xx)=(01,02,03,04,01,02,03,04), with (0;,0;) as the relative link angle and angular velocity of i-th link. The control input acts close to the base of the dw 1 beam, hence it appears in The constants k,b, are both non-zero and positive, and dt they represent the distributed stiffness per unit mass, damping per unit mass, respectively. . C. (4 marks) Take kq=1, b,=0.0001. Assume full state information is available. Simulate a pole placement controller, choose poles such that all the vibrations get arrested within 1 sec, level of vibrations is within magnitude 0.01 for every state after 1 sec (use trial and error to get the poles). Use these initial conditions (please attach code which generates the plots): i. x(0)=(0.1,0.1,0.1,0.1,0,0,0,0) ii. x(0)=(0.1,-0.1,0.1,-0.1,0,0,0,0) iii. x(O)=(0.1,0.1,0.1,0.1,1,1,1,1) iv. x(0)=(0.1,-0.1,0.1,-0.1,1,-1,1,-1) d. (2 marks) A single strain gauge has to be fitted on the beam at one of the assumed joint vicinities. This means that there will be only one output. The strain gauge will give the angular deviation in that vicinity. Where should the strain gauge be placed such that we will be able to estimate all other states using the single output? 1. Flexible beam vibration control The axis along which the first angle is measured 1 2 3 4. A flexible beam has an infinite degree of freedom. In practice, it is approximated by a series of rigid links with rotary joints that are stiff. An example is shown above, where the beam is approximated into 4 links. An approximate linear model of the system is shown below 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 A= B = - ki 0 0 0 -bi 0 0 0 -ki -ki 0 0 -by - b 0 0 0 -ki -ki -ki 0 -bi-b1 -b1 0 0 -ki -ki -ki -ki-bi-b1 -bi -61 Where, x=(x1,x2,X3,X4,X5,X6,X7,xx)=(01,02,03,04,01,02,03,04), with (0;,0;) as the relative link angle and angular velocity of i-th link. The control input acts close to the base of the dw 1 beam, hence it appears in The constants k,b, are both non-zero and positive, and dt they represent the distributed stiffness per unit mass, damping per unit mass, respectively. . C. (4 marks) Take kq=1, b,=0.0001. Assume full state information is available. Simulate a pole placement controller, choose poles such that all the vibrations get arrested within 1 sec, level of vibrations is within magnitude 0.01 for every state after 1 sec (use trial and error to get the poles). Use these initial conditions (please attach code which generates the plots): i. x(0)=(0.1,0.1,0.1,0.1,0,0,0,0) ii. x(0)=(0.1,-0.1,0.1,-0.1,0,0,0,0) iii. x(O)=(0.1,0.1,0.1,0.1,1,1,1,1) iv. x(0)=(0.1,-0.1,0.1,-0.1,1,-1,1,-1) d. (2 marks) A single strain gauge has to be fitted on the beam at one of the assumed joint vicinities. This means that there will be only one output. The strain gauge will give the angular deviation in that vicinity. Where should the strain gauge be placed such that we will be able to estimate all other states using the single output