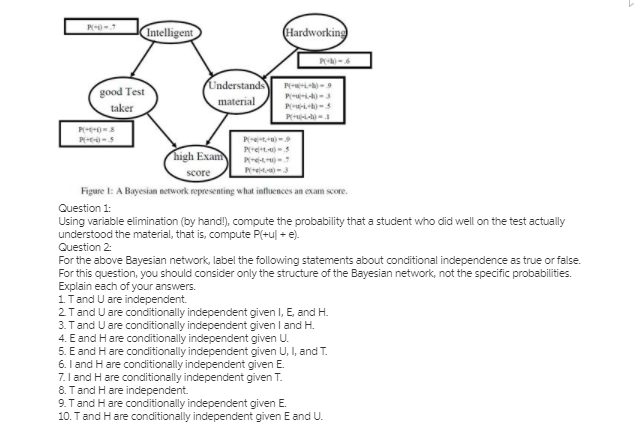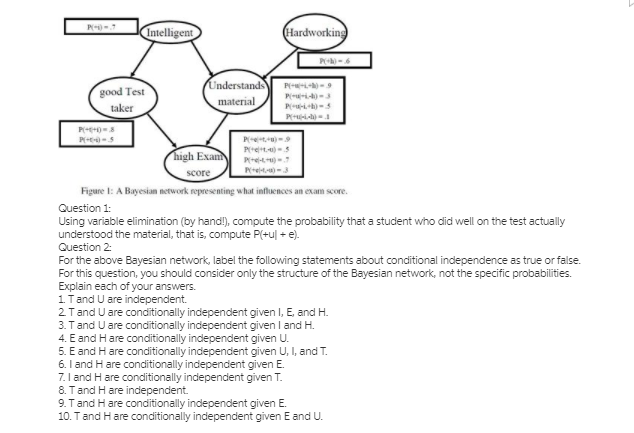
please tutor solve using hand written and don't copy peoples work
\fProblem 1 [Conditional probability| Two courses, ECE 280 and ECE 980, each have sophomores, juniors, and seniors enrolled, as shown in the following table. ECE 280 ECEDED Total sophomore junior 05 70 Total 100 250 Random variable * = s, is used to model the class outcome of an experiment with 3, = 1, X = =2, and X = Is indicating outcomes sophomore, junior, and senior, respectively. A probability experiment consists of selecting a course, then selecting a student from the chosen course. The participants in the study are more curious about ECE 960 and select that course SUX of the time Let By = the event "home ECE 20 and B, "- the event "douse ECE 290", so that P( 8,) = 0.2 and P(B,) = 0.B Determine the following quantities for the experiment: . P(z.(B,) and P(r. (8.) for i - 1.2.3. . Fx(s| B.) bureR. . /x(x(B,) force R. . P(X = x,) for i = 1,2,3. Problem 2 [Poisson distribution] The number of data packets arriving in I see at a particular switch (in millions) is modeled by railo variable X which is Poisson distributed with parameter A = 2. (a) Find the probability that X = 3 million packets arrive in a given second. (b) Find the probability that X = 0 packets arrive.You work for a consulting engineering firm who has been contracted by the Australian Border Force to evaluate two commercial solutions which are being considered for the next generation border control system. This system utilises iris recognition to verify individuals as they enter the country through international airports. The system employs verification only: a person presents their passport; the system then checks to see if the identity of the person matches the identity of the person named on the passport. This match is conducted by comparing an iris image of the person taken at the border, with the iris image stored on their e-passport. In the border control system, the verification test has two outcomes: 1. V+: the person is verified (i.e., their iris image taken at the border matches that stored on their e-passport); or 2. V-: the person is not verified. In reality, the person could be: 1. P+: a genuine traveller, who has their own unique and valid passport; or 2. P-: an imposter, who is not genuine and has a fake or stolen passport (for example). Each commercial solution has strengths and weaknesses. The specifications released by the commercial providers are given in the table below. It is also known from historical data that the probability of a person being an imposter is 0.12%. Commercial Solution Solution 1 - Eyematch Solution 2 - Bullseye The system correctly verifies a genuine traveller. 98.26% 98.35% The system incorrectly verifies an imposter. 5.12% 5.18%% 1) Calculate Conditional Probabilities Your firm is to compute the conditional probability (for both solutions) that there Is an Imposter, given the verification Is positive; ie. p(P-[V+). Show all your calculations using Bayes' rule. 2) Provide a Recommendation Provide your recommendations to the Australian Border Force on the best cholce of the solution If they want to minimise this conditional probablyIty. This question relates to dealing with uncertainty.Exercise 4 Suppose that a current industry-standard engineering model predicts that a certain type of concrete block will have a 40% chance of failure when subject to a two-tonne load. A civil engineer wants to test the accuracy of this claim by obtaining 50 independent samples of such blocks, subjecting each to a two-tonne load and then recording the total number X of blocks that broke. She decides that she will reject the claim Ho : p = 04 in favour of Ha :p 0.4 if X