Please use Jupyter notebook to answer the question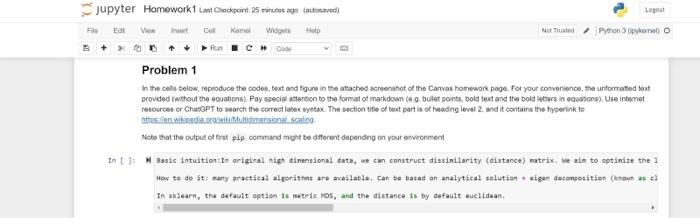

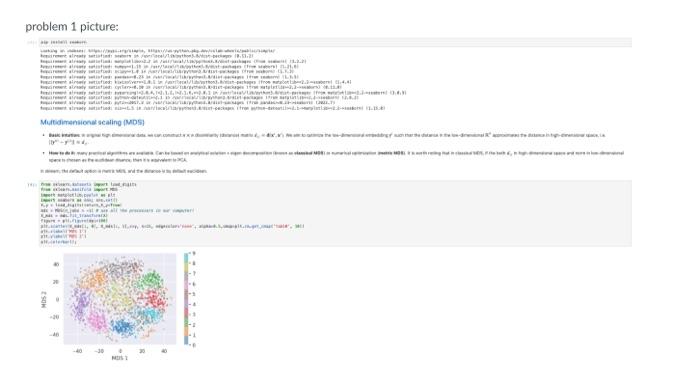
In the cels below, repeoduce the codes, bext and figure in tse atiached screenshot of the Convas homework poge. For your convenionce, the urtomated toxt provided (without the ecuebions). Pay esecial attention to the format of markdown (e. 0 . bulet ponts, bold teat and the boil listers in eqasions). Use intemet resources or CharGPT to seareh the correct latex syetax. The section tife of text part is of heding level 2 . and it eontains the toperink to Note that the cutput of frat pip cormand might be dfferent deponding on your otvirorment M Jasic intuition'In opiginal nigh dinensional dats, we can construct dissinilarity (distance) natrix. We alm to optinite the I Mow to do it: many aractical algorithat aro availablo, Can be baced an analytical selution t digan decongesition (keopun as el In skiearn, tha default eptien is metric. Mos, and the distance is by default euclidean, wit betlow teation Muftidimanional sealing [MDS] att ateinetili zoomed in text: Multidimensional scaling (MDS) - Basic intuition: In original high dimensional data, we can construct nn dissimilarity (distance) matrix dij=d(xi,xj). We aim to optimize the low-dimensional embedding y such that the distance in the low-dimensional Rk approximates the distance in highdimensional space, i.e. y(i)y(j)dij. - How to do it: many practical algorithms are available. Can be based on analytical solution + eigen decomposition (known as classical MDS) or numerical optimization (metric MDS). It is worth noting that in classical MDS, if the both dij in high-dimensional space and norm in low-dimensional space is chosen as the euclidean disance, then it is equivalent to PCA. In sklearn, the default option is metric MDS, and the distance is by default euclidean. Repeat the procedures of the in-class exercise in lecture 1 for matrix multiplication instead of inner-product. It is fine if your defined function only works for two squared matrix, and N here denotes the number of rows.columns. Compare the running time of your defined function with the correct matrix multiplication function (search by yourself) in Numpy. All other requirements are the same with in-class exercise