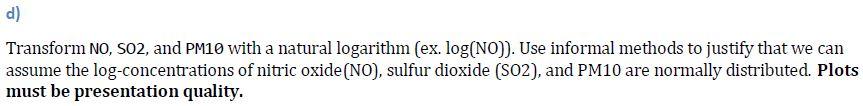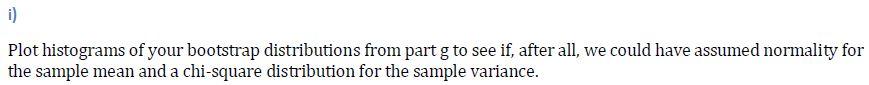Please, use R. The set data can be downloaded after installing the package "texmex". Please, provide solution details and the R code. Thank you.



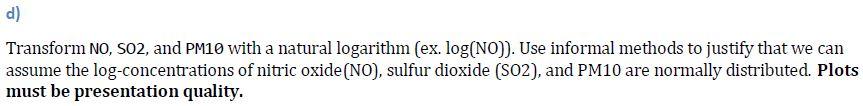



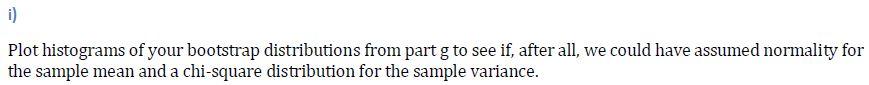
Install the R package texmex and load the data set winter. If you have trouble with this, a.csv file containing the winter data can be found on Carmen. This data set contains measurements on air pollution data from the Leeds, United Kingdom city center, collected from 1994 to 1998, including: 03 (ozone), NO2 (nitrogen dioxide), NO (nitric oxide), s02 (sulfur dioxide), and PM10 (coarse particulate matter, 10 micrometers in diameter or smaller). The winter data set corresponds to the months of November to February inclusive. Some outliers have been removed, as discussed by Heffernan and Tawn, 2004. b) Examine the concentration of nitrogen dioxide. Plot a histogram to justify that nitrogen dioxide concentration is reasonably normally distributed. Plots must be presentation quality. For instance, "winter$N02" is not an acceptable label c) Compute a 99% two-sided confidence interval for uno,, the mean concentration for nitrogen dioxide between November and February, inclusive. Include units and interpret your interval in the context of this problem. Use your interval to test Ho: Mnoz = 44 vs. Ho: no, 7 44 at significance level 0.01. d) Transform NO, SO2, and PM10 with a natural logarithm (ex. log(NO)). Use informal methods to justify that we can assume the log-concentrations of nitric oxide (NO), sulfur dioxide (SO2), and PM10 are normally distributed. Plots must be presentation quality. e) Daily air quality levels are categorized as good, fair, poor, and hazardous. A log-SO2 concentration less than 2.8 log- parts per billion is acceptable for "good" air quality. Test Ho: Mlog (902) = 2.8 vs. Ho: Mlog (502) 110 ppba at significance level 0.01. Do the following without the function VarTest: sketch the sampling distribution of the test statistic, compute the test statistic, compute the rejection region, compute the confidence interval, and test the hypothesis. Then check your answers with VarTest. Comment on what your answer means in the context of asthmatic individuals. h) Plot ozone concentration and log-concentration with presentation quality plots. Because these data appear quite non-normal, compute 99% confidence intervals for Mo, and 002, the mean and standard deviation of ozone concentration, using bootstrapping. Include your code. Include units and interpret your intervals in the context of this problem. i) Plot histograms of your bootstrap distributions from partg to see if, after all, we could have assumed normality for the sample mean and a chi-square distribution for the sample variance. Install the R package texmex and load the data set winter. If you have trouble with this, a.csv file containing the winter data can be found on Carmen. This data set contains measurements on air pollution data from the Leeds, United Kingdom city center, collected from 1994 to 1998, including: 03 (ozone), NO2 (nitrogen dioxide), NO (nitric oxide), s02 (sulfur dioxide), and PM10 (coarse particulate matter, 10 micrometers in diameter or smaller). The winter data set corresponds to the months of November to February inclusive. Some outliers have been removed, as discussed by Heffernan and Tawn, 2004. b) Examine the concentration of nitrogen dioxide. Plot a histogram to justify that nitrogen dioxide concentration is reasonably normally distributed. Plots must be presentation quality. For instance, "winter$N02" is not an acceptable label c) Compute a 99% two-sided confidence interval for uno,, the mean concentration for nitrogen dioxide between November and February, inclusive. Include units and interpret your interval in the context of this problem. Use your interval to test Ho: Mnoz = 44 vs. Ho: no, 7 44 at significance level 0.01. d) Transform NO, SO2, and PM10 with a natural logarithm (ex. log(NO)). Use informal methods to justify that we can assume the log-concentrations of nitric oxide (NO), sulfur dioxide (SO2), and PM10 are normally distributed. Plots must be presentation quality. e) Daily air quality levels are categorized as good, fair, poor, and hazardous. A log-SO2 concentration less than 2.8 log- parts per billion is acceptable for "good" air quality. Test Ho: Mlog (902) = 2.8 vs. Ho: Mlog (502) 110 ppba at significance level 0.01. Do the following without the function VarTest: sketch the sampling distribution of the test statistic, compute the test statistic, compute the rejection region, compute the confidence interval, and test the hypothesis. Then check your answers with VarTest. Comment on what your answer means in the context of asthmatic individuals. h) Plot ozone concentration and log-concentration with presentation quality plots. Because these data appear quite non-normal, compute 99% confidence intervals for Mo, and 002, the mean and standard deviation of ozone concentration, using bootstrapping. Include your code. Include units and interpret your intervals in the context of this problem. i) Plot histograms of your bootstrap distributions from partg to see if, after all, we could have assumed normality for the sample mean and a chi-square distribution for the sample variance