Please write a code for all of #8 in Matlab. Thanks!

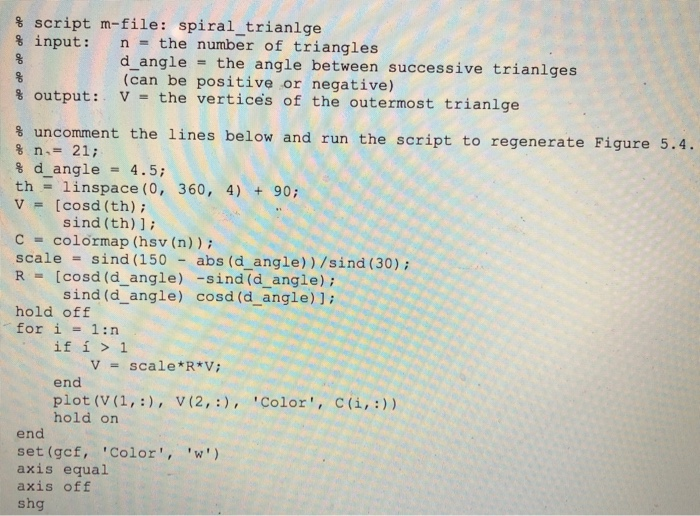
8) The figure to the right, and the thick red triangle in particular, shows 30 how the scaling factor was calculated in spiral triangle. The vari- able s in the figure is the length of the longest side of the red triangle, scale in the code, where 1 is the length of the vertical side. And a is the bottom angle of the red triangle, which is d angie in the code.o a) Modify spiral triangle to spiral, square so that it generates spi- rals using a square rather than an equilateral triangle. Successive squares must touch just as the triangles do. b) Then generalize this script file to spiralgon.n so that it generates spirals using a regular polygon with m sides for any m 2 3. Successive polygons must touch just as the triangles do. -1 0 1 Figure 5.5 % script m-file: spiral-trianlge % input: n- the number of triangles d angle -the angle between successive trianlges (can be positive or negative) % output: V- the vertices of the outermost triange he lines below and run the script to regenerate Figure 5.4 % n.- 21; % dangle-4.5; th=linspace ( 0, 360, 4) + 90; V[cosd (th) sind (th); c colormap (hsv (n)) scale = sind (150 - abs (d-angle)) /sind (30); R [cosd (d_angle) -sind(d_angle) ; sind (d_angle) cosd (d angle)]; hold off for i -1:n V scale*A*V; end plot (V (1,), v (2,), 'Color', c(i, :)) hold on end set (gcf, 'Color', 'w') axis equal axis off shg 8) The figure to the right, and the thick red triangle in particular, shows 30 how the scaling factor was calculated in spiral triangle. The vari- able s in the figure is the length of the longest side of the red triangle, scale in the code, where 1 is the length of the vertical side. And a is the bottom angle of the red triangle, which is d angie in the code.o a) Modify spiral triangle to spiral, square so that it generates spi- rals using a square rather than an equilateral triangle. Successive squares must touch just as the triangles do. b) Then generalize this script file to spiralgon.n so that it generates spirals using a regular polygon with m sides for any m 2 3. Successive polygons must touch just as the triangles do. -1 0 1 Figure 5.5 % script m-file: spiral-trianlge % input: n- the number of triangles d angle -the angle between successive trianlges (can be positive or negative) % output: V- the vertices of the outermost triange he lines below and run the script to regenerate Figure 5.4 % n.- 21; % dangle-4.5; th=linspace ( 0, 360, 4) + 90; V[cosd (th) sind (th); c colormap (hsv (n)) scale = sind (150 - abs (d-angle)) /sind (30); R [cosd (d_angle) -sind(d_angle) ; sind (d_angle) cosd (d angle)]; hold off for i -1:n V scale*A*V; end plot (V (1,), v (2,), 'Color', c(i, :)) hold on end set (gcf, 'Color', 'w') axis equal axis off shg