Please write everything out for each part!
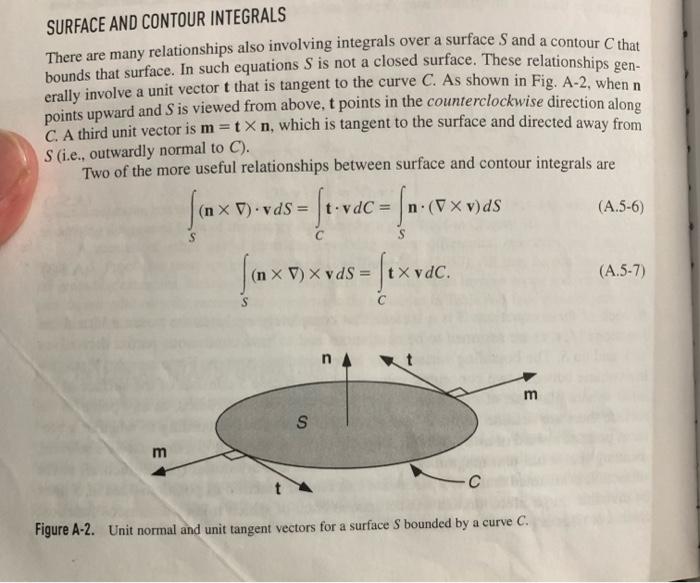
2-7. Species Accumulation and Transport within an Interface Accumulation and transport within an interface can be important for species that reside at phase boundaries, such as gases adsorbed on solids or surfactants at fluid-fluid interfaces. The objective is to derive more general interfacial conservation statements than those in Section 2.2. Consider a species that may be present at an interface or in either of the adjacent bulk phases. Let CS and NS be its surface concentration (moles m2 ) and surface flux (molesm1s1 ), respectively; note the differences in units from the corresponding three-dimensional quantities. The vector NS is everywhere tangent to the surface. (a) For part of an interface corresponding to surface S in Fig. A-2, state the macroscopic (integral) solute conservation equation. Assume that phase A is below S and phase B above it, such that n points toward the latter. Include the possibility of chemical reactions at the interface, transport to or from the bulk phases, and interfacial motion. The interface is not necessarily planar. (b) By reducing the integral equation of part (a) to a partial differential equation, show that tCS=SNS+[(NCvI)A(NCvI)B]n+RS where N and C are the species flux and concentration, respectively, in a bulk phase. (Subscripts identifying the chemical species have been dropped for simplicity.) This result, which is valid instantaneously and locally, is equivalent to Eq. (5.2-2) of Edwards et al. (1991). How does it compare with what is obtained by applying Eq. (2.215) to a chemical species? A result applicable to any point on the interface is obtained by letting SI be an arbitrarily small surface containing that point. Arguments like those used to derive Eq. (2.2-12) lead to a pointwise interfacial balance that is valid at any instant, namely, [(Fbv1)B(Fbv1)A]n1=BS. With F being the flux relative to fixed coordinates, Fbv1 is the flux relative to the interface. Thus, Eq. (2.2-15) shows that an interfacial source creates a difference in the normal components of the fluxes relative to the interface. In general, all of the quantities involved are functions of position, so that the balance changes from point to point on the interface. that V and S depend on time and vS=0. In such cases an additional term must be added to Eq. (2.2-1) to account for the fact that surface motion per se creates a flux relative to the surface. The term nvSdS represents the rate of volume gain caused by the motion of an element of the control surface, and the product of this and the local concentration gives the corresponding rate of entry of a given quantity into the control volume. Thus, the conservation equation for a moving control volume is dtdV(t)bdV=S(t)nFdS+V(t)BVdV+S(t)bnvSdS where the effects of surface motion are included now in the last term. This can be put in a more compact form using the Leibniz formula for differentiating a volume integral (Section A.5), dtdbdV=tbdV+bnvSdS There are many relationships also involving integrals over a surface S and a contour C that bounds that surface. In such equations S is not a closed surface. These relationships generally involve a unit vector t that is tangent to the curve C. As shown in Fig. A-2, when n points upward and S is viewed from above, t points in the counterclockwise direction along C. A third unit vector is m=tn, which is tangent to the surface and directed away from S (i.e., outwardly normal to C ). Two of the more useful relationships between surface and contour integrals are S(n)vdS=CtvdC=Sn(v)dSS(n)vdS=CtvdC Figure A-2. Unit normal and unit tangent vectors for a surface S bounded by a curve C. .L PRUPERIIES UF LINEAR BUUNUAKY-VALUL PRUBLEMS LINEARITY A differential equation that involves a single dependent variable, (r,t) (e.g., temperature), will be linear only if two requirements are met: (1) it contains no products of -dependent terms and (2) is not the argument of another function. That is, neither nor its derivatives can be multiplied by functions of , and terms such as exp() are not allowed. In a set of equations governing multiple dependent variables, a hallmark of a nonlinear system is the presence of any product of those variables. These requirements for linearity apply both to ordinary differential equations and to partial differential equations. Certain general relationships are best expressed using operator notation. Let L be a differential operator that contains one or more spatial derivatives and perhaps also a time derivative. A partial differential equation based on such an operator is represented generally as L=S(r) where S(r) is a given function of position. If S=0, the differential equation is homogeneous; if S=0, it is nonhomogeneous. If the operator is linear, it will satisfy L(a11+a22)=a1L1+a22 [(FbvI)B(FbvI)A]nI=BS