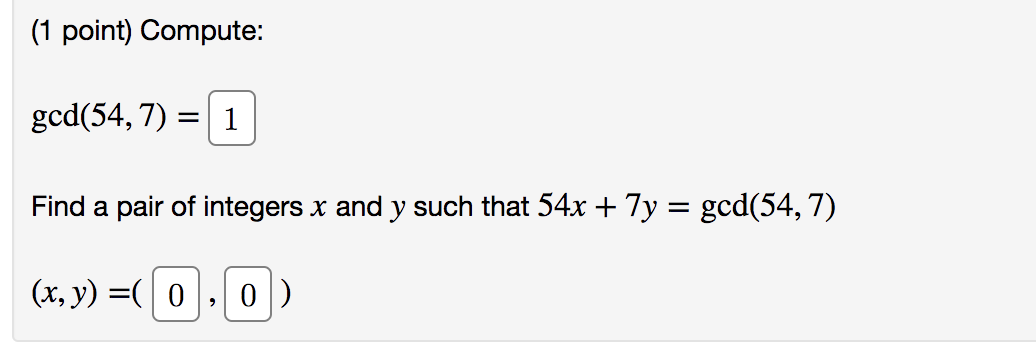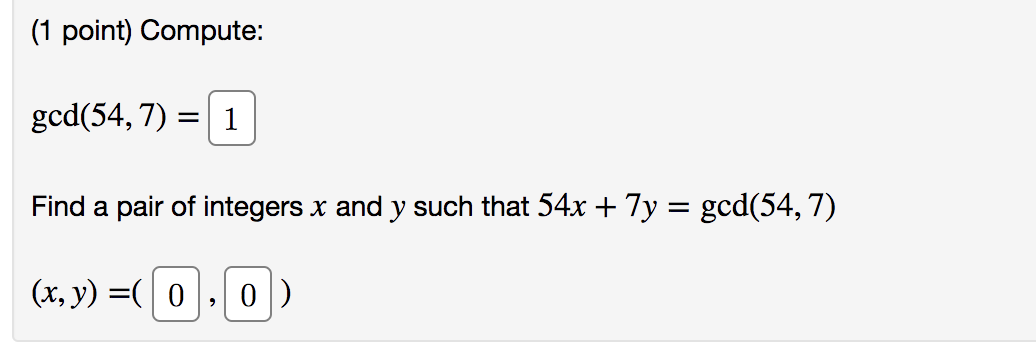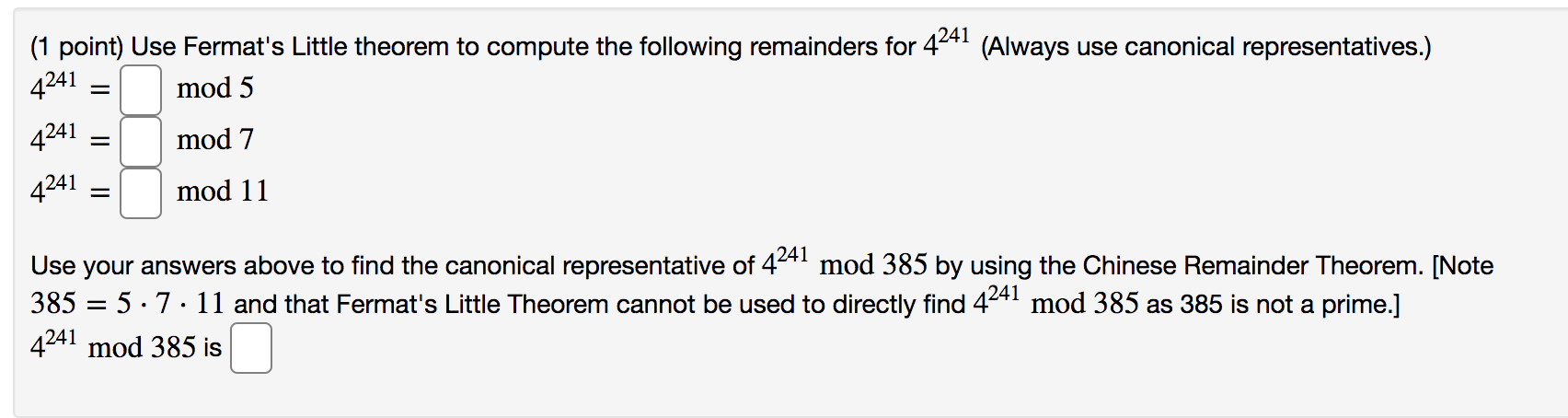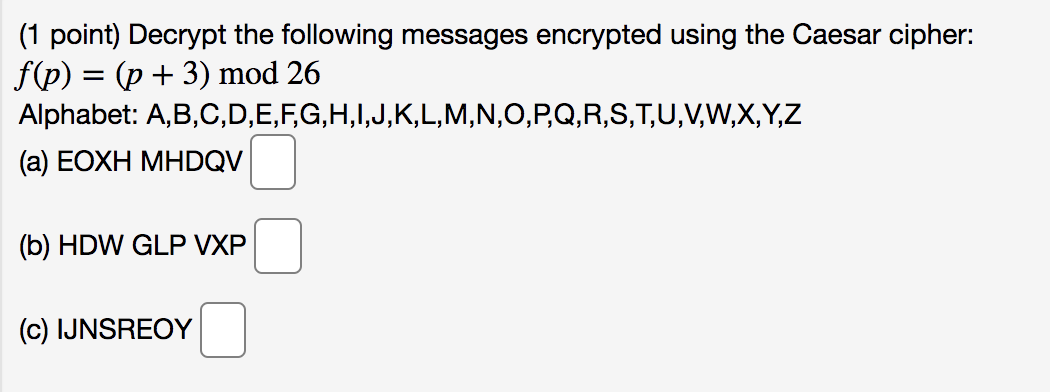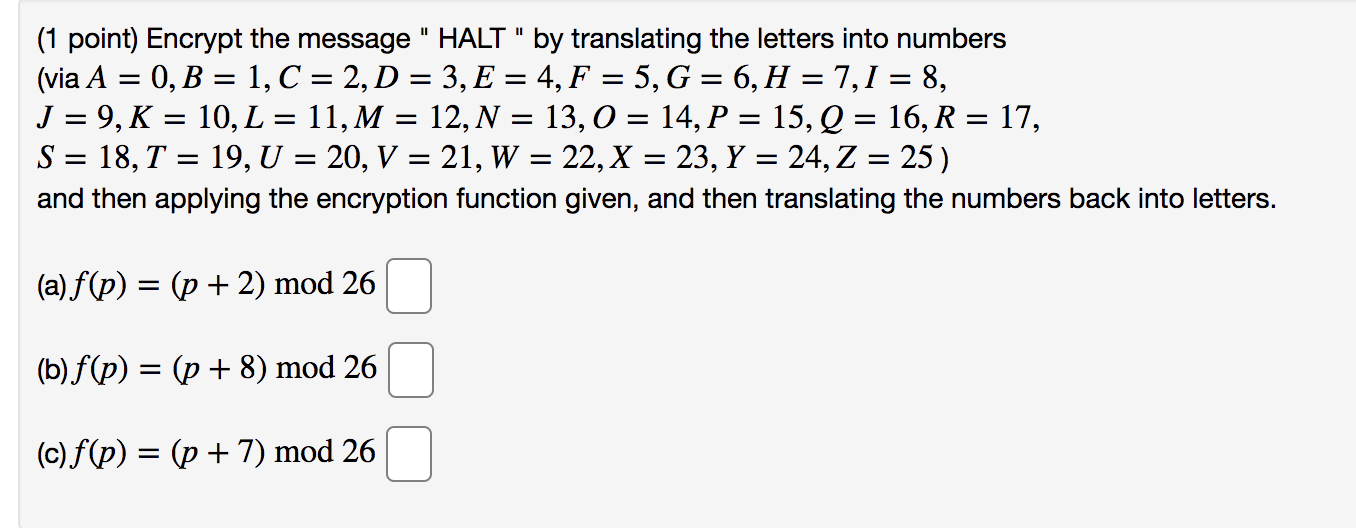
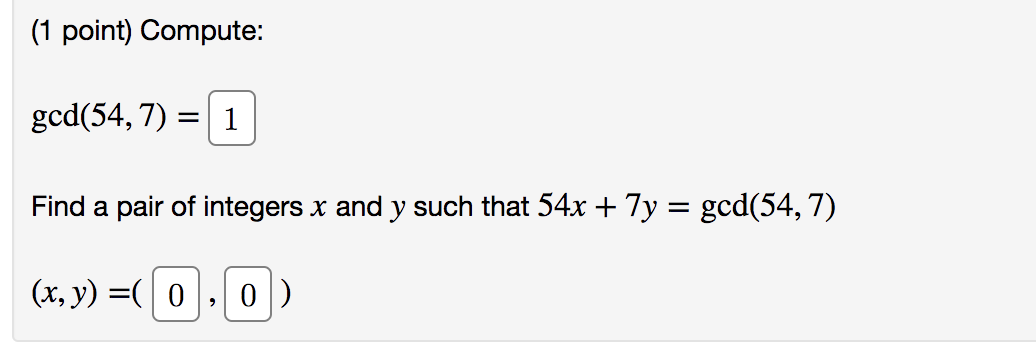




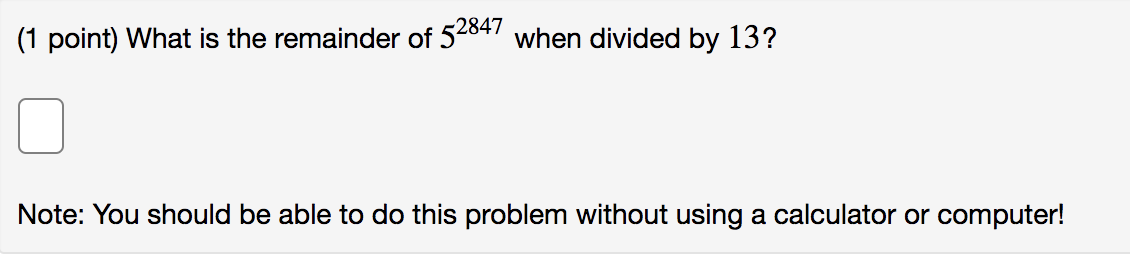
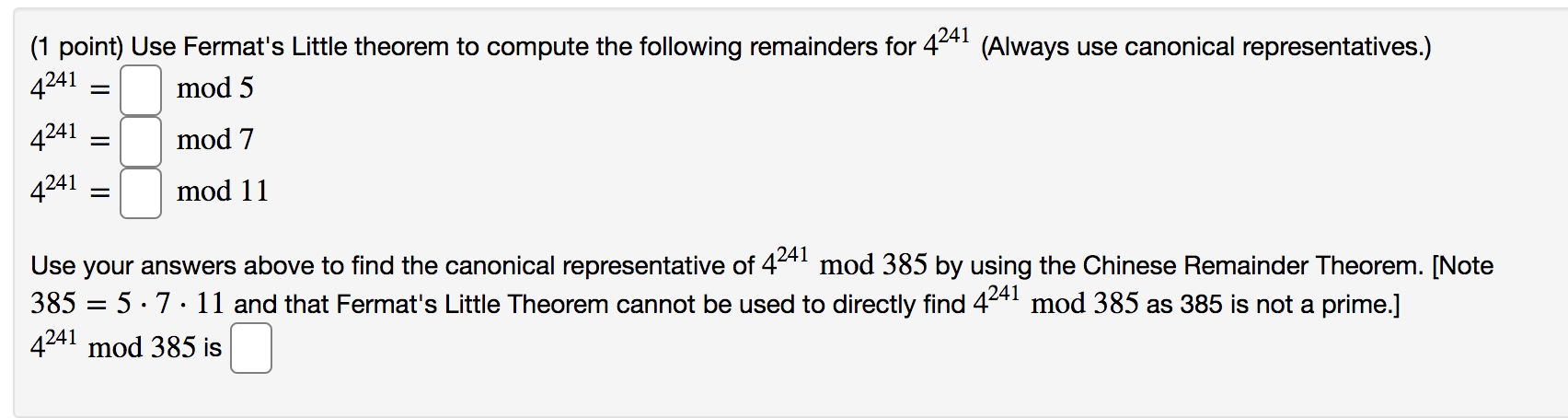
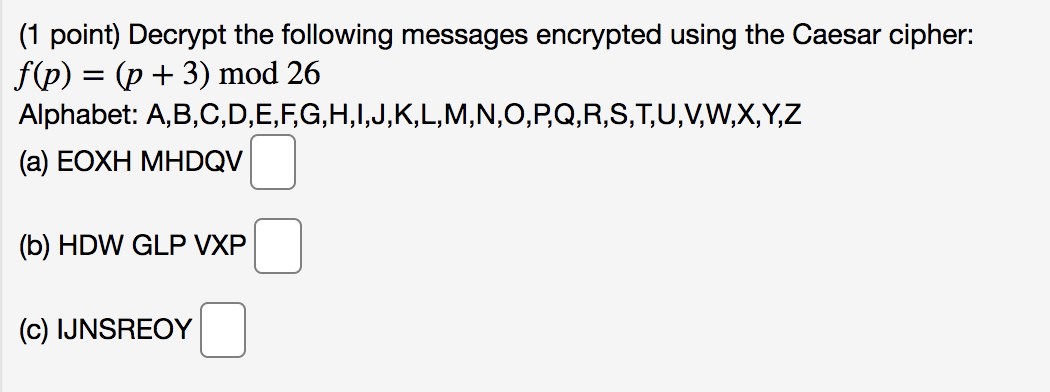




pleaseanswerthese
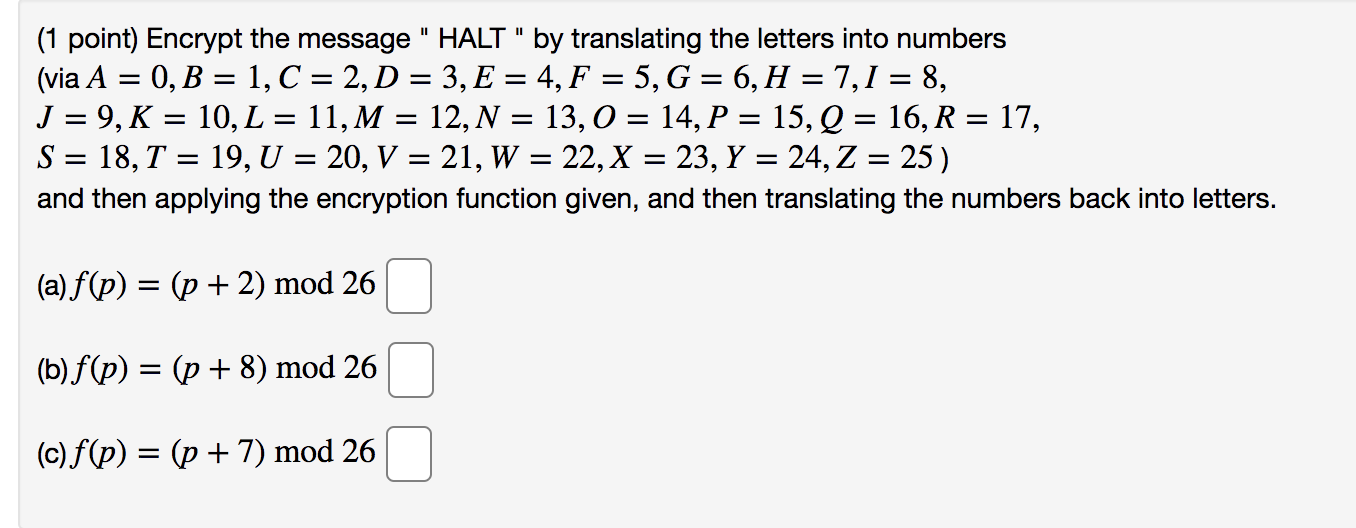
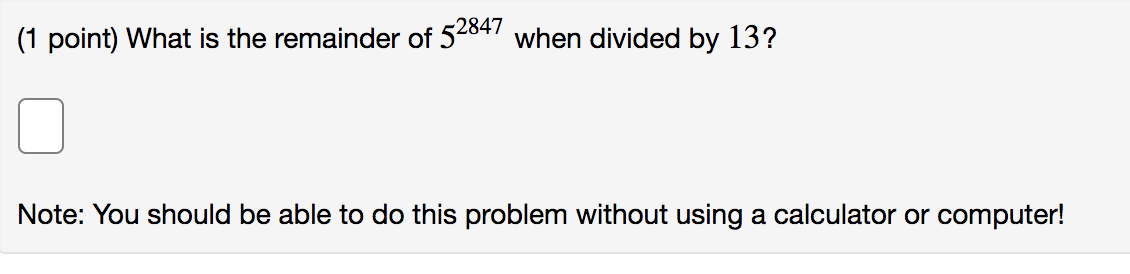
(1 point) Encrypt the message " HALT " by translating the letters into numbers (via A = 0, B = 1, C = 2, D = 3, E = 4, F = 5, G = 6, H = 7, 1 = 8, J = 9, K = 10, L = 11, M = 12, N = 13, 0 = 14, P = 15, Q = 16, R = 17, S = 18, T = 19, U = 20, V = 21, W = 22, X = 23, Y = 24, Z = 25 ) and then applying the encryption function given, and then translating the numbers back into letters. (a) f(p) = (p + 2) mod 26 (b) f(p) = (p+ 8) mod 26 (c) f(p) = (p + 7) mod 26(1 point) Compute: gcd(54, 7) = 1 Find a pair of integers x and y such that 54x + 7y = god(54, 7) (x, y) = 0 0(1 point) The goal of this exercise is to practice finding the inverse modulo m of some (relatively prime) integer n. We will find the inverse of 9 modulo 38, i.e., an integer c such that 90 E 1 (mod 38). First we perform the Euclidean algorithm on 9 and 38: 38:92: +C] C]: *4+1 [Note your answers on the second row should match the ones on the first row.] Thus gcd(9,38)=1, i.e., 9 and 38 are relatively prime. Now we run the Euclidean algorithm backwards to write 1 = 38s + 91' for suitable integers s, t. s = t = when we look at the equation 38s + 91' E 1 (mod 38), the multiple of 38 becomes zero and so we get 91' E 1 (mod 38). Hence the multiplicative inverse of 9 modulo 38 is C] (1 point) Solve the following congruence. Make sure that the number you enter is in the range [0, M 1] where M is the modulus of the congruence. 400x = 1 (mod 627) x=D ('I point) Find the smallest positive integer solution to the following system of congruence: x E 6 (mod 18) E 5 (mod 7) no (1 point) Find the smallest positive integer solution to the following system of congruence: x E 4 (mod 13) E 7 (mod 19) E 5 (mod 10) no (1 point) What is the remainder of 52847 when divided by 13? Note: You should be able to do this problem without using a calculator or computer!(1 point) Use Fermat's Little theorem to compute the following remainders for 4241 (Always use canonical representatives.) 4241 = mod 5 4241 = mod 7 4241 = mod 11 4241 mod 385 by using the Chinese Remainder Theorem. [Note Use your answers above to find the canonical representative of 4241 mod 385 as 385 is not a prime.] 385 = 5 - 7 - 11 and that Fermat's Little Theorem cannot be used to directly find 4241 mod 385 is C] (1 point) Decrypt the following messages encrypted using the Caesar cipher: f(p) = (p + 3) mod 26 Alphabet: A,B,C,D,E,F,G, H,I,J,K,L,M,N,O,P,Q,R,S, T,U,V,W,X, Y,Z (a) EOXH MHDQV (b) HDW GLP VXP (c) IJNSREOY(1 point) The goal of this exercise is to work thru the RSA system in a simple case: We will use primesp = 47, q = 43 and form n = 47 - 43 = 2021. [This is typical of the RSA system which chooses two large primes at random generally, and multiplies them to find n. The public will know n but p and q will be kept private] Now we choose our public key 6 = 13. This will work since gcd(13, (p 1)(q 1)) = gcd(13, 1932) = 1. [In general as long as we choose an 'e' with gcd(e,(p-1)(q-'l))=1, the system will work.] Next we encode letters of the alphabet numerically say via the usual: (A=0,B=1,C=2,D=3,E=4,F=5,G=6,H=7,|=8, J=9,K=1U,L=11,M=12,N=13,0=14,P=15,Q=16,R=17, S=1B,T=19,U=20,V=21,W=22,X=23,Y=24,Z=25.) We will practice the RSA encryption on the single integer 15. (which is the numerical representation for the letter "P\"). In the language of the book, M=15 is our original message. The coded integer is formed via c = M E mod n. Thus we need to calculate 1513 mod 2021. This is not as easy as it seems and you might consider using fast modular multiplication The canonical representative of 1513 mod 2021 is C] (1 point) We will find the smallest positive integer x that solves the following system of congruences via the Chinese Remainder Theorem: x= 1 mod 3 x = 2 mod 5 x = 4 mod 7 x = 8 mod 43 In the language of Theorem 4 from page 236 of the 6th edition of Rosen, we thus have the values of the following variables: a1 = 1 and m1 = 3 a2 = 2 and m2 = 5 a3 = 4 and m3 = 7 a4 = 8 and m4 = 43 The first step is to calculate m = mim2mm4. When we do this we get: m = The second step is to calculate the mx which are given by the formula mk = m . Enter their values below: m1 = my = iz = MA = Next we find the yx which are given by solving yumx = 1 mod mk Thus for example, to find y, we need to solve 1505y, = 1 mod 3Since we know 1505 E 2 mod 3, this simplifies to 2511 E 1 mod 3 Solve this either by trial and error or by using the Euclidean algorithm and enter the value of ll below: (Use the canonical representative modulo 3.) 3'1 = C] Similarly, to find 512 we need to solve 903322 E 1 mod 5 Since we know 903 E 3 mod 5,this simplifies to 3312 E 1mod5 Solve this either by trial and error or by using the Euclidean algorithm and enter the value of 372 below: (Use the canonical representative modulo 5-) 3'2 = C] Similarly, to find 513 we need to solve 645373 E 1 mod 7 Since we know 645 E 1 mod 7,this simplifies to 1573 E 1m0d7 Solve this either by trial and error or by using the Euclidean algorithm and enter the value of 3'3 below: (Use the canonical representative modulo 7.) 93= Similarly, to find 374 we need to solve 105524 E 1 mod 43 Since we know 105 E 19 mod 43,this simplifies to 19334 E 1 mod 43 Solve this either by trial and error or by using the Euclidean algorithm and enter the value of 574 below: (Use the canonical representative modulo 43.) 314 = C] Now that we have all the ak, u and 31k, use the formula x = 2L1 aktkj'lk to find an integer solution x to the original system. The Chinese remainder theorem says that this x and any integer congruent modulo m to it, will solve the original system. Enter the SMALLEST positive integer solution to the original system here: C]