pleass do not use excel show me how !solvet by hand Place a circle next to the answer thank you

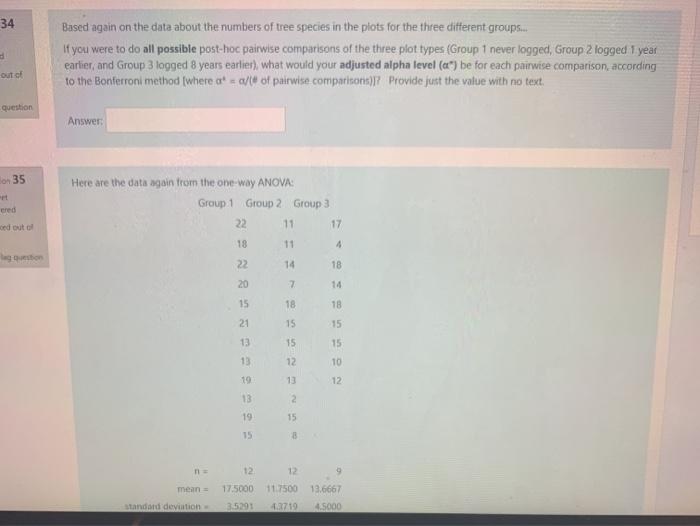
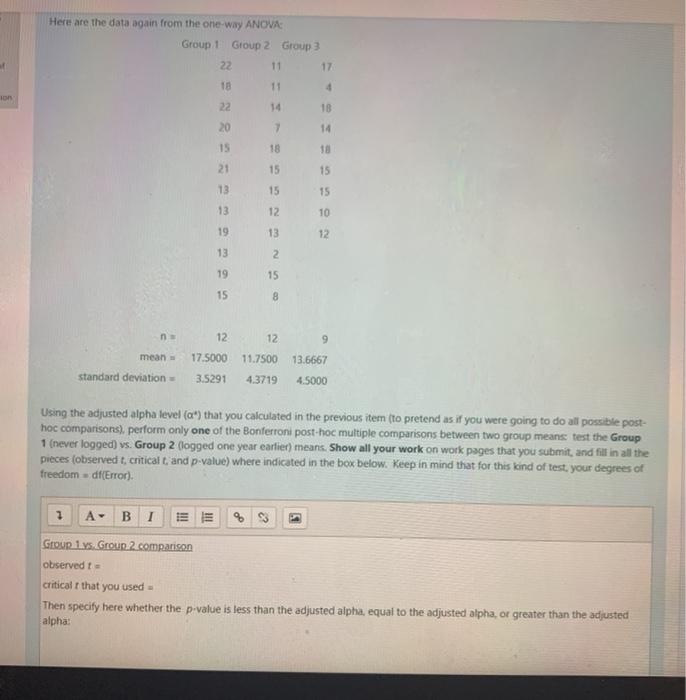
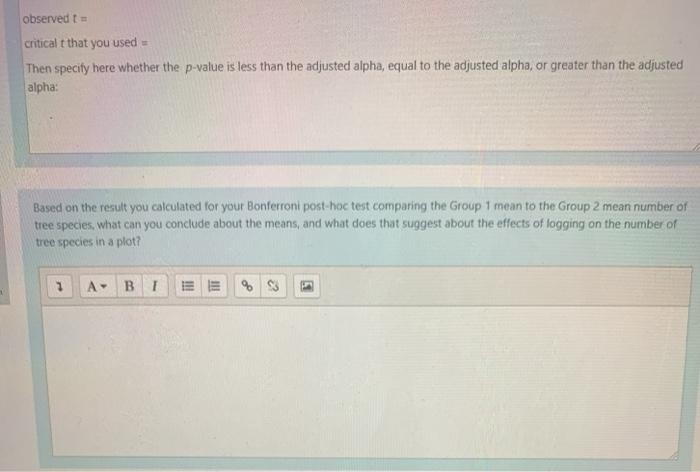
34 Based again on the data about the numbers of tree species in the plots for the three different groups. If you were to do all possible post-hoc pairwise comparisons of the three plot types (Group I never logged, Group 2 logged 1 year earlier and Group 3 logged 8 years earlier), what would your adjusted alpha level (a") be for each pairwise comparison, according to the Bonferroni method (where are = a/e of pairwise comparisons)? Provide just the value with no text. out of question Answer: on 35 Here are the data again from the one-way ANOVA: Group 1 Group 2 Group 3 22 11 17 ered od out 18 11 4 ago 22 14 18 20 7 14 15 18 18 21 15 15 13 15 15 13 12 10 19 13 12 2 13 19 15 15 8 12 12 mean 17.5000 11.7509 12719 13.6667 4.5000 Standard deviation 3.5291 Here are the data again from the one-way ANOVA Group 1 Group 2 Group 3 22 11 17 18 11 4 10 22 14 18 20 7 14 15 18 21 15 15 13 15 15 13 12 10 19 13 12 13 2 19 15 15 8 n 12 12 9 mean 11.7500 13.6667 17.5000 3.5291 standard deviation 4.3719 4.5000 Using the adjusted alpha level (a") that you calculated in the previous item (to pretend as if you were going to do all possible post- hoc comparisons), perform only one of the Bonferroni post-hoc multiple comparisons between two group means test the Group 1 (never logged) vs. Group 2 (logged one year earlier) means. Show all your work on work pages that you submit, and fill in all the pieces (observed t, critical t, and p-value) where indicated in the box below. Keep in mind that for this kind of test your degrees of freedom = df(Error) A. B I Group 1 vs. Groun 2.comparison observed to critical that you used Then specify here whether the p-value is less than the adjusted alpha, equal to the adjusted alpha, or greater than the adjusted alpha: observed to critical t that you used = Then specify here whether the p-value is less than the adjusted alpha, equal to the adjusted alpha, or greater than the adjusted alpha Based on the result you calculated for your Bonferroni post-hoc test comparing the Group 1 mean to the Group 2 mean number of tree species, what can you conclude about the means, and what does that suggest about the effects of logging on the number of tree species in a plot? BI HII 11! %3 34 Based again on the data about the numbers of tree species in the plots for the three different groups. If you were to do all possible post-hoc pairwise comparisons of the three plot types (Group I never logged, Group 2 logged 1 year earlier and Group 3 logged 8 years earlier), what would your adjusted alpha level (a") be for each pairwise comparison, according to the Bonferroni method (where are = a/e of pairwise comparisons)? Provide just the value with no text. out of question Answer: on 35 Here are the data again from the one-way ANOVA: Group 1 Group 2 Group 3 22 11 17 ered od out 18 11 4 ago 22 14 18 20 7 14 15 18 18 21 15 15 13 15 15 13 12 10 19 13 12 2 13 19 15 15 8 12 12 mean 17.5000 11.7509 12719 13.6667 4.5000 Standard deviation 3.5291 Here are the data again from the one-way ANOVA Group 1 Group 2 Group 3 22 11 17 18 11 4 10 22 14 18 20 7 14 15 18 21 15 15 13 15 15 13 12 10 19 13 12 13 2 19 15 15 8 n 12 12 9 mean 11.7500 13.6667 17.5000 3.5291 standard deviation 4.3719 4.5000 Using the adjusted alpha level (a") that you calculated in the previous item (to pretend as if you were going to do all possible post- hoc comparisons), perform only one of the Bonferroni post-hoc multiple comparisons between two group means test the Group 1 (never logged) vs. Group 2 (logged one year earlier) means. Show all your work on work pages that you submit, and fill in all the pieces (observed t, critical t, and p-value) where indicated in the box below. Keep in mind that for this kind of test your degrees of freedom = df(Error) A. B I Group 1 vs. Groun 2.comparison observed to critical that you used Then specify here whether the p-value is less than the adjusted alpha, equal to the adjusted alpha, or greater than the adjusted alpha: observed to critical t that you used = Then specify here whether the p-value is less than the adjusted alpha, equal to the adjusted alpha, or greater than the adjusted alpha Based on the result you calculated for your Bonferroni post-hoc test comparing the Group 1 mean to the Group 2 mean number of tree species, what can you conclude about the means, and what does that suggest about the effects of logging on the number of tree species in a plot? BI HII 11! %3