Answered step by step
Verified Expert Solution
Question
1 Approved Answer
pls zoom up to read... it posts blurry idk why but will like!! for part b it asks for yearly % monthly % and daily
pls zoom up to read... it posts blurry idk why but will like!! 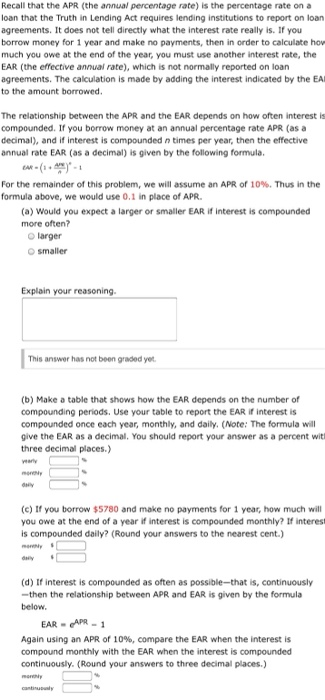

for part b it asks for yearly % monthly % and daily %
Recall that the APR (the annual percentage rate) is the percentage rate on a loan that the Truth in Lending Act requires lending institutions to report on loan agreements. It does not tell directly what the interest rate really is. If you borrow money for 1 year and make no payments, then in order to calculate hov much you owe at the end of the year, you must use another interest rate, the EAR (the effective annual rate), which is not normally reported on loan agreements. The calculation is made by adding the interest indicated by the EA to the amount borrowed. The relationship between the APR and the EAR depends on how often interest is compounded. If you borrow money at an annual percentage rate APR (as a decimal), and if interest is compounded n times per year, then the effective annual rate EAR (as a decimal) is given by the following formula. For the remainder of this problem, we will assume an APR of 10%. Thus in the formula above, we would use 0.1 in place of APR. (a) Would you expect a larger or smaller EAR If interest is compounded more often? larger smaller Explain your reasoning This answer has not been graded yet (b) Make a table that shows how the EAR depends on the number of compounding periods. Use your table to report the EAR if interest is compounded once each year, monthly, and daily. (Note: The formula will give the EAR as a decimal. You should report your answer as a percent wit three decimal places.) va (e) If you borrow $5780 and make no payments for 1 year, how much will you owe at the end of a year if interest is compounded monthly? If interest is compounded daily? (Round your answers to the nearest cent.) (d) If interest is compounded as often as possible--that is, continuously -then the relationship between APR and EAR is given by the formula below. EAR-APR-1 Again using an APR of 10%, compare the EAR when the interest is compound monthly with the EAR when the interest is compounded continuously. (Round your answers to three decimal places.) part c asks for monthly and daily how much you owe and part d is monthly % and continuously %
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


