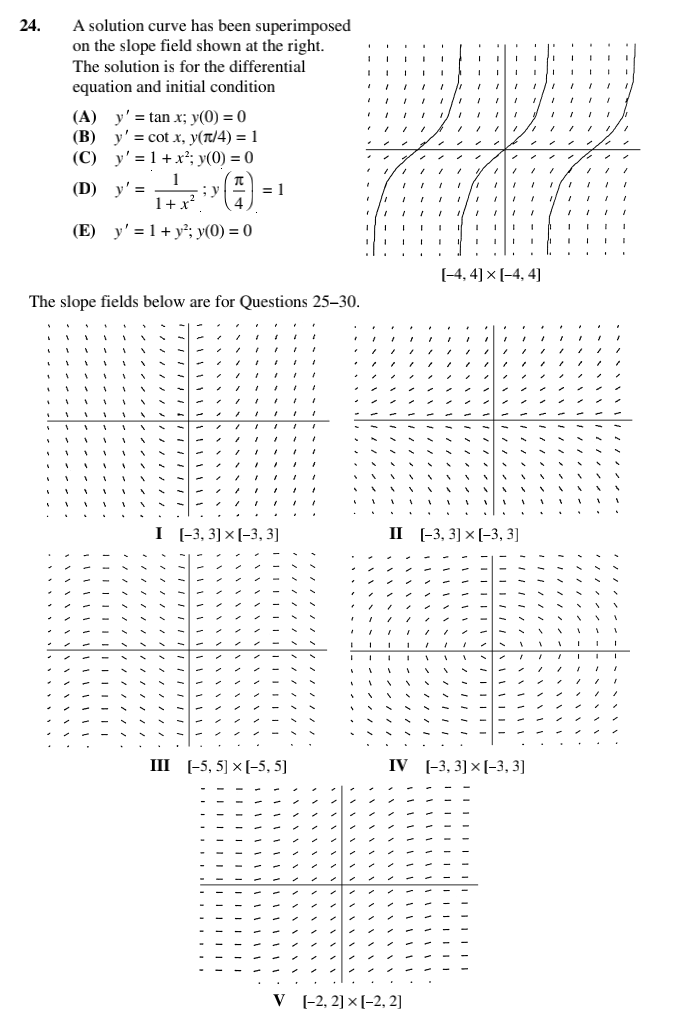
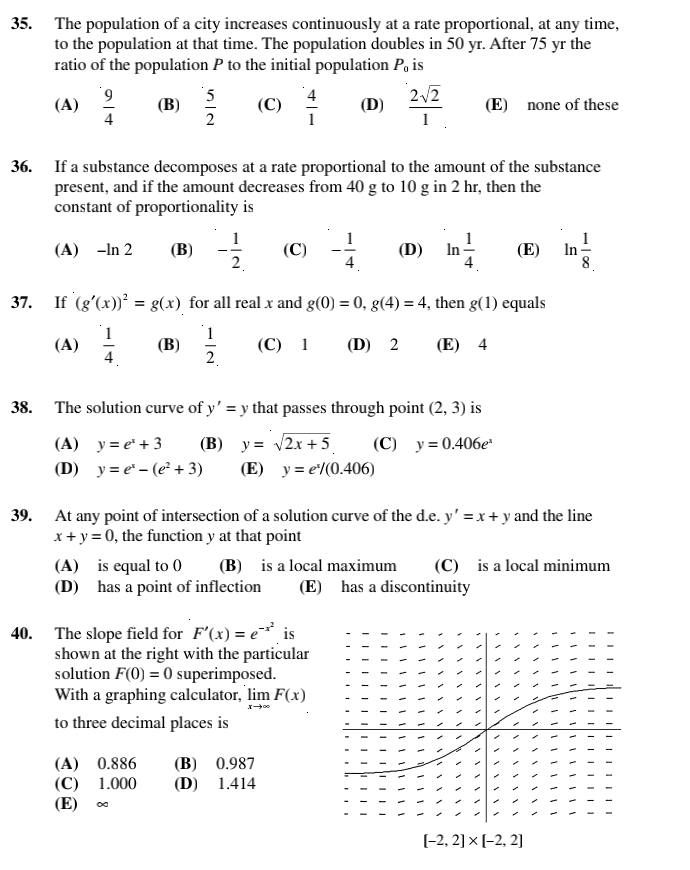
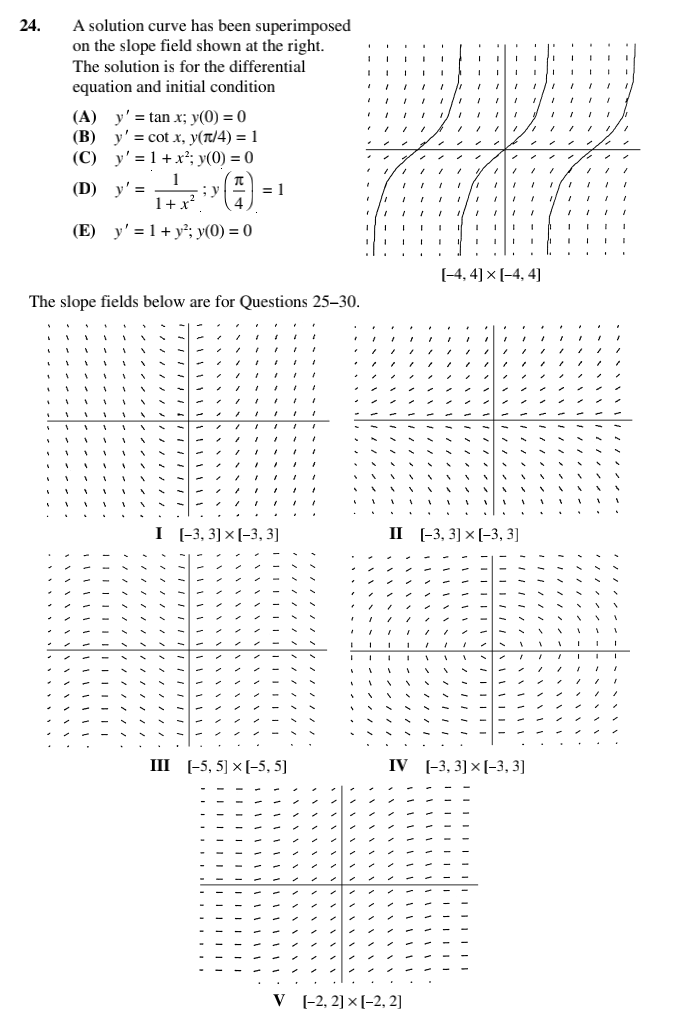
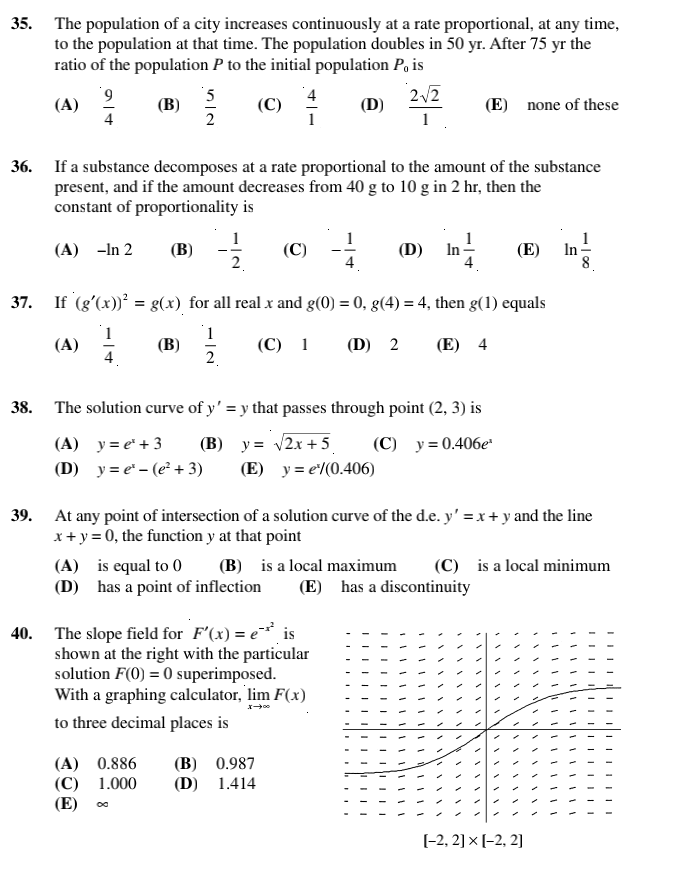
Practice Exercises Part A. Directions: Answer these questions without using your calculator. In Questions 1-10, a(t) denotes the acceleration function, v(t) the velocity function, and s(t) the position or height function at time t. (The acceleration due to gravity is -32 ft/sec'.) 1. If a(t) = 4t - 1 and v(1) = 3, then v(t) equals (A) 212 - t (B) 212 -1+ 1 (C) 212 -1+ 2 (D) 212 + 1 (E) 212 + 2 2. If a(t) = 2013 - 6t, s(-1) = 2, and s(1) = 4, then v(t) equals (A) t-t (B) 514 - 313 + 1 (C) 514 - 312 + 3 (D) t-13 + 1+ 3 (E) +-13+1 3. Given a(t), s(-1), and s(1) as in Question 2, then s(0) equals (A) 0 (B) 1 (C) 2 (D) 3 (E) 4. A stone is thrown straight up from the top of a building with initial velocity 40 ft/sec and hits the ground 4 sec later. The height of the building, in feet, is (A) 88 (B) 96 (C) 112 (D) 128 (E) 144 5. The maximum height is reached by the stone in Question 4 after (A) 4/5 sec (B) 4 sec (C) 5/4 sec (D) 5/2 sec (E) 2 sec 6. If a car accelerates from 0 to 60 mph in 10 sec, what distance does it travel in those 10 sec? (Assume the acceleration is constant and note that 60 mph = 88 ft/sec.) (A) 40 ft (B) 44 ft (C) 88 ft (D) 400 ft (E) 440 ft . A stone is thrown at a target so that its velocity after t sec is (100 - 20t) ft/sec. If the stone hits the target in 1 sec, then the distance from the sling to the target is (A) 80 ft (B) 90 ft (C) 100 ft (D) 110 ft (E) 120 ft 8. What should the initial velocity be if you want a stone to reach a height of 100 ft when you throw it straight up? (A) 80 ft/sec (B) 92 ft/sec (C) 96 ft/sec (D) 112 ft/sec (E) none of these16. The general solution of the differential equation x dy = y dx is a family of (A) circles (B) hyperbolas (C) parallel lines (D) parabolas (E) lines passing through the origin 17. The general solution of the differential equation dy = y is a family of (A) parabolas (B) straight lines (C) hyperbolas (D) ellipses (E) none of these 18. A function f(x) that satisfies the equations f(x)f'(x) = x and f(0) = 1 is (A) f( x) = Vx' +1 (B) f (x) = VI-x' (C) f( x) =x (D) f(x) =ex (E) none of these 19. The curve that passes through the point (1, 1) and whose slope at any point (x, y) is equal to 2 has the equation (A) 3x - 2= y (B) y= x (C) y=x (D) 3y= = x2 +2 (E) 3yz - 2x = 1 20. What is the domain of the particular solution in Question 19? (A) all real numbers (B) x|$1 (C) x#0 (D) x0 21. If dx dy _ k k a constant, and if y = 2 when x = 1 and y = 4 when x = e, then, when X x = 2, y equals (A) 2 (B) 4 (C) In 8 (D) In2+2 (E) In 4+2 22. The slope field shown at the right is for the differential equation (A) y'=x+1 (B) y' = sin x (C) y' = -sin x (D) y' = COS X (E) y'=-COS X [-2n, 2x] x [-1.5, 1.5] 23. The slope field at the right is for the differential equation (A) y' = 2x (B) y' = 2x -4 (C) y' =4-2x (D) y'= y (E) y'=xty [-4, 4] x [-12, 12]24. A solution curve has been superimposed on the slope field shown at the right. The solution is for the differential equation and initial condition (A) y' = tan x; y(0) = 0 (B) y' = cot x, y(1/4) = 1 (C) y'= 1+x; y(0) =0 (D) y'= 4 : 1 (E) y' = 1+ y; >(0) = 0 [-4, 4] x [-4, 4] The slope fields below are for Questions 25-30. [-3, 3] x [-3, 3] II [-3, 3] x [-3, 3] III [-5, 5] x [-5, 5] IV [-3, 3] x [-3, 3] V [-2, 2] x [-2, 2]25. Which slope field is for the differential equation y' = y? (A) I (B) II (C) III (D) IV (E) V 26. Which slope field is for the differential equation y' = - _ (A) I (B) II (C) III (D) IV (E) V 27. Which slope field is for the differential equation y' = sin x? (A) I (B) II (C) III (D) IV (E) V 28. Which slope field is for the differential equation y' = 2x? (A) I (B) II (C) III (D) IV (E) V 29. Which slope field is for the differential equation y' = e-? (A) I (B) II (C) III (D) IV (E) V 30. A particular solution curve of a differential equation whose slope field is shown above in II passes through the point (0,-1). The equation is (A) y=-e (B) y=-0- (C) y=x- 1 (D) y=-cos x (E) y= -VI-x'Part B. Directions: Some of the following questions require the use of a graphing calculator. 33. If ds = sin di S and if s = 1 when / = 0, then, when $ = , t is equal to (A) (B) (C) 1 (D) (E) IN 34. If radium decomposes at a rate proportional to the amount present, then the amount R left after t yr, if Ro is present initially and c is the negative constant of propor- tionality, is given by (A) R = Ract (B) R= Roe" (C) R = Rot 2 (D) R= Re (E) R= Rita35. The population of a city increases continuously at a rate proportional, at any time, to the population at that time. The population doubles in 50 yr. After 75 yr the ratio of the population P to the initial population Po is (A) (B) (C) (D) 2V2 NIU (E) none of these 36. If a substance decomposes at a rate proportional to the amount of the substance present, and if the amount decreases from 40 g to 10 g in 2 hr, then the constant of proportionality is (A) -In 2 (B) NI - (C) (D) In (E) In 8 37. If (8'(x))= = g(x) for all real x and g(0) = 0, g(4) = 4, then g(1) equals (A) (B) NI - (C) 1 (D) 2 (E) 4 38. The solution curve of y' = y that passes through point (2, 3) is (A) y=e'+3 (B) y= v2x+5 (C) y = 0.406e* (D) y=e - (e'+ 3) (E) y= e/(0.406) 39. At any point of intersection of a solution curve of the d.e. y' = x + y and the line x + y =0, the function y at that point (A) is equal to 0 (B) is a local maximum (C) is a local minimum (D) has a point of inflection (E) has a discontinuity 40. The slope field for F'(x) = e-* is shown at the right with the particular solution F(0) = 0 superimposed. With a graphing calculator, lim F(x) to three decimal places is (A) 0.886 (B) 0.987 (C) 1.000 (D) 1.414 (E) [-2, 2] x [-2, 2]Acup of coffee at temperature 180F is placed on a table in a room at 68F. The d.e. forits temperature attime r is % =-O.ll(y68]; y(0) = 180. After 10 min the temperature (in \"F] of the coffee is (A) 96 (n) 100 (C) 105 (D) 110 (E) 115 Approximately how long does it take the temperature of the coffee in Question 41 to drop to 75F? (A) 10min (3) 15min (C) 18min (1)) 20min (E) 25min The concentration of a medication injected into the bloodstream drops at a rate pro- portional to the existing concentration. If the factor of proportionality is 30% per hour. in how many hours will the concentration be one-tenth of the initial concentration? I l I 2 (A) 3 (I!) 43 (C) 63 (D) .7; (E) noneofthese 49. According to Newton's law of cooling, the temperature of an object decreases at a rate proportional to the difference between its temperature and that of the surrounding air. Suppose a corpse at a temperature of 32"C arrives at a mortuary where the tem- perature is kept at 10"C. Then the differential equation satisfied by the temperature T of the corpse t hr later is (A) dT dT dT = -k(T - 10) (B) = k(T - 32) (C) = 32p-k di dT dT (D) =-KT(T - 10) (E) = KT(T - 32) di di 50. If the corpse in Question 49 cools to 27"C in 1 hr, then its temperature (in "C) is given by the equation (A) T= 22e .2051 (B) T = 10el. 163 (C) 7= 10 + 22e-0.258 (D) T= 32e-0.169 (E) 7=32 - 10-0.093