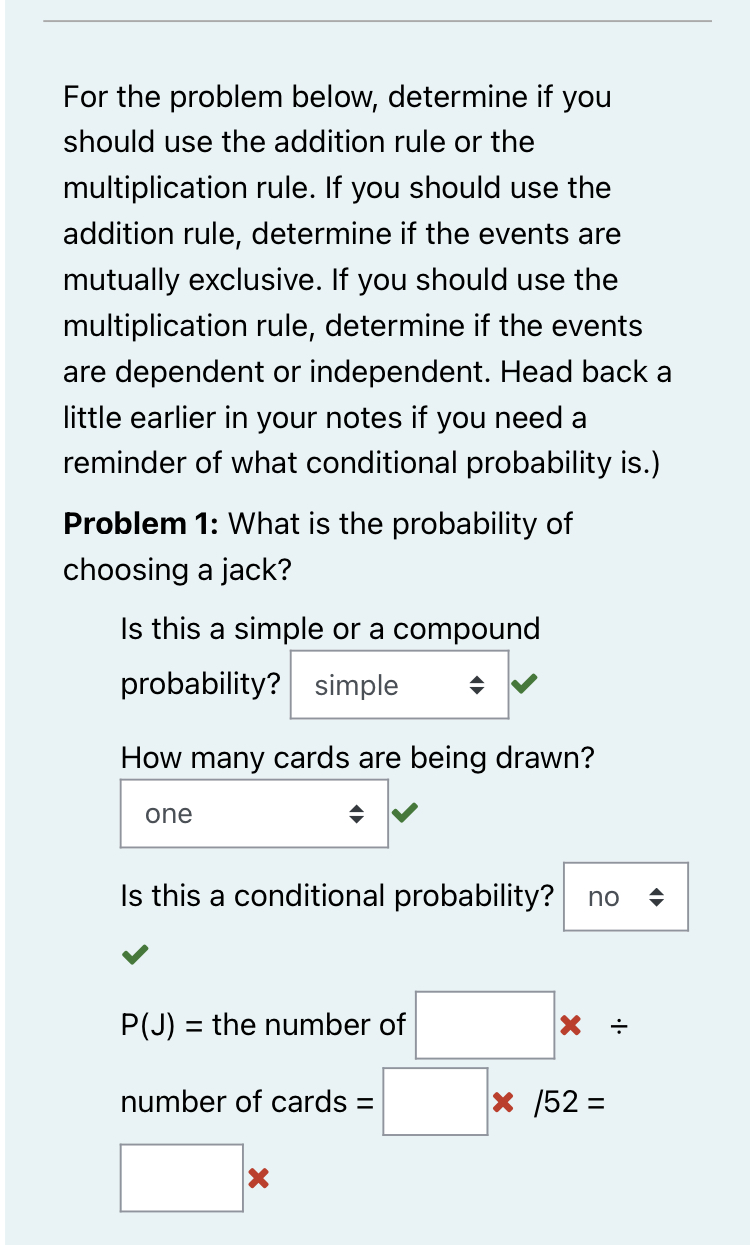
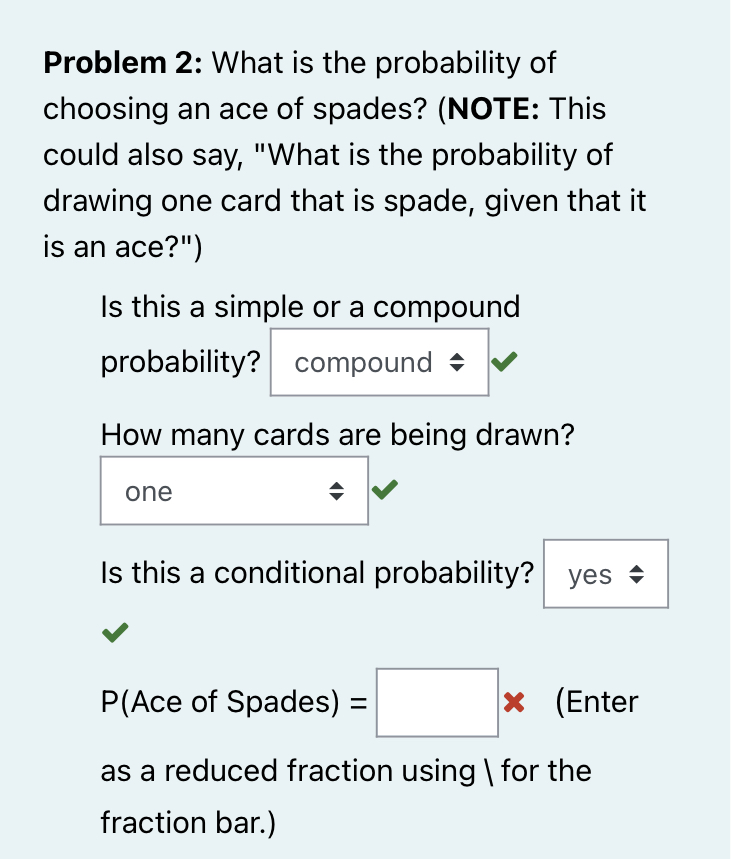
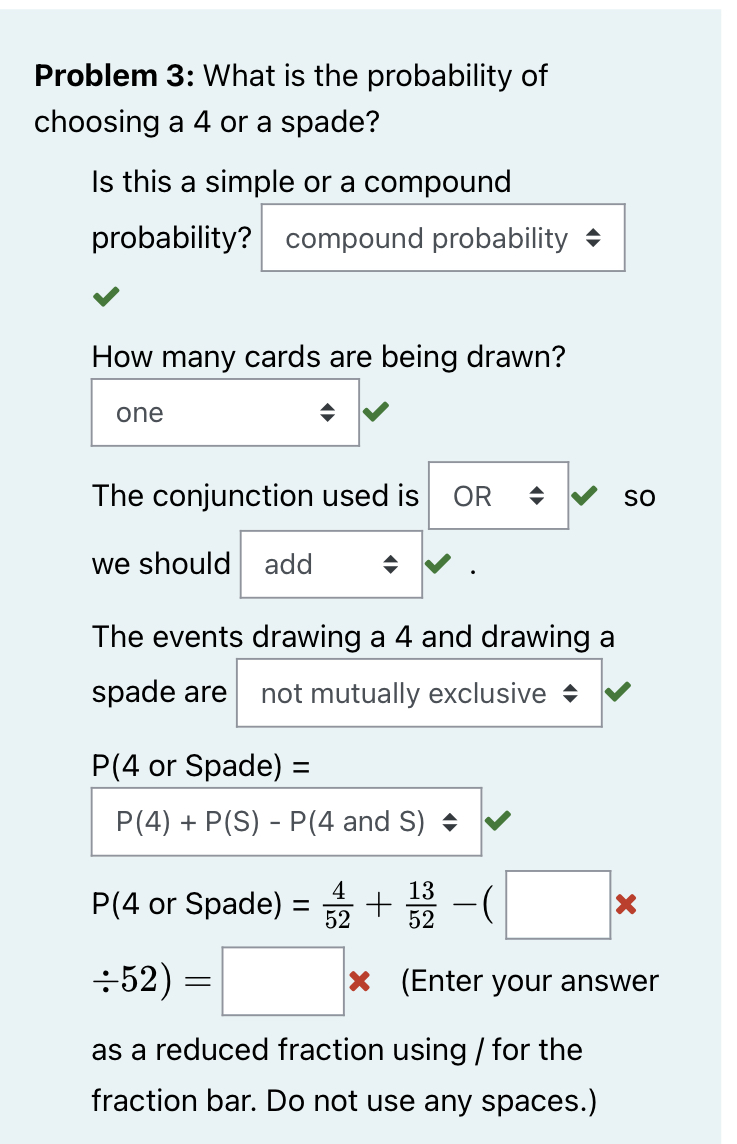
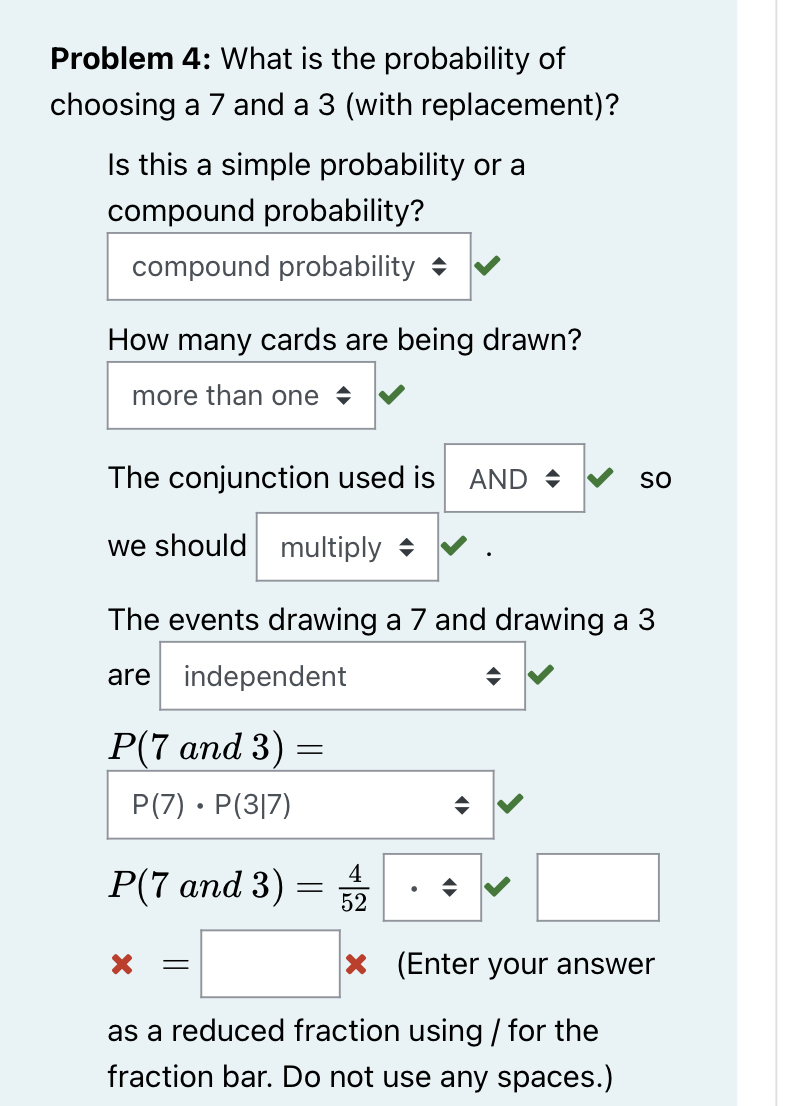
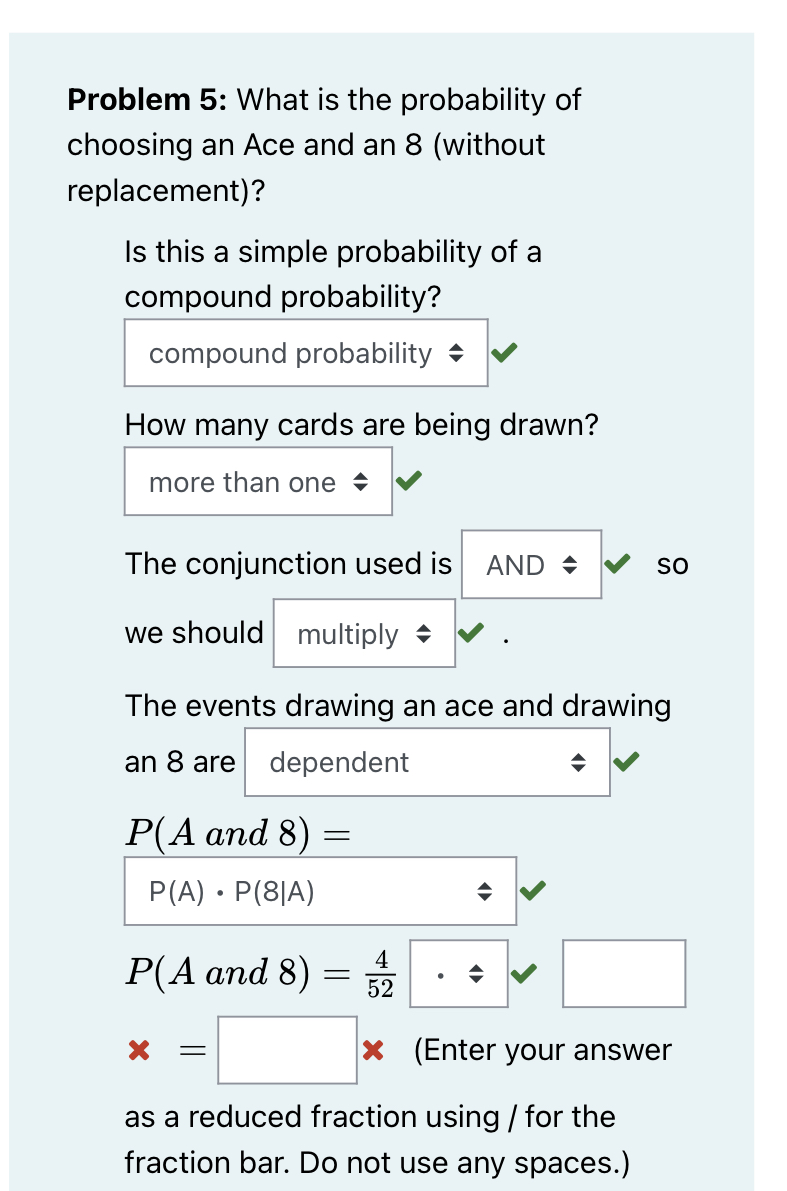
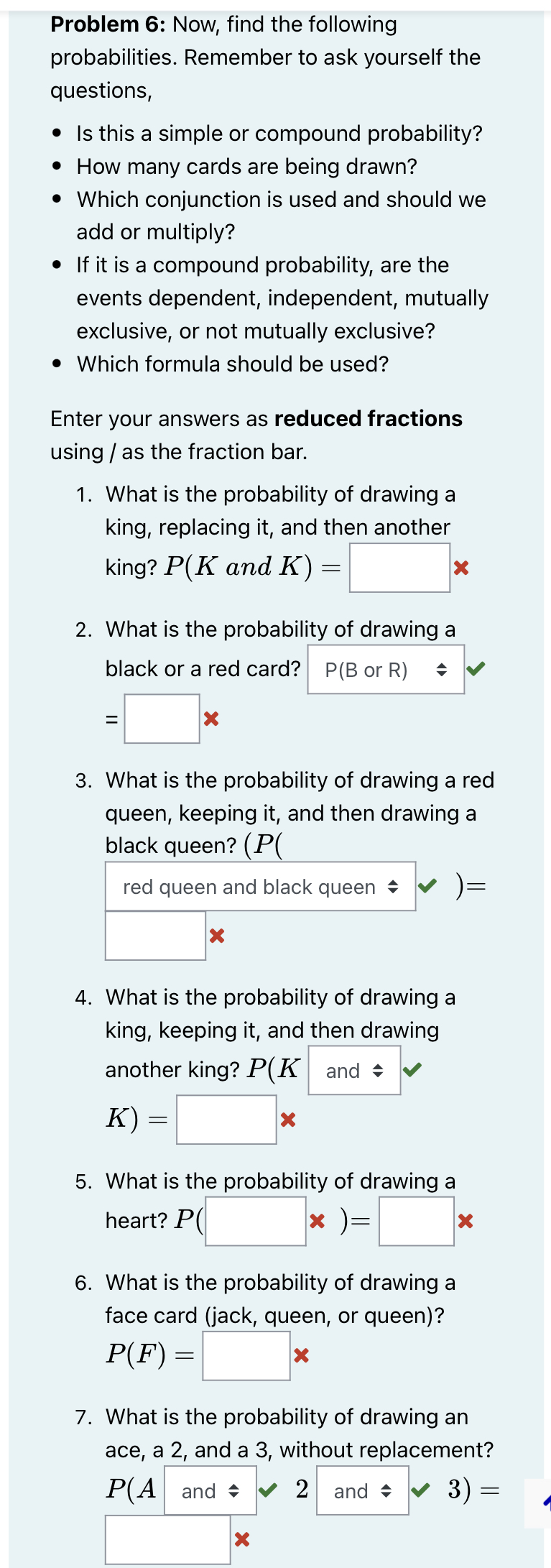
Practice Problem 2: Girl or Senior? A local high school has 1400 students; 800 of whom are girls. 300 of the students are seniors; of which 200 are girls. If we chose a student at random, what is the probability that we would choose a girl or a senior? Step 1: List the events. Event A: Choosing student who is a girl Event B: Choosing a student who is a senior Step 2: Decide if the events are mutually exclusive or not. The events are not mutually exclusive because one student can be a girl and a senior at the same time. Step 3: Write the correct equation and solve for the probability. The events are not mutually exclusive, so we should use the equation P(A or B) = P(A) + P(B) - P(A and B) because P(A and B) 0. How many total students attend the school? P(G or S) = P(G) + P(S) P(G and S) X students P(G or S) = 800 1400 P(G or S) = 200 1400 P(G or S) = 9 = 14 The probability of choosing a student who is a girl or a senior is 14. This means that 9 out of ever students is a girl, a senior, or both. The Addition Rule Practice Problems: Choosing 1 Item Use the Addition Rule to complete the following problems. - P(A or B) = P(A) + P(B) P(A and B) If the events are mutually exclusive P(A and B) = 0 Practice Problem 1: Christmas Ornaments Suppose you were given the following box of Christmas ornaments that contains 14 silver ornaments, 12 red ornament, and 8 green ornaments. What is the probability of randomly choosing a red or green ornament from the box? Step 1: List the events. Event A: Choosing a red ornament. Event B: Choosing a green ornament. Step 2: Decide if the events are mutually exclusive or not. = mutually exclusive because one solid colored The events are ornament cannot be red and green at the same time. 888 Step 3: Write the correct equation and solve for the probability. The events are mutually exclusive, so we should use the equation P(A or B) = P(A) + P(B) = P(A and B) = because P(A and B) = 0. How many total ornaments are in the box? 14 silver ornaments + 12 red ornaments + 8 green ornaments = 34 ornaments. P(R or G) = P(R) + P(G) P(R or G) = 12+ 34 20 P(R or G) 34 P(R or G)= This means that 10 ornament. out of every 17 ornaments in the box is a red or green Instructions: Determine if the following events are independent. Problem 1: Determine if events A and B are independent if P(A) = / P(B) = 3, and P(A and B) = 25 We learned that if events A and B are independent, P(B) = P(B|A). We are given that P(B) = . We need to find P(B|A). P(B|A) = P(A and B) P(A) 22 = 25 | 2 5 = = 25 P(B) = P(B|A) so the events are independent Problem 2: Determine if events A and 3 B are independent if P(A) = , 4' P(B) = 3 10' 1, and P(A and B) = = 3 40 If events A and B are independent, P(B) = P(B|A). We are given that P(B) = 3. We need to find P(B|A). P(B|A) = P(A and B) P(A) 10 3 = 40 4153 = P(B) = P(B|A) so the events are dependent Questions about probabilities often involve a deck of cards. Please become familiar with the cards that comprise a standard deck. A . 24 A % A A 2 * of of . J 9 g There are 52 cards in a deck. Twenty-six cards are black and 26 cards are red. The 52 cards can be broken down into four different suits; 13 hearts (), 13 diamonds (), 13 clubs (), and 13 spades Each card in a suit are labeled A (ace), 2-10, J (jack), Q (queen), and K (king). There are NO Jokers in a standard deck. Jacks, queens, and kings can also be called face cards. For the problem below, determine if you should use the addition rule or the multiplication rule. If you should use the addition rule, determine if the events are mutually exclusive. If you should use the multiplication rule, determine if the events are dependent or independent. Head back a little earlier in your notes if you need a reminder of what conditional probability is.) Problem 1: What is the probability of choosing a jack? Is this a simple or a compound probability? simple How many cards are being drawn? one Is this a conditional probability? no P(J) the number of = number of cards = /52 = Problem 2: What is the probability of choosing an ace of spades? (NOTE: This could also say, "What is the probability of drawing one card that is spade, given that it is an ace?") Is this a simple or a compound probability? compound = How many cards are being drawn? one Is this a conditional probability? yes P(Ace of Spades) = (Enter as a reduced fraction using \ for the fraction bar.) Problem 3: What is the probability of choosing a 4 or a spade? Is this a simple or a compound probability? compound probability How many cards are being drawn? one The conjunction used is OR we should add = The events drawing a 4 and drawing a spade are not mutually exclusive P(4 or Spade) = P(4) + P(S) P(4 and S) = P(4 or Spade) = 1 + 133 4 52 52 SO 52) = (Enter your answer as a reduced fraction using / for the fraction bar. Do not use any spaces.) Problem 4: What is the probability of choosing a 7 and a 3 (with replacement)? Is this a simple probability or a compound probability? compound probability How many cards are being drawn? more than one The conjunction used is AND we should multiply SO The events drawing a 7 and drawing a 3 are independent P(7 and 3) = P(7) P(317) P(7 and 3) 4 = 52 = (Enter your answer as a reduced fraction using / for the fraction bar. Do not use any spaces.) Problem 5: What is the probability of choosing an Ace and an 8 (without replacement)? Is this a simple probability of a compound probability? compound probability How many cards are being drawn? more than one The conjunction used is AND we should multiply SO The events drawing an ace and drawing an 8 are dependent P(A and 8): = P(A) P(8|A) P(A and 8) = 1 4 52 = (Enter your answer as a reduced fraction using / for the fraction bar. Do not use any spaces.) Problem 6: Now, find the following probabilities. Remember to ask yourself the questions, Is this a simple or compound probability? How many cards are being drawn? Which conjunction is used and should we add or multiply? If it is a compound probability, are the events dependent, independent, mutually exclusive, or not mutually exclusive? Which formula should be used? Enter your answers as reduced fractions using as the fraction bar. 1. What is the probability of drawing a king, replacing it, and then another king? P(K and K) - 2. What is the probability of drawing a black or a red card? P(B or R) = = 3. What is the probability of drawing a red queen, keeping it, and then drawing a black queen? (P( red queen and black queen )= 4. What is the probability of drawing a king, keeping it, and then drawing another king? P(K and K) = 5. What is the probability of drawing a heart? P( 6. What is the probability of drawing a face card (jack, queen, or queen)? P(F) = 7. What is the probability of drawing an ace, a 2, and a 3, without replacement? P(A and 2 and 3) = 8. What is the probability of drawing a Club or a 7? P(C or 7) = 9. What is the probability of drawing an ace, a 2 or a 3? P(A or 2 or 3): = Problem 3 Your cat had a litter of seven kittens. of the kittens are female and white, and 1 of the kittens are white. What is the probability that your cousin will choose a female kitten given that it is a white? P( ) Female and white White 47 37 34 34 ||