Probability Question

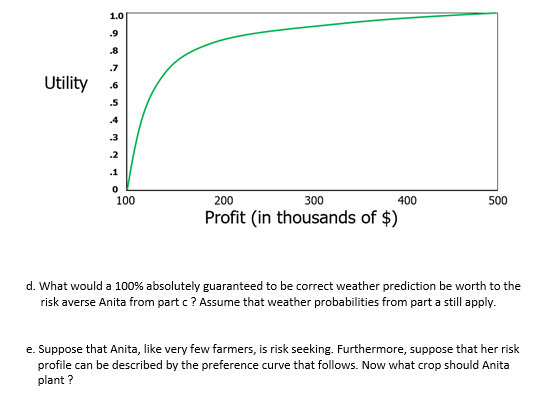
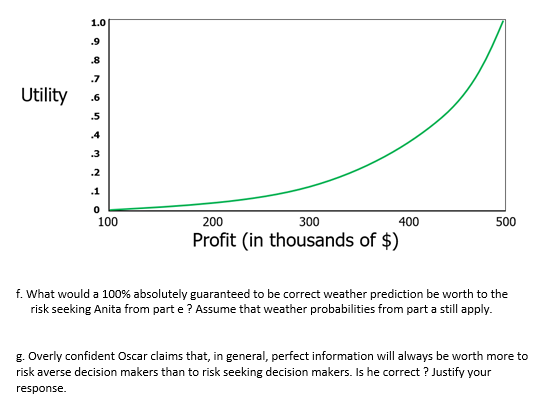
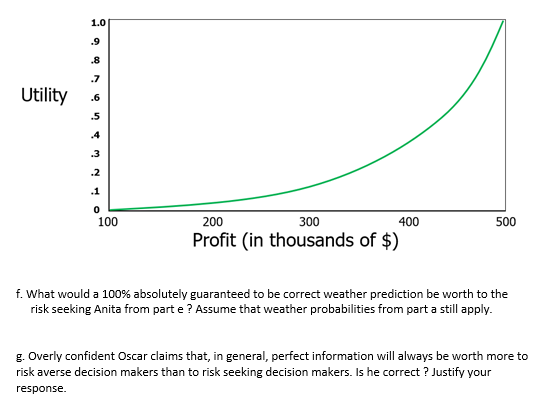
1. Your standard decision analysis question: Anita Cowpie operates a farm with 1000 acres of arable land. To keep things simple, she plants 1 cash crop each year, and rotates to a new crop the following season. Last year she planted crop D, so this year she is choosing whether to plant crop A, B, C, or E. Yields for each of the 4 crops will depend on prevailing weather conditions. Anita has estimated the crop yields and the profit that would be generated by each crop type (In $/acre) for 3 potential weather scenarios. The "Crop E" option actually represents the scenario where Anita chooses to plant a non harvestable cover crop, and then submits a crop insurance claim that guarantees a profit of $250/acre regardless of the weather conditions. All anticipated profits are shown in the table below: Anticipated Profit ($/Acre) Weather Pattern Crop A Crop B Crop C Crop E Dry 150 450 100 250 Moderate 500 300 300 250 Damp 150 200 450 250 Anita has studied the local weather patterns for years, so she knows that the likelihoods of the different weather patterns during the growing season are: P(dry weather)= .3; P(moderate weather) = .5; P(damp weather) = .2 a. Suppose Anita is an EMV decision maker. Which crop should she plant ? b. What would a 100% absolutely guaranteed to be correct weather prediction be worth to Anita if she is a EMV decision maker ? Assume that weather probabilities from part a still apply. c. Suppose that Anita, like many farmers, is risk averse. Furthermore, suppose that her risk profile can be described by the preference curve below. Now what crop should Anita plant ?1.0 9 Utility 100 200 300 400 500 Profit (in thousands of $) d. What would a 100% absolutely guaranteed to be correct weather prediction be worth to the risk averse Anita from part c ? Assume that weather probabilities from part a still apply. e. Suppose that Anita, like very few farmers, is risk seeking. Furthermore, suppose that her risk profile can be described by the preference curve that follows. Now what crop should Anita plant ?1.0 .9 Utility 100 200 300 400 500 Profit (in thousands of $) f. What would a 100% absolutely guaranteed to be correct weather prediction be worth to the risk seeking Anita from part e ? Assume that weather probabilities from part a still apply. g. Overly confident Oscar claims that, in general, perfect information will always be worth more to risk averse decision makers than to risk seeking decision makers. Is he correct ? Justify your response