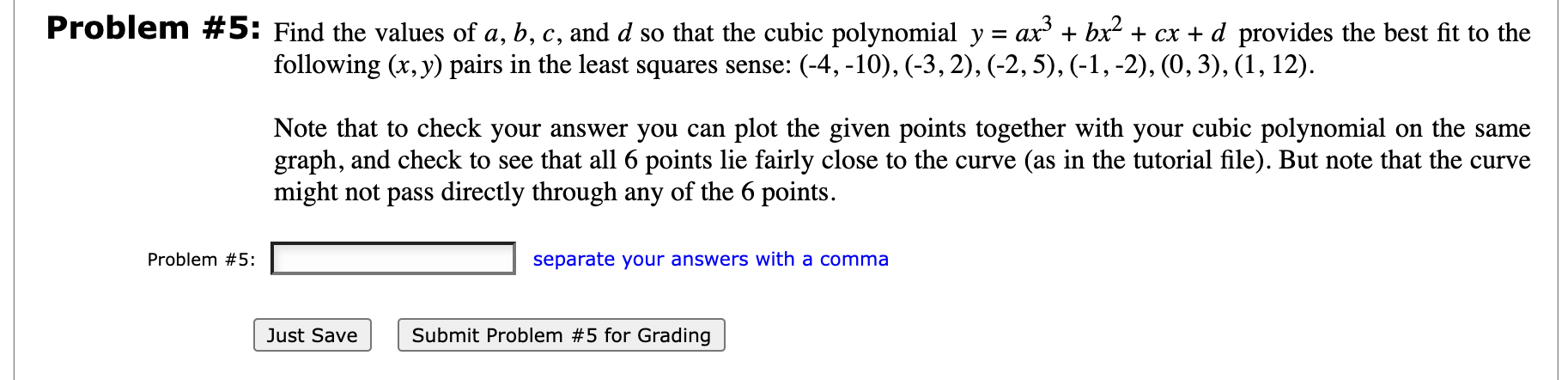
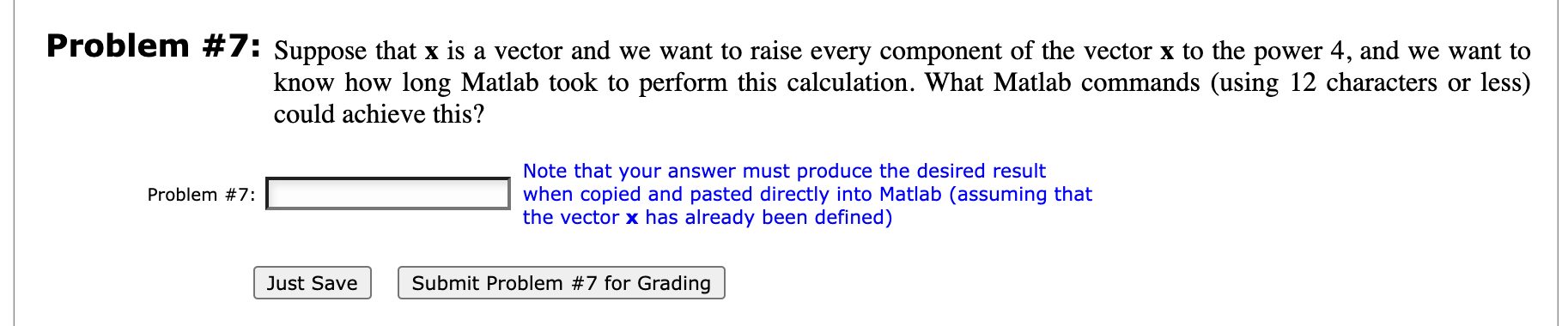
Problem #1: (a) Find the value of the following product: 4 9 14 Problem #1(a): Problem #1(b): Hint: Use the colon operator to produce the vector [4 9 14 ... 239], and then find the product of the elements of that vector. (b) Find the value of the following sum: 13 +21 + 29 + Just Save Submit Problem #1 for Grading Problem #1 Attempt #1 Your Answer: 1(a) 1(b) Your Mark: 1(a) 1(b) Attempt #2 1(a) 1(b) 1(a) 1(b) Attempt #3 1(a) 1(b) 239 1(a) 1(b) + 781 Problem #2: Consider the below matrix A, which you can copy and paste directly into Matlab. The matrix contains 3 columns, which represent the final grades in a course with 3 sections of equal size. The first column is C01, the second is CO2, and the third is C03. Problem #2(a): Problem #2(b): A = [72.69 32.58 100;57.02 89.79 96.67;15.93 35.49 46.95;73.98 100 63.66;63.45 86.99 47.45;23.98 93.73 87.19;100 64.94 31.27;29.41 56.31 23.67;71.89 100 100;100 81.11 31.08;66.54 91.22 80.57;57.2 10.91 90.74;94.32 16.76 74.21;55.25 100 50.76;95.16 76.03 23.8;84.55 93.9 96.33;42.95 100 53.02;100 53.23 80.88;70.23 58.41 100;86.54 94.18 42.71;100 86.42 65.56;56.99 43.62 33.36;47.82 13.7 91.13;51.16 49.51 72.49;78.01 20.32 54.99;77.56 95.34 30.01;40.13 86.58 96.24;30.47 68.45 77;65.33 23.26 100;23.5 64.2 66.65;69.82 74.73 78.22;56.27 43.34 100;51.4 60.57 76.66;58.4 40.38 57.31;70.8 44.75 37.83;16.74 41.15 49.49;64.67 92.57 20.01;94.7 18.52 100;56.77 88.08 87.28;31.47 50.66 100;20.89 64.01 47.89;100 79.56 61.32;32.57 22.67 51.53;32.5 100 48.4;54.37 62.26 39.42;39.53 97.78 70.21;70 94.58 39.06;27.89 91.27 79.93;88.28 41.02 100;98.63 22.79 58.41;92.33 35.52 91.67;34.83 87.87 33.58;47.76 55.69 100;58.04 13.86 27.48;99.44 100 25.44;36.12 33.34 100;29.71 61.6 81.66;78.16 98.9 94.38;93.26 34.1 56.92;26.55 18.53 90.25;42.48 28.47 48.35;43.8 79.31 43.33;68.09 15.79 100;90.97 61.66 76.4;100 25.59 66.35;45.8 100 52.92;43.77 76.24 82.21;55.13 100 99.42;23.56 92.87 23.49;77.2 54.38 63.61;96.39 29.34 78.64;31.03 83.35 100;15.79 32.85 88.08;100 25.03 39.93;100 57.67 65.78;23.78 71.09 98;46.1 68.02 26.4;38.1 50.01 29.85;81.87 64.83 100;91.75 44.66 48.72;39.76 81.26 82.2;80.37 85.26 23.38;79.19 84.73 65.7;94.59 87.39 56.04;66.52 97.69 54.79;31.49 93.21 96.87;58.84 44.37 36.4;57.17 29.27 100;92.77 49.97 93.56;48.84 100 25.06;54.06 100 100;96.56 60.54 30.16;69.82 55.17 94.21;49.09 34.71 100;55.15 56.85 33.39;52.57 61.57 100;61.76 76.09 53.27;32.08 98.75 47.84;67.22 63.39 59.62;85.4 100 97.2;95.78 22.69 86.62;29.25 14.34 100;100 27.94 81.41;78.63 19.78 55.47;50.82 32.34 53.68;17.95 100 88.61;100 78.85 27.05;100 57.17 38.85;69.56 56.43 100;57.47 89.86 30.74;19.56 19.9 71.17;93.87 14.94 75.74;20.83 31.41 73.11;89.1 36.98 98.58;69.72 23.91 100;63.47 32.34 100;100 50.02 100;55.78 56.09 63.75;82.1 37.95 84.63;45.04 30.77 77.84;64.51 26.94 38.59;85.45 29.61 54.84;42.44 66.84 23.5;44.67 61 98.86;34.2 16.08 74.35;64.54 88.19 25.62;40.63 100 38.82;38.21 30.89 46.58;100 89.22 100;25.03 24.71 66.16;36.66 28.9 26.06;97.15 11.94 96.18;93.05 70.95 100;17.83 53.75 71.09;35.69 81.08 39.27;71.7 36.42 37.68;36.77 15 85.27;55.84 81.37 75.4;71.71 25.53 61;46.42 32.61 38.98;16.9 41.57 70.62;100 65.94 92.19;64.43 58.27 100;41.02 68.92 36.33;41.98 55.83 46.39;22.18 30.05 40.63;26.29 69.13 97.36;50.51 15.81 83.23;91.33 40.64 22.76;88.03 49.65 100;62.96 12.12 62.72;16.28 13.06 83.82;100 47.07 100;40.73 90.17 66.94;22.91 42.16 64.57;100 80.64 55.53;44.47 77.03 74.55;70.21 99.22 99.95;26.52 82.89 77.11;100 43.74 38;53.11 18.68 85.8;77.3 35.05 53.94;17.44 100 100;91.6 32.16 100;97.24 35.02 100;50.26 41.96 100;41.99 100 84.49;69.24 44.6 100;71.34 60.83 29;50.76 10.64 56.53;91.85 22.6 30.16;49.06 20.92 100] (a) Use the colon operator to extract the marks from C03, and then find the average of those marks (using the 'sum' and 'length' commands). (b) Use vertical concatenation to create a single column vector consisting of all of the marks from all 3 sections. Then find the overall class average. Problem #3: Suppose that A is a 10 10 matrix, and we want to extract a submatrix consisting of rows 5 to 9, and columns 4 to 8 of A. What single Matlab command (using 10 characters or less) could accomplish this? (Assume that the matrix A has already been defined in Matlab, and has been called A.) Problem #3: Note that for this question you should test your answer to see if it works. For this purpose it would be useful to have a 10 x 10 matrix sitting around somewhere. There are several ways to quickly generate matrices in Matlab. For example, rand(10) will produce a 10 10 matrix whose entries are random numbers between 0 and 1. magic (10) will produce a 10 10 magic square matrix. Problem #4: Just Save Submit Problem #3 for Grading Problem #3 Attempt #1 Your Answer: Your Mark: Attempt #2 Problem #4: Open up your 'my_script.m' file that you created while working through Tutorial 2. Then copy and paste the 9 commands from the curve fitting example in Section 2.2 into your script file (you can delete any other commands that are in the file). Then save and execute your script file and make sure that the output produced (including the graph) agrees with the ouptut in the tutorial file. You should not proceed with the below question until this has been done correctly. Attempt #3 By modifying the appropriate lines in your script file, find the values of a, b, c, and d so that the cubic polynomial y = ax + bx + cx + d passes through the (x, y) pairs (-3, 2), (-2, 5), (-1, -2), and (0, 3). Just Save Note that to check your answer you can plot the given points together with your cubic polynomial on the same graph, and check to see that all 4 points lie on the curve (as in the tutorial file). Note that you will likely have to modify the t vector so that it corresponds with the range of x-values above. separate your answers with a comma Submit Problem #4 for Grading Problem #5: Find the values of a, b, c, and d so that the cubic polynomial y = ax + bx + cx + d provides the best fit to the following (x, y) pairs in the least squares sense: (-4, -10), (-3, 2), (-2, 5), (-1, -2), (0, 3), (1, 12). Problem #5: Note that to check your answer you can plot the given points together with your cubic polynomial on the same graph, and check to see that all 6 points lie fairly close to the curve (as in the tutorial file). But note that the curve might not pass directly through any of the 6 points. Just Save separate your answers with a comma Submit Problem #5 for Grading Problem #6: Consider the below vector x, which you can copy and paste directly into Matlab. The vector contains the final grades for each student in a large linear algebra course. Problem #6(a): Problem #6(b): x = [44 55 33 40 59 48 80 66 80 45 66 50 54 76 62 62 53 75 56 71 67 38 80 76 70 52 75 68 61 61 69 66 77 56 66 57 53 58 76 67 51 46 39 67 65 75 63 70 75 60 80 56 49 68 76 71 68 59 61 69 57 68 79 56 75 84 66 68 75 79 63 60 81 61 52 74 28 49 41 74 47 84 63 65 66 77 57 63 76 47 63 59 64 51 62 56 68 60 63 64 77 52 55 72 38 67 61 65 60 81 90 49 54 65 58 64 54 59 66 54 67 49 67 71 74 67 36 71 79 55 75 65 83 58 66 69 67 69 80 49 81 79 37 65 94 69 55 77 56 52 65 46 52 90 64 54 72 69 60 63 70 60 66 61 53 44 70 70 41 61 60 55 70 48 69 47 67 78 63 68 49 47 57 76 76 55 69 92 86 75 56 71 54 65 37 55 50 60 46 84 51 62 79 70 65 57 46 73 64 64 35 63 66 77 71 74 58 56 61 59 55 72 57 68 52 59 50 82 67 66 65 75 64 59 77 79 88 56 55 54 60 57 72 42 63 62 58 49 86 72 69 71 59 40 77 64 80 62 61 73 48 71 46 64 67 59 60 83 65 74 56 63 55 57 65 55 46 50 61 67 71 69 54 69 56 57 71 59 74 50 48 69 73 46 79 61 68 54 74 58 56 66 53 64 56 94 67 58 67 51 66 76 63 69 67 69 69 57 44 53 79 84 80 72 39 62 82 79 70 72 56 62 70 71 49 65 56 63 83 45 62 58 67 58 65 47 71 70 83 63 60 77 89 70 77 61 66 72 63 78 64 75 56 55 55 29 57 64 72 58 56 50 59 71 57 81 85 64 62 68 48 58 47 62 56 48 67 79 66 57 76 45 69 58 62 60 79 62 54 43 53 55 88 81 61 70 69 67 45 50 73 53 57 71 56 65 48 79 61 63 54 54 68 52 68 41 87 88 60 51 70 71 58 61 76 58 63 53 65 70 52 78 72 56 81 58 66 47 58 51 66 54 75 54 78 60 73 72 51 28 60 70 64 75 65 84 59 52 53 58 54 55 68 59 63 46 71 55 70 74 53 45 61 47 57 73 82 58 79 79 71 67 73 72 68 50 64 70 81 47 69 46 68 86 64 56 60 66 78 60 65 76 62 61 71 60 73 63 66 59 68 57 74 64 75 65 65 63 48 61 64 73 73 67 49 58 62 71 47 67 59 56 81 57 54 73 60 41 63 66 70 54 61 59 70 61 55 75 51 57 68 75 74 58 44 63 46 70 62 68 47 64 63 55 68 64 68 48 48 64 61 53 71 63 68 56 86 78 63 79 70 60 84 66 54 78 63 50 62 57 64 66 38 71 68 82 62 50 67 56 70 52 70 39 35 67 57 73 50 57 64 66 64 54 69 56 71 70 62 76 79 57 89 46 60 59 56 53 78 69 57 59 77 66 66 61 59 51 67 52 52 56 58 59 63 42 62 71 78 57 69 67 50 61 50 83 56 88 57 42 48 74 43 43 57 75 74 54 75 56 63 71 66 61 67 75 62 69 76 63 64 81 71 66 67 63 65 62 72 76 52 73 70 50 69 81 43 62 66 49 72 73 59 65 52 70 54 60 68 79 64 64 47 58 65 54 69 60 78 77 71 54 45 53 50 68 69 77 81 77 69 83 70 48 50 46 59 48 57 70 64 58 58 69 70 66 65 43 45 56 67 58 84 70 65 78 70 57 88 51 56 76 66 81 54 56 78 56 77 45 64 64 75 60 41 56 47 52 61 65 53 65 79 57 75 65 77 64 62 66 65 81 70 71 71 69 65 71 65 66 60 56 51 57 55 57 72 54 73 54 61 77 68 55 87 81 66 54 52 93 71 67 46 67 68 62 72 82 71 75 79 52 84 50 64 64 49 50 64 63 58 55 56 75 79 68 66 61 56 51 74 89 85 72 64 53 54 56 57 57 57 71 54 91 83 65 64 54 61 53 58 66 76 65 42 66 54 53 62 67 73 82 56 53 64 63 58 55 57 74 86 77 74 79 49 69 48 68 87 77 53 44 66 57 61 62 42 77 66 49 67 98 75 42 63 55 67 83 92 66 52 80 67 85 59 67 78 59 62 58 62 62 57 59 69 56 90 64 56 54 78 70 54 60 87 64 48 65 69 76 93 77 46 64 78 68 68 56 64 69 63 64 66 63 39 52 52 54 77 83 58 38 73 88 76 82 45 81 62 70 83 66 46 63 79 45 70 50 52 72 62 66 69 54 62 61 61 75 66 54 61 66 84 60 33 59 62 72 73 73 68 53 49 54 71 83 62 78]' (a) What proportion of students failed the course (i.e., got a mark of less than 50)? (Note that since the answer is a proportion, it must be between 0 and 1.) (b) What proportion of students got a B-, B, or B+ (i.e., got a mark between 70 and 79, inclusive)? Problem #7: Suppose that x is a vector and we want to raise every component of the vector x to the power 4, and we want to know how long Matlab took to perform this calculation. What Matlab commands (using 12 characters or less) could achieve this? Problem #7: Just Save Note that your answer must produce the desired result when copied and pasted directly into Matlab (assuming that the vector x has already been defined) Submit Problem #7 for Grading