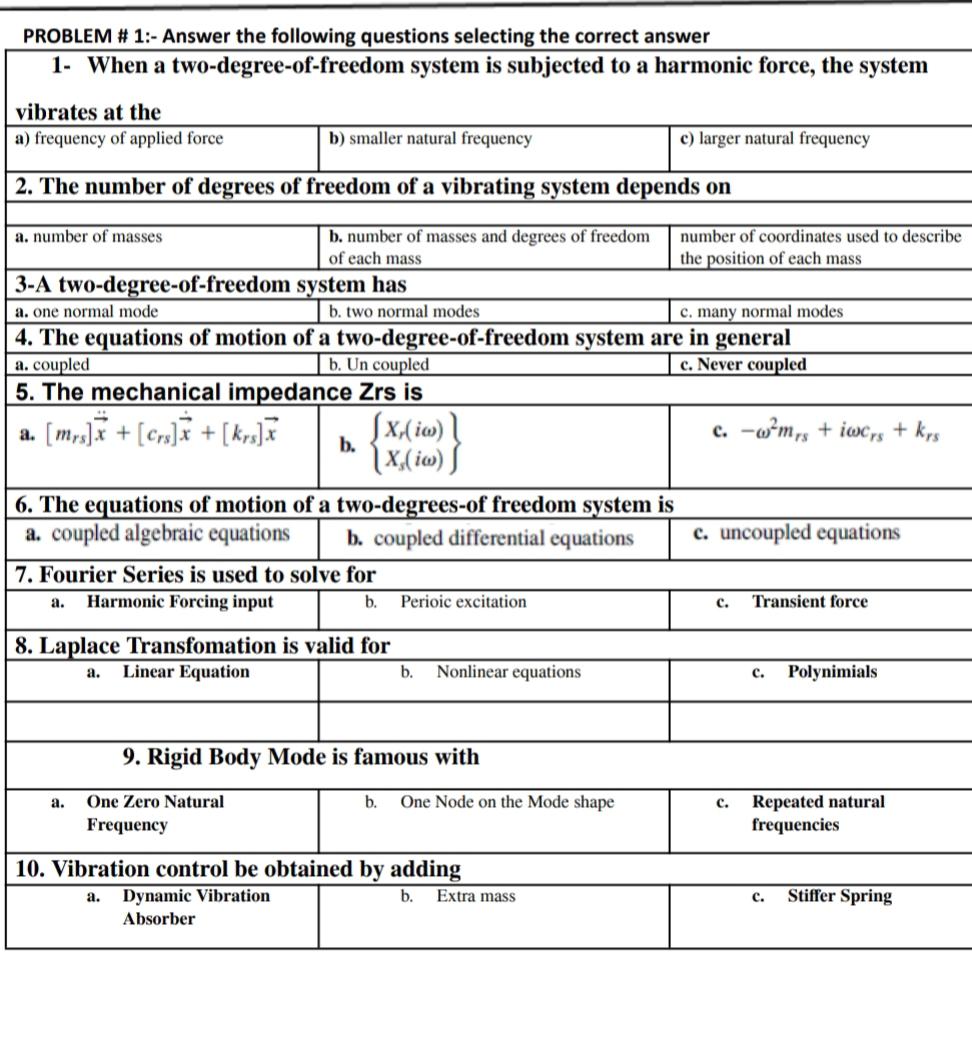
PROBLEM #1:- Answer the following questions selecting the correct answer 1- When a two-degree-of-freedom system is subjected to a harmonic force, the system vibrates at the a) frequency of applied force b) smaller natural frequency c) larger natural frequency 2. The number of degrees of freedom of a vibrating system depends on a. number of masses 3-A two-degree-of-freedom system has a. one normal mode b. number of masses and degrees of freedom of each mass number of coordinates used to describe. the position of each mass b. two normal modes b. Un coupled c. Never coupled c. many normal modes 4. The equations of motion of a two-degree-of-freedom system are in general a. coupled 5. The mechanical impedance Zrs is a. [mrs].x + [Crs] x + [ks]x b. [X, (io)\ [X, (io)] b. coupled differential equations 6. The equations of motion of a two-degrees-of freedom system is a. coupled algebraic equations 7. Fourier Series is used to solve for a. Harmonic Forcing input b. Perioic excitation 8. Laplace Transfomation is valid for c. -wmsiwers + krs c. uncoupled equations c. Transient force a. Linear Equation b. Nonlinear equations 9. Rigid Body Mode is famous with a. One Zero Natural Frequency b. One Node on the Mode shape c. 10. Vibration control be obtained by adding a. Dynamic Vibration Absorber b. Extra mass C. Polynimials Repeated natural frequencies C. Stiffer Spring