Problem 1 | Arithmetic in the AES MixColumns operation (22 marks) Recall that the MixColumns operation in AES performs arithmetic on 4-byte vectors using the polynomial M(y) = y⁴ + 1. In this arithmetic, we have M(y) = 0, so y⁴ = 1. (b) Next, we consider arithmetic involving the coeffcients of the polynomial c(y) = (03)y³ + (01)y² + (01)y + (02) ; that appears in MixColumns, where the coeffcients of c(y) are bytes written in hexadeci- mal (i.e. base 16) notation. Arithmetic involving this polynomial requires the computation of products involving the bytes (01), (02) and (03) in the Rijndahl field GF(2⁸). Recall that in this field, arithmetic is done modulo m(x) = x⁸ + x⁴ + x³ + x + 1. i. Write the bytes (01), (02), (03) as their respective polynomial representatives c₁(x), c₂(x) and c₃(x) in the Rijndahl field GF(2⁸). ii. (4 marks) Let b = (b₇ b₆ ... b₁ b₀) be any byte, and let d = (02)b be the product of the bytes (02) and b in the Rijndahl eld GF(2⁸). Then d is again a byte of the form d = (d₇ d₆ ... d₁ d₀). Provide symbolic expressions for the bits d_i, 0 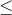i 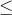7, in terms of the bits b_i of b. iii. Provide analogous expressions as in part (b) (ii) for the byte product e = (03)b, where b = (b₇ b₆ ... b₁ b₀) is any byte.

Transcribed image text