Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Problem 1 - One sample hypothesis test for mean of normal distribution (known standard deviation) A physical therapist wished to test the mean maximal



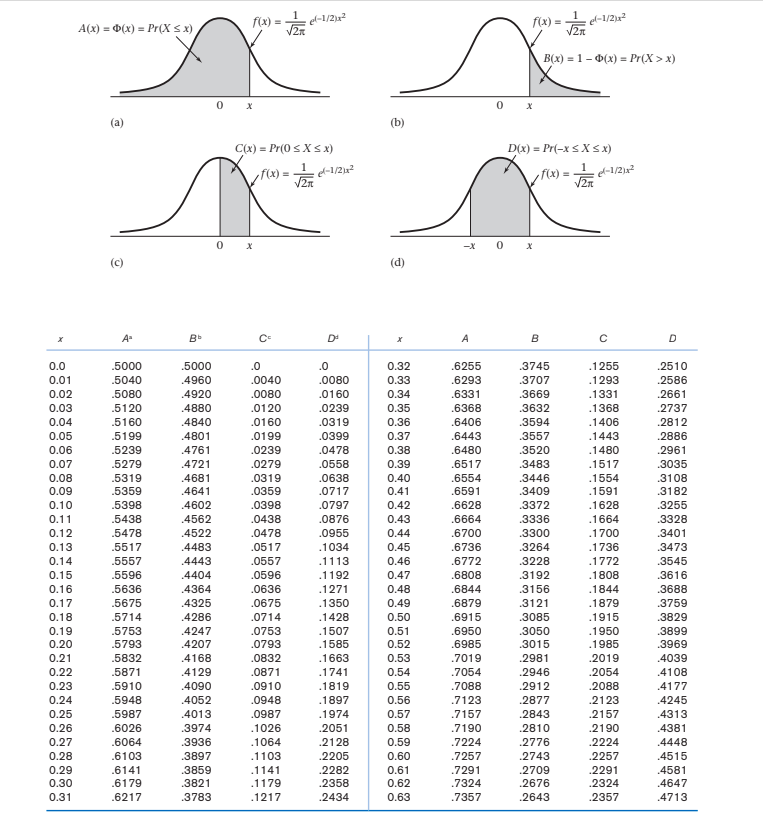

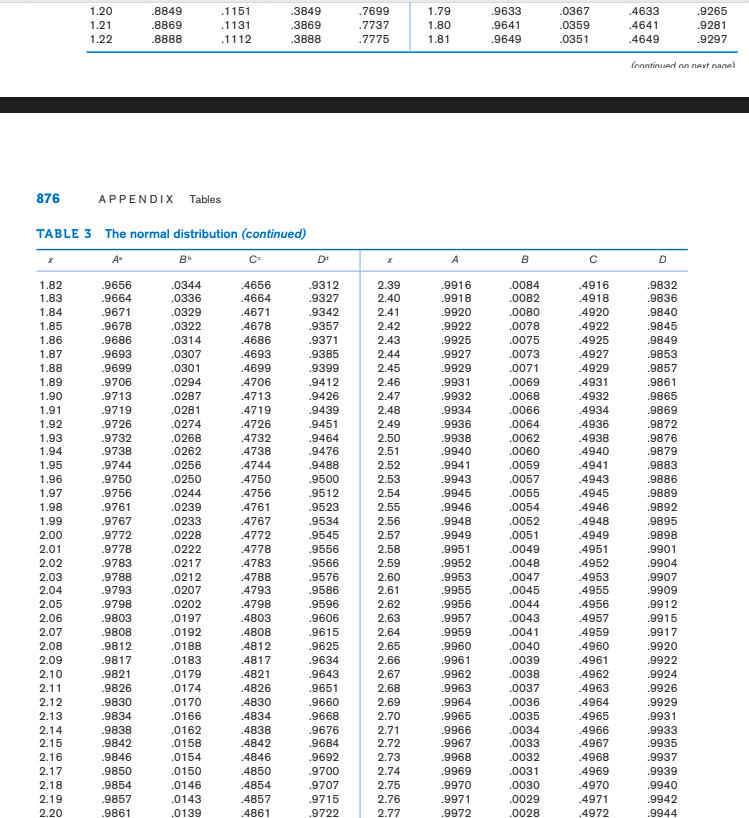
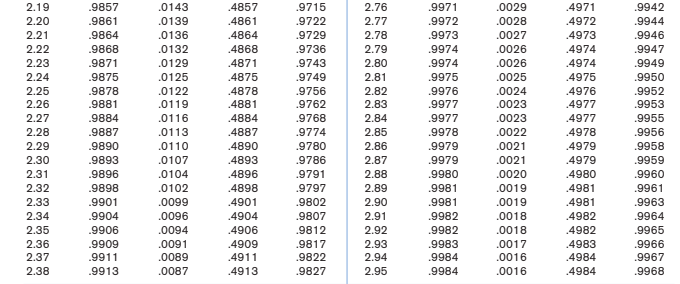
Problem 1 - One sample hypothesis test for mean of normal distribution (known standard deviation) A physical therapist wished to test the mean maximal strength of a particular muscle in a certain group. He is willing to assume that maximal strength scores are approximately normally distributed with a variance of 144. A sample of 15 subjects who participated in the experiment yielded a mean of 84.3. a) Do these data provide significant evidence, at 5% significance level, that the mean maximal strength is greater than 90? i. Write the null hypothesis (Ho) and alternative hypothesis (H1) of the test. Ho: = 90 vs. H:>90 (one-sided hypothesis test of the mean) ii. Determine the cut off for rejection region and the p-value and compare the conclusions. GIVEN: = 90; n = 15; x = 84.3; = = 144 = 12; = 0.05 known - therefore we calculate z-statistic for the hypothesis test of the mean. x-Ho 84.3-90 = -1.839667 z= 12 15 The cut off for rejection region for x> , or the critical value is Z0.05 = 1.645 Since -1.8397 -1.84) = P(Z < 1.84) = 0.9671 Since 0.9671> 00.5, we fail to reject Ho. Conclusion: Therefore, the experimental mean maximal muscle strength is not significantly greater than 90 at the a=0.05 significance level (z = -1.84, p = 0.967). In R, you can get the p-value using R code: pnorm(1.839667) b) Do these data provide significant evidence, at 5% significance level, that the mean maximal strength is less than 90? i. Write the null hypothesis (Ho) and alternative hypothesis (H1) of the test. Ho: = 90 vs. H1: |1.84]) = 2 * P(Z > 1.84) = 2 * 0.0329 = 0.0658 Since 0.0658 > 0.05, we fail to reject Ho Conclusion: Therefore, the experimental mean maximal muscle strength is not significantly different from 90 at the a=0.05 significance level. A(x)=(x) = P(X x) f(x)= (-1/2)x2 (a) 0 x C(x) = Pr(0 xx) f(x)= (-1/2)x 0 x f(x)= (-1/2) B(x)=1(x) = Pr(X>x) X D(x) = Pr(-x xx) 0 x -x 0 x (c) (d) f(x) = (-1/2)x2 x A Bb C Dd x A B C D 0.0 .5000 .5000 .0 .0 0.32 .6255 .3745 .1255 .2510 0.01 .5040 .4960 .0040 .0080 0.33 .6293 .3707 .1293 .2586 0.02 .5080 .4920 .0080 .0160 0.34 .6331 .3669 .1331 .2661 0.03 .5120 .4880 .0120 .0239 0.35 .6368 .3632 .1368 .2737 0.04 .5160 .4840 .0160 .0319 0.36 .6406 .3594 .1406 .2812 0.05 .5199 .4801 .0199 .0399 0.37 .6443 .3557 .1443 .2886 0.06 .5239 .4761 .0239 .0478 0.38 .6480 .3520 .1480 .2961 0.07 .5279 .4721 .0279 .0558 0.39 .6517 .3483 .1517 .3035 0.08 .5319 .4681 .0319 .0638 0.40 .6554 .3446 .1554 .3108 0.09 .5359 .4641 .0359 .0717 0.41 .6591 .3409 .1591 .3182 0.10 .5398 .4602 .0398 .0797 0.42 .6628 .3372 .1628 .3255 0.11 .5438 .4562 .0438 .0876 0.43 .6664 .3336 .1664 .3328 0.12 .5478 .4522 .0478 .0955 0.44 .6700 .3300 .1700 .3401 0.13 .5517 .4483 .0517 .1034 0.45 .6736 .3264 .1736 .3473 0.14 .5557 .4443 .0557 .1113 0.46 .6772 .3228 .1772 .3545 0.15 .5596 .4404 .0596 .1192 0.47 .6808 .3192 .1808 .3616 0.16 .5636 .4364 .0636 .1271 0.48 .6844 .3156 .1844 .3688 0.17 .5675 .4325 .0675 .1350 0.49 .6879 .3121 .1879 .3759 0.18 .5714 .4286 .0714 .1428 0.50 .6915 .3085 .1915 .3829 0.19 .5753 .4247 .0753 .1507 0.51 .6950 .3050 .1950 .3899 0.20 .5793 .4207 .0793 .1585 0.52 .6985 .3015 .1985 .3969 0.21 .5832 .4168 .0832 .1663 0.53 .7019 .2981 .2019 .4039 0.22 .5871 .4129 .0871 .1741 0.54 .7054 .2946 .2054 .4108 0.23 .5910 .4090 .0910 .1819 0.55 .7088 .2912 .2088 .4177 0.24 .5948 .4052 .0948 .1897 0.56 .7123 .2877 .2123 .4245 0.25 .5987 .4013 .0987 .1974 0.57 .7157 .2843 .2157 .4313 0.26 .6026 .3974 .1026 .2051 0.58 .7190 .2810 .2190 .4381 0.27 .6064 .3936 .1064 .2128 0.59 .7224 .2776 .2224 .4448 0.28 .6103 .3897 .1103 .2205 0.60 .7257 .2743 .2257 .4515 0.29 .6141 .3859 .1141 .2282 0.61 .7291 .2709 .2291 .4581 0.30 .6179 .3821 .1179 .2358 0.62 .7324 .2676 .2324 .4647 0.31 .6217 .3783 .1217 .2434 0.63 .7357 .2643 .2357 .4713 A Bb C Dd A B D 0.64 .7389 2611 .2389 .4778 1.23 .8907 .1093 .3907 .7813 0.65 .7422 .2578 .2422 .4843 1.24 .8925 .1075 .3925 .7850 0.66 .7454 .2546 .2454 .4907 1.25 .8944 .1056 .3944 .7887 0.67 .7486 .2514 .2486 .4971 1.26 .8962 .1038 .3962 .7923 0.68 .7517 .2483 .2517 .5035 1.27 .8980 .1020 .3980 .7959 0.69 .7549 .2451 .2549 .5098 1.28 .8997 .1003 .3997 .7995 0.70 .7580 .2420 .2580 .5161 1.29 .9015 .0985 .4015 .8029 0.71 .7611 .2389 .2611 .5223 1.30 .9032 .0968 .4032 .8064 0.72 .7642 .2358 .2642 .5285 1.31 .9049 .0951 .4049 .8098 0.73 .7673 .2327 .2673 .5346 1.32 .9066 .0934 .4066 .8132 0.74 .7703 .2297 .2703 .5407 1.33 .9082 .0918 .4082 .8165 0.75 .7734 .2266 .2734 .5467 1.34 .9099 .0901 .4099 .8198 0.76 .7764 .2236 .2764 .5527 1.35 .9115 .0885 .4115 .8230 0.77 .7793 .2207 .2793 .5587 1.36 .9131 .0869 .4131 .8262 0.78 .7823 .2177 .2823 .5646 1.37 .9147 .0853 .4147 .8293 0.79 .7852 .2148 .2852 .5705 1.38 .9162 .0838 .4162 .8324 0.80 .7881 .2119 .2881 .5763 1.39 .9177 .0823 .4177 .8355 0.81 .7910 .2090 .2910 .5821 1.40 .9192 .0808 .4192 .8385 0.82 .7939 .2061 .2939 .5878 1.41 .9207 .0793 .4207 .8415 0.83 .7967 .2033 .2967 .5935 1.42 .9222 .0778 .4222 .8444 0.84 .7995 .2005 .2995 .5991 1.43 .9236 .0764 .4236 .8473 0.85 .8023 .1977 .3023 .6047 1.44 .9251 .0749 .4251 .8501 0.86 .8051 .1949 .3051 .6102 1.45 .9265 .0735 .4265 .8529 0.87 .8078 .1922 .3078 .6157 1.46 .9279 .0721 .4279 .8557 0.88 .8106 .1894 .3106 .6211 1.47 .9292 .0708 .4292 .8584 0.89 .8133 .1867 .3133 .6265 1.48 .9306 .0694 .4306 .8611 0.90 .8159 .1841 .3159 .6319 1.49 .9319 .0681 .4319 .8638 0.91 .8186 .1814 .3186 .6372 1.50 .9332 .0668 .4332 .8664 0.92 .8212 .1788 .3212 .6424 1.51 .9345 .0655 .4345 .8690 0.93 .8238 .1762 .3238 .6476 1.52 .9357 .0643 .4357 .8715 0.94 .8264 .1736 .3264 .6528 1.53 .9370 .0630 .4370 .8740 0.95 .8289 .1711 .3289 .6579 1.54 .9382 .0618 .4382 .8764 0.96 .8315 .1685 .3315 .6629 1.55 .9394 .0606 .4394 .8789 0.97 .8340 .1660 .3340 .6680 1.56 .9406 .0594 .4406 .8812 0.98 .8365 .1635 .3365 .6729 1.57 .9418 .0582 .4418 .8836 0.99 .8389 .1611 .3389 .6778 1.58 .9429 .0571 .4429 .8859 1.00 .8413 .1587 .3413 .6827 1.59 .9441 .0559 .4441 .8882 1.01 .8438 .1562 .3438 .6875 1.60 .9452 .0548 .4452 .8904 1.02 .8461 .1539 .3461 .6923 1.61 .9463 .0537 .4463 .8926 1.03 .8485 .1515 .3485 .6970 1.62 .9474 .0526 .4474 .8948 1.04 .8508 .1492 .3508 .7017 1.63 .9484 .0516 .4484 .8969 1.05 .8531 .1469 .3531 .7063 1.64 .9495 .0505 .4495 .8990 1.06 .8554 .1446 .3554 .7109 1.65 .9505 .0495 .4505 .9011 1.07 .8577 .1423 .3577 .7154 1.66 .9515 .0485 .4515 .9031 1.08 .8599 .1401 .3599 .7199 1.67 .9525 .0475 .4525 .9051 1.09 .8621 .1379 .3621 .7243 1.68 .9535 .0465 .4535 .9070 1.10 .8643 .1357 .3643 .7287 1.69 .9545 .0455 .4545 .9090 1.11 .8665 .1335 .3665 .7330 1.70 .9554 .0446 .4554 .9109 1.12 .8686 .1314 .3686 .7373 1.71 .9564 .0436 .4564 .9127 1.13 .8708 .1292 .3708 .7415 1.72 .9573 .0427 .4573 .9146 1.14 .8729 .1271 .3729 .7457 1.73 .9582 .0418 .4582 .9164 1.15 .8749 .1251 .3749 .7499 1.74 .9591 .0409 .4591 .9181 1.16 .8770 .1230 .3770 .7540 1.75 .9599 .0401 .4599 .9199 1.17 .8790 .1210 .3790 .7580 1.76 .9608 .0392 .4608 .9216 1.18 .8810 .1190 .3810 .7620 1.77 .9616 .0384 .4616 .9233 1.19 .8830 .1170 .3830 .7660 1.78 .9625 .0375 .4625 .9249 1.20 .8849 .1151 3849 7699 1.79 9633 .0367 4633 9265 1.20 .8849 .1151 .3849 .7699 1.79 .9633 .0367 .4633 .9265 1.21 .8869 .1131 .3869 .7737 1.80 .9641 .0359 .4641 .9281 1.22 .8888 .1112 .3888 .7775 1.81 .9649 .0351 .4649 .9297 876 APPENDIX Tables TABLE 3 The normal distribution (continued) (continued on next name) x A Bb C Dd x A B C D 1.82 .9656 .0344 .4656 .9312 2.39 .9916 .0084 .4916 .9832 1.83 .9664 .0336 .4664 .9327 2.40 .9918 .0082 .4918 .9836 1.84 .9671 .0329 .4671 .9342 2.41 .9920 .0080 .4920 .9840 1.85 .9678 .0322 .4678 .9357 2.42 .9922 .0078 .4922 .9845 1.86 .9686 .0314 .4686 .9371 2.43 .9925 .0075 .4925 .9849 1.87 .9693 .0307 .4693 .9385 2.44 .9927 .0073 .4927 .9853 1.88 .9699 .0301 .4699 .9399 2.45 .9929 .0071 .4929 .9857 1.89 .9706 .0294 .4706 .9412 2.46 .9931 .0069 .4931 .9861 1.90 .9713 .0287 .4713 .9426 2.47 .9932 .0068 .4932 .9865 1.91 .9719 .0281 .4719 .9439 2.48 .9934 .0066 .4934 .9869 1.92 .9726 .0274 .4726 .9451 2.49 .9936 .0064 .4936 .9872 1.93 .9732 .0268 .4732 .9464 2.50 .9938 .0062 .4938 .9876 1.94 .9738 .0262 .4738 .9476 2.51 .9940 .0060 .4940 .9879 1.95 .9744 .0256 .4744 .9488 2.52 .9941 .0059 .4941 .9883 1.96 .9750 .0250 .4750 .9500 2.53 .9943 .0057 .4943 .9886 1.97 .9756 .0244 .4756 .9512 2.54 .9945 .0055 .4945 .9889 1.98 .9761 .0239 .4761 .9523 2.55 .9946 .0054 .4946 .9892 1.99 .9767 .0233 .4767 .9534 2.56 .9948 .0052 .4948 .9895 2.00 .9772 .0228 .4772 .9545 2.57 .9949 .0051 .4949 .9898 2.01 .9778 .0222 .4778 .9556 2.58 .9951 .0049 .4951 .9901 2.02 .9783 .0217 .4783 .9566 2.59 .9952 .0048 .4952 .9904 2.03 .9788 .0212 .4788 .9576 2.60 .9953 .0047 .4953 .9907 2.04 .9793 .0207 .4793 .9586 2.61 .9955 .0045 .4955 .9909 2.05 .9798 .0202 .4798 .9596 2.62 .9956 .0044 .4956 .9912 2.06 .9803 .0197 .4803 .9606 2.63 .9957 .0043 .4957 .9915 2.07 .9808 .0192 .4808 .9615 2.64 .9959 .0041 .4959 .9917 2.08 .9812 .0188 .4812 .9625 2.65 .9960 .0040 .4960 .9920 2.09 .9817 .0183 .4817 .9634 2.66 .9961 .0039 .4961 .9922 2.10 .9821 .0179 .4821 .9643 2.67 .9962 .0038 .4962 .9924 2.11 .9826 .0174 .4826 .9651 2.68 .9963 .0037 .4963 .9926 2.12 .9830 .0170 .4830 .9660 2.69 .9964 .0036 .4964 .9929 2.13 .9834 .0166 .4834 .9668 2.70 .9965 .0035 .4965 .9931 2.14 .9838 .0162 .4838 .9676 2.71 .9966 .0034 .4966 .9933 2.15 .9842 .0158 .4842 .9684 2.72 .9967 .0033 .4967 .9935 2.16 .9846 .0154 .4846 .9692 2.73 .9968 .0032 .4968 .9937 2.17 .9850 .0150 .4850 .9700 2.74 .9969 .0031 .4969 .9939 2.18 .9854 .0146 .4854 .9707 2.75 .9970 .0030 .4970 .9940 2.19 .9857 .0143 .4857 .9715 2.76 .9971 .0029 .4971 .9942 2.20 .9861 .0139 .4861 .9722 2.77 .9972 .0028 .4972 .9944 2.19 .9857 .0143 .4857 .9715 2.76 .9971 .0029 .4971 .9942 2.20 .9861 .0139 .4861 .9722 2.77 .9972 .0028 .4972 .9944 2.21 .9864 .0136 .4864 .9729 2.78 .9973 .0027 .4973 .9946 2.22 .9868 .0132 .4868 .9736 2.79 .9974 .0026 .4974 .9947 2.23 .9871 .0129 .4871 .9743 2.80 .9974 .0026 .4974 .9949 2.24 .9875 .0125 .4875 .9749 2.81 .9975 .0025 .4975 .9950 2.25 .9878 .0122 .4878 .9756 2.82 .9976 .0024 .4976 .9952 2.26 .9881 .0119 .4881 .9762 2.83 .9977 .0023 .4977 .9953 2.27 .9884 .0116 .4884 .9768 2.84 .9977 .0023 .4977 .9955 2.28 .9887 .0113 .4887 .9774 2.85 .9978 .0022 .4978 .9956 2.29 .9890 .0110 .4890 .9780 2.86 .9979 .0021 .4979 .9958 2.30 .9893 .0107 .4893 .9786 2.87 .9979 .0021 .4979 .9959 2.31 .9896 .0104 .4896 .9791 2.88 .9980 .0020 .4980 .9960 2.32 .9898 .0102 .4898 .9797 2.89 .9981 .0019 .4981 .9961 2.33 .9901 .0099 .4901 .9802 2.90 .9981 .0019 .4981 .9963 2.34 .9904 .0096 .4904 .9807 2.91 .9982 .0018 .4982 .9964 2.35 .9906 .0094 .4906 .9812 2.92 .9982 .0018 .4982 .9965 2.36 .9909 .0091 .4909 .9817 2.93 .9983 .0017 .4983 .9966 2.37 .9911 .0089 .4911 .9822 2.94 .9984 .0016 .4984 .9967 2.38 .9913 .0087 .4913 .9827 2.95 .9984 .0016 .4984 .9968
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


