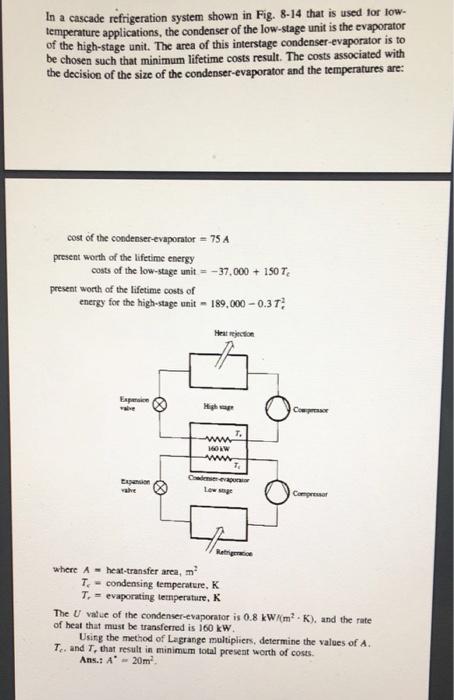
The flow rate of raw material to the processing plant shown in Fig. 7-7 is 10 kg/s of mixture consisting of 50 percent A and 50 percent B. The separator can remove some of material A in pure form, and this product has a selling price of $10 per kilogram. The other product from the separator sells for $2 per kilogram, and some of this stream may be recycled. The cost of operating the separator in dollars per second is where w mass rate of flow, kg/s 0.2w 1- (w/wx1) x = fraction of A in the mixture (This separator cost equation indicates that the cost becomes infinite for perfect separation.) (a) Set up the objective function in terms of w, w, and x to maximize the profit. The cost of the raw material is constant. Mixture of A and B x = 0.5, w = 10 kg/s WI.FI Separator 2 w.12= 1.0. pure A 3 w3.x3 WA.XA ws.xs Os (b) Set up the constraint(s) in terms of w, w, and x. Ans.: (b) (5-wx)(ww) = (10w)(wx1w). $10/kg $2/kg A desalination plant shown schematically in Fig. 7-11, receives sea water having a saline concentration by mass of 3% of the mixture. This sea water is mixed with some recycle solution and enters the plant which is to have a capacity of 300 kg/s. The cost of pumping and treating the raw sea water is Sea water 3% salt, Qkg/s Discharge Treatment facility x = % salt w = flow rate of mixture, kg/s Q Recycle R kg/s Desalination plant Fresh water 300 kg/s y=% salt $0.08 per Mg of mixture, and the cost of heat to operate the plant is $0.10 per Mg of feed. As the salt concentration entering the desalination plant increases, the effectiveness of the plant decreases, following the equation y = 3.4x, so should the entering concentration reach 11.56% the plant would produce no fresh water. Develop the objective function and constraint to describe the minimum-cost operation. Ans.: constraint is (300) (11.56) (w-300) 11.56(w300) - 3w F kg/s In a cascade refrigeration system shown in Fig. 8-14 that is used for low- temperature applications, the condenser of the low-stage unit is the evaporator of the high-stage unit. The area of this interstage condenser-evaporator is to be chosen such that minimum lifetime costs result. The costs associated with the decision of the size of the condenser-evaporator and the temperatures are: cost of the condenser-evaporator = 75 A present worth of the lifetime energy costs of the low-stage unit present worth of the lifetime costs of energy for the high-stage unit Expemaion valve Expansion valve -37,000+ 150 T 189,000-0.37 where A heat-transfer area, m Heat rejection High age www 1600 www Condenser evapursor Low soge T Refrigeration T-condensing temperature, K T.= evaporating temperature, K Compressor Compressor The U value of the condenser-evaporator is 0.8 kW/(m-K), and the rate of heat that must be transferred is 160 kW. Using the method of Lagrange multipliers, determine the values of A. T. and T, that result in minimum total present worth of costs. Ans.: A 20m. Problem 4 A solar collector and storage tank, shown in Fig. 8-15a. is to be optimized to achieve minimum first cost. During the day the temperature of water in the storage vessel is elevated from 25C (the minimum useful temperature) to Imax, as shown in Fig. 8-156. The collector receives 260 W/m of solar ener- gy, but there is heat loss from the collector to ambient air by convection. The convection coefficient is 2 W/(mK). and the average temperature differ- ence during the 10-hour day is (25+ max)/2 minus the ambient temperature of 10C. The energy above the minimum useful temperature of 25C that is to be stored in the vessel during the day is 200,000 kJ. The density of water is 1000 kg/m, and its specific heat is 4.19 kJ/(kg K). The cost of the solar collector in dollars is 20A, where A is the area in square meters, and the cost of the storage vessel in dollars is 101.5V, where V is the volume in cubic meters. (a) Using A and V as the variables. set up the objective function and constraint to optimize the first cost. (b) Develop the Lagrange multiplier equations and verify that they are satisfied by V 1.2 m and A = 29.2 m. - Ans.: (a) y = 20A + 101.5V, subject to A(230-47.7/V) = 5555. Storage tank Collector (a) Temperature, "C Imax 25C, lowest useful temperature 10C ambient Time (b) 10 h = 36,000 s