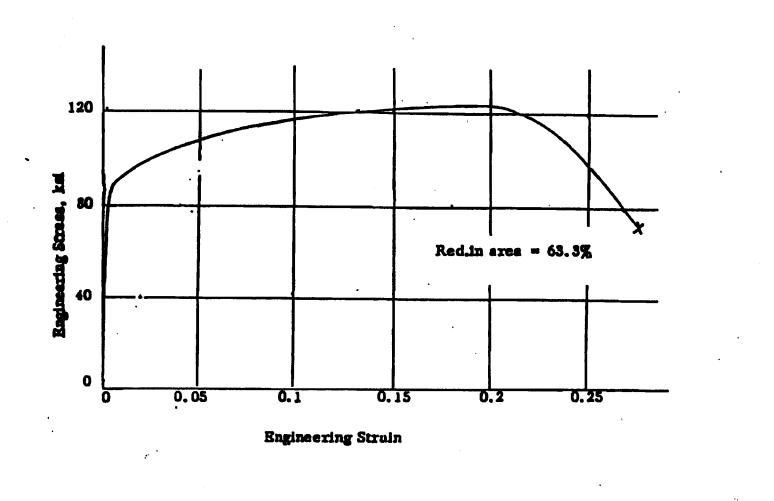
Two specimens of the same material and identical geometry are subjected to the following two deformation conditions: from zero deformation up to necking from zero deformation up to fracture (a) For each case, derive an expression for the total deformation work per unit volume (strain energy density) in terms of the elastic modulus E, yield strain y, strain hardening exponent m, strength coefficient K, true strain at fracture &, and true stress at fracture of. (b) Discuss the significance of each term in the previous two cases for the special cases of ductile and brittle material behaviors (use true stress and strain definitions). First specimen: Second specimen: Problem 2 Using the engineering stress-strain plot shown in the next page, determine the following assuming a reduction in cross-section area at fracture equal to 63.3%. (1) ultimate tensile strength (2) 0.2% offset yield strength (3) elastic modulus (4) true plastic strain at necking (5) true stress at necking (6) true fracture strength (7) true fracture strain (8) strength coefficient (9) elongation at fracture Engineering Stress, kal 120 80 40 0.05 0.1 0.15 Engineering Strain k Red.in area= 63.3% 0.2 0.25 Problem 3 A thin-walled cylinder of length L, radius R, and thickness is closed at both ends and pressurized internally with pressure p. The cylinder is made of an isotropic material of elastic modulus E, Poisson ratio v, and uniaxial yield strength 0. (a) Find the stresses at a radial distance r (i.e., point A) as a function of p, f, and r and then write them in the form of a 3 x 3 stress tensor . Obtain the tensor for the outside surface. (b) Determine the strain tensor & corresponding to point A in terms of p, R, t, E, and v and write them in the form of a 3 x 3 strain tensor &y. Obtain the tensor for the outside surface. (c) Obtain expressions for the change in length AL, change in thickness A, and change in circumference A(2R). (d) Using the von Mises equivalent stress, determine the pressure that will cause yielding. Note: For questions (b)-(d), you can disregard the effect of the stress in the z direction as negligibly small. Problem 4 A thin-walled cylindrical pressure vessel with closed ends is subjected to an internal pressure of 10 MPa. The mean diameter of the vessel is 1.0 m and the wall thickness is 0.01 m. The material is a steel alloy with elastic modulus E = 207 GPa, Poisson ratio v=0.3, and yield strength Sy = 800 MPa. (a) What is the maximum shear stress in the vessel? Sketch the plane and direction of the maximum shear stress in the wall showing clearly the axes (x = axis of cylinder, r = radial direction, >= tangential direction) in your sketch. (b) Using the von Mises yield criterion, determine the safety factor for yielding. (c) If the pressure is increased from 0 to 10 MPa, find the total radial displacement of the wall of the cylindrical section of the pressure vessel and the three stain invariants.