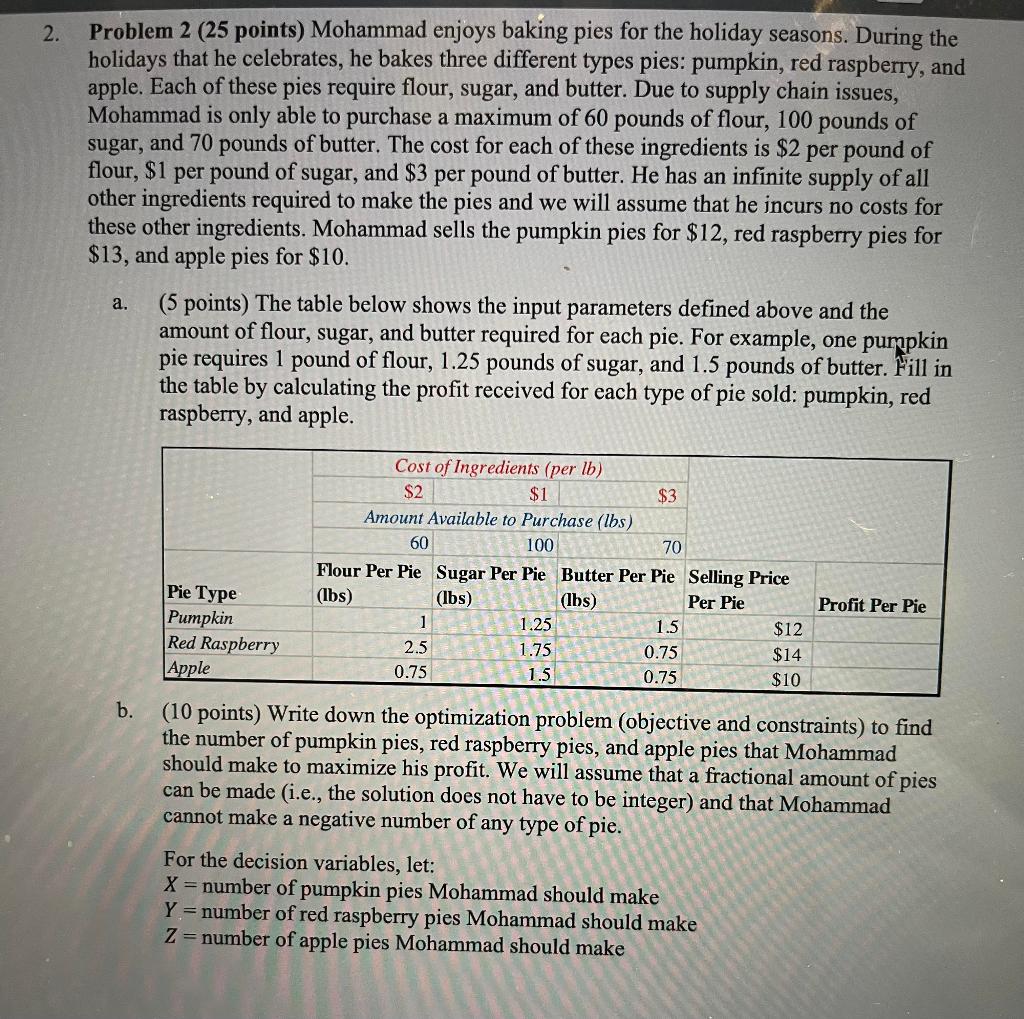
Problem 2 ( 25 points) Mohammad enjoys baking pies for the holiday seasons. During the holidays that he celebrates, he bakes three different types pies: pumpkin, red raspberry, and apple. Each of these pies require flour, sugar, and butter. Due to supply chain issues, Mohammad is only able to purchase a maximum of 60 pounds of flour, 100 pounds of sugar, and 70 pounds of butter. The cost for each of these ingredients is $2 per pound of flour, $1 per pound of sugar, and $3 per pound of butter. He has an infinite supply of all other ingredients required to make the pies and we will assume that he incurs no costs for these other ingredients. Mohammad sells the pumpkin pies for $12, red raspberry pies for $13, and apple pies for $10. a. (5 points) The table below shows the input parameters defined above and the amount of flour, sugar, and butter required for each pie. For example, one purpkin pie requires 1 pound of flour, 1.25 pounds of sugar, and 1.5 pounds of butter. Fill in the table by calculating the profit received for each type of pie sold: pumpkin, red raspberry, and apple. b. (10 points) Write down the optimization problem (objective and constraints) to find the number of pumpkin pies, red raspberry pies, and apple pies that Mohammad should make to maximize his profit. We will assume that a fractional amount of pies can be made (i.e., the solution does not have to be integer) and that Mohammad cannot make a negative number of any type of pie. For the decision variables, let: X= number of pumpkin pies Mohammad should make Y= number of red raspberry pies Mohammad should make Z= number of apple pies Mohammad should make c. (5 points) Solve the problem from part (b) using Excel or your optimization solver of choice. Clearly indicate the optimal value for X,Y, and Z and the corresponding objective value. If you get a fractional answer, round to the hundredths place. d. (5 points) In reality, Mohammad cannot make a fractional amount of pies. Use the values that you found in part (c) and round the production of each pie type to the nearest integer: i. (3 points) Is the optimization problem with the integer solution feasible (yes or no)? If you responded no, specify which constraint(s) are violated. ii. (2 points) What is the objective value of the (possibly infeasible) integer solution you obtain by rounding the fractional solution