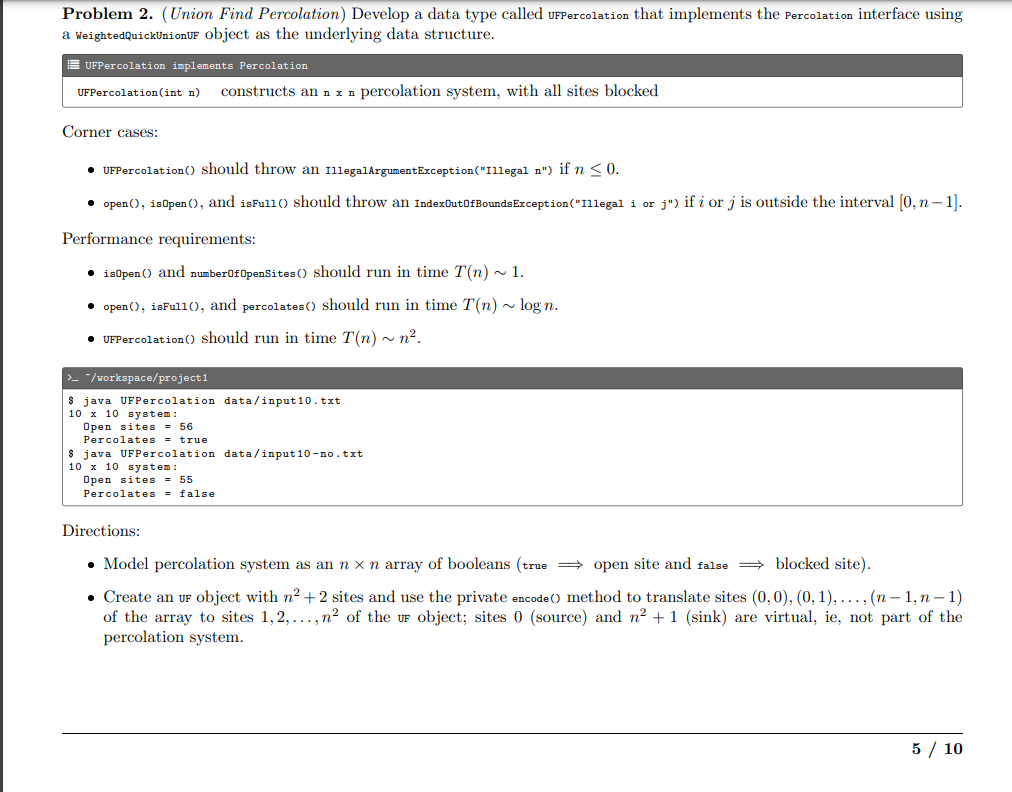
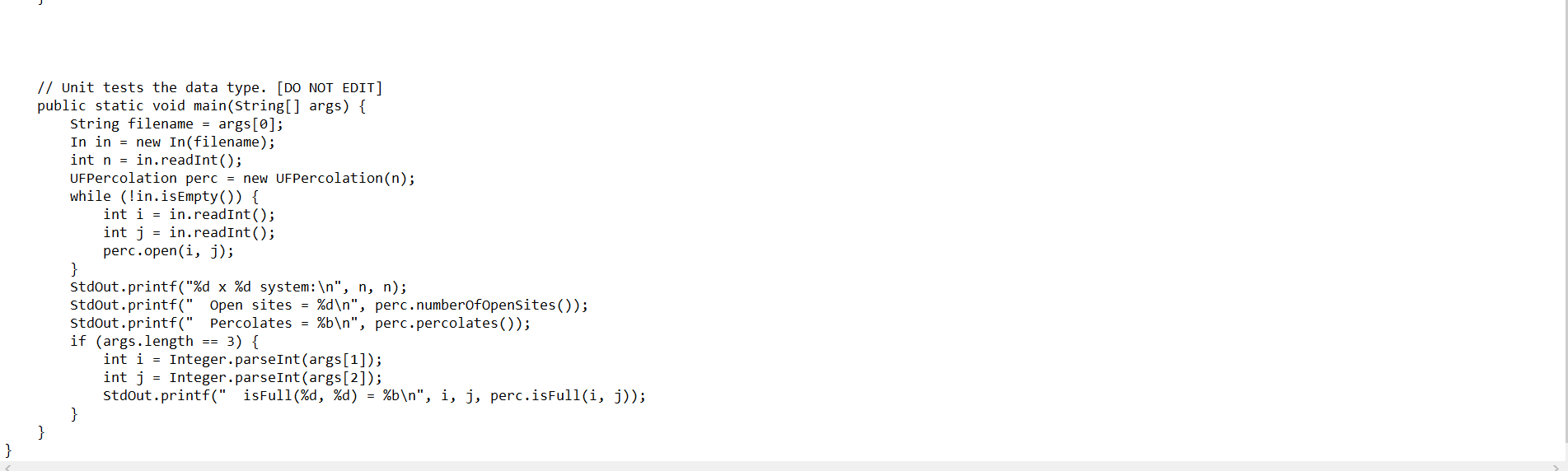
Problem 2. (Union Find Percolation) Develop a data type called UFPercolation that implements the Percolation interface using a WeightedQuickUnionUF object as the underlying data structure. UFPercolation implements Percolation UFPercolation(int n) constructs an n x n Corner cases: UFPercolation() should throw an IllegalArgumentException("Illegal n") if n 0. open(), isOpen(), and isFul1() should throw an IndexOutOfBounds Exception ("Illegal i or j") ifi or j is outside the interval [0, n-1]. Performance requirements: isOpen() and number0fOpenSites() should run in time T(n)~ 1. open(), isFull(), and percolates () should run in time T(n) ~ logn. UFPercolation() should run in time T(n) ~ n. > "/workspace/project1 $ java UFPercolation data/input10.txt 10 x 10 system: Open sites = 56 Percolates = true percolation system, with all sites blocked $ java UFPercolation data/input 10-no.txt 10 x 10 system: Open sites = 55 Percolates = false Directions: Model percolation system as an n x n array of booleans (true open site and false blocked site). Create an UF object with n+2 sites and use the private encode() method to translate sites (0,0), (0, 1),..., (n-1, n-1) of the array to sites 1, 2,..., n of the UF object; sites 0 (source) and n + 1 (sink) are virtual, ie, not part of the percolation system. 5 / 10 A 3 x 3 percolation system and its UF representation 0,0 0,1 0,2 1,0 1,1 1,2 2,0 2,1 2,2 Project 1 (Percolation) Instance variables: - Percolation system size, int n. - Percolation system, boolean [] [] open. - Number of open sites, int openSites. Union-find representation of the percolation system, WeightedQuickUnionUF uf. - Initialize instance variables. 1 4 7 0 2 8 10 private int encode(int i, int j) - Return the UF site (1,2,..., n) corresponding to the percolation system site (i, j). public UFPercolation (int n) 3 6 9 void open (int i, int j) - If site (i, j) is not open: * Open the site * Increment openSites by one. * If the site is in the first (or last) row, connect the corresponding uf site with the source (or sink). * If any of the neighbors to the north, east, west, and south of site (i, j) is open, connect the uf site corresponding to site (i, j) with the uf site corresponding to that neighbor. boolean isFull (int i, int j) Return whether site (i, j) is full or not a site is full if it is open and its corresponding uf site is connected to the source. int number Of OpenSites () - Return the number of open sites. boolean percolates () Return whether the system percolates or not a system percolates if the sink is connected to the source. Using virtual source and sink sites introduces what is called the back wash problem. 0,0 0,1 0,2 1,0 1,1 1,2 Project 1 (Percolation) In the 3 x 3 system, consider opening the sites (0,1), (1, 2), (1, 1), (2,0), and (2, 2), and in that order; the system percolates once (2, 2) is opened. 2,0 2,1 2,2 1 4 7 0 2 5 8 10 3 6 6 / 10 9 The site (2, 0) is technically not full since it is not connected to an open site in the top row via a path of neighboring (north, east, west, and south) open sites, but the corresponding uf site (7) is connected to the source, so is incorrectly reported as being full this is the back wash problem. To receive full credit, you must resolve the back wash problem. UFPercolation - Notepad File Edit Format View Help import dsa.WeightedQuickUnionUF; import stdlib.In; import stdlib.stdout; // An implementation of the Percolation API using the UF data structure. public class UFPercolation implements Percolation { // Constructs an n x n percolation system, with all sites blocked. public UFPercolation (int n) { } // Opens site (i, j) if it is not already open. public void open(int i, int j) { } // Returns true if site (i, j) is open, and false otherwise. public boolean isOpen(int i, int j) { } // Returns true if site (i, j) is full, and false otherwise. public boolean isFull(int i, int j) { } // Returns the number of open sites. public int numberOfOpenSites () { } // Returns true if this system percolates, and false otherwise. public boolean percolates () { } // Returns an integer ID (1...n) for site (i, j). private int encode(int i, int j) { } I X } // Unit tests the data type. [DO NOT EDIT] public static void main(String[] args) { String filename = args [0]; In in new In (filename); int n = in.readInt (); UFPercolation perc = new UFPercolation (n); while (!in.isEmpty()) { } } int i in.readInt (); int j = in.readInt (); perc.open(i, j); stdout.printf("%d x %d system: ", n, n); stdout.printf(" Open sites = %d ", perc.numberOfOpenSites ()); stdout.printf(" Percolates = %b ", perc.percolates()); if (args.length == 3) { int i = Integer.parseInt(args[1]); int j = Integer.parseInt (args[2]); stdout.printf(" is Full (%d, %d) = %b ", i, j, perc.isFull(i, j));