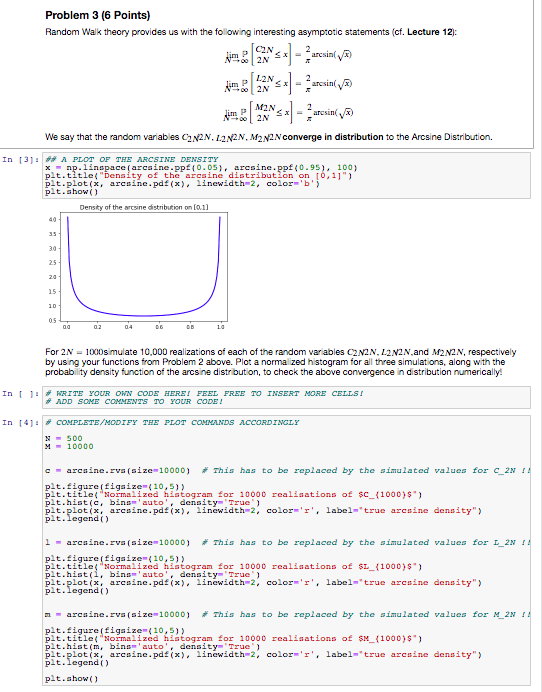
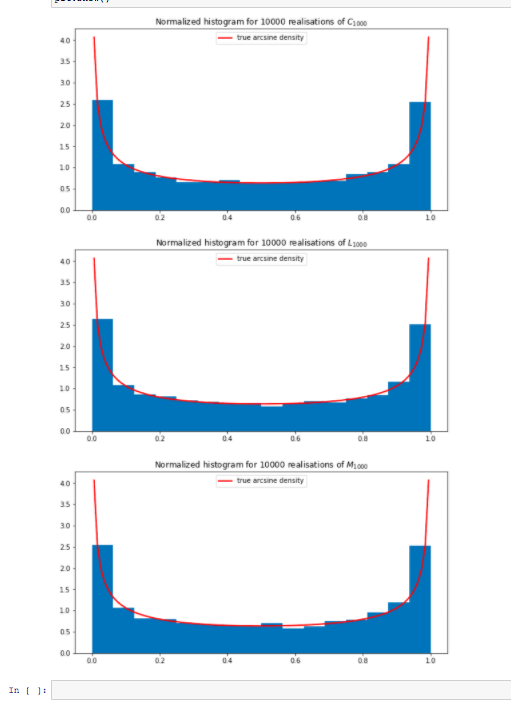
Problem 3 (6 Points) Random Walk theory provides us with the following interesting asymptotic statements (cf. Lecture 12): lim P CN 2 x - 2arcsin( y/) 160 2N 12N E x _ _ arcsin( ,/) P MIN g x - - arcsin( (x) | 2N We say that the random variables C N2N. 12/2N. My/2Nconverge in distribution to the Aresine Distribution. In [3]: ## A PLOT OF THE ARCSINE DENSITY x = np. linspace (arcaine. ppf(0.05), arcsine. ppf(0.95), 100) pit. title( "Density of the arcsine distribution on [0,1]") pit. plot (x, arcainc. pdf (x), linewidth=2, color='b' ) pit . show ( ) Density of the arcsine distribution on [on] 40 35 25 30 15 10 05 DE La For 2/ = 1000simulate 10,000 realizations of each of the random variables C2NAN. 12N2N.and M2N2N, respectively by using your functions from Problem 2 above. Plot a normal zed histogram for all three simulations, along with the probability density function of the arosine distribution, to check the above convergence in distribution numerically! In [ ]: # WRITE YOUR OWN CODE HERE! FEEL FREE TO INSERT MORE CELLSI # ADD SOME COMMENTS TO YOUR CODE! In [4]: # COMPLETE/MODIFY THE PLOT COMMANDS ACCORDINGLY 500 10000 : - arcaine. rys (size 10000) # This has to be replaced by the simulated values for C 2N plt. figure (figsize=( 10,5) ) pit. title( "Normalized histogram for 10000 realisations of sc_(1000)$") pit.hist (c, bings'auto', density 'True' ) pit. plot (x, arcmine. pdf (x), linewidth=2, colors'r', label="true arcaine density") pit . legend ( ) 1 - arcaine. rys (size 10000) # This has to be replaced by the simulated values for L 2N pit. figure ( figsize=( 10, 5) ) pit. title( "Normalized histogram for 10000 realisations of $1_(1000)$") pit. hist(1, bings'auto', density 'True' ) pit . legend ( ) pit. plot (x, arcmine. pdf(x), linewidth=2, colors'r', label="true arcaine density") a = arcaine. rys (size 10000) # This has to be replaced by the simulated values for M 2N pit. figure (figsize=( 10, 5) ) pit. hist (m, pit. title( "Normalized histogram for 10000 realisations of SM_(1000)$") pit. plot (x, , bings'auto', density 'True' ) pit . legend ( ) arcaine. pdf (x), linewidth=2, colors'r', labels"true arcaine density") pit . show ( )\f