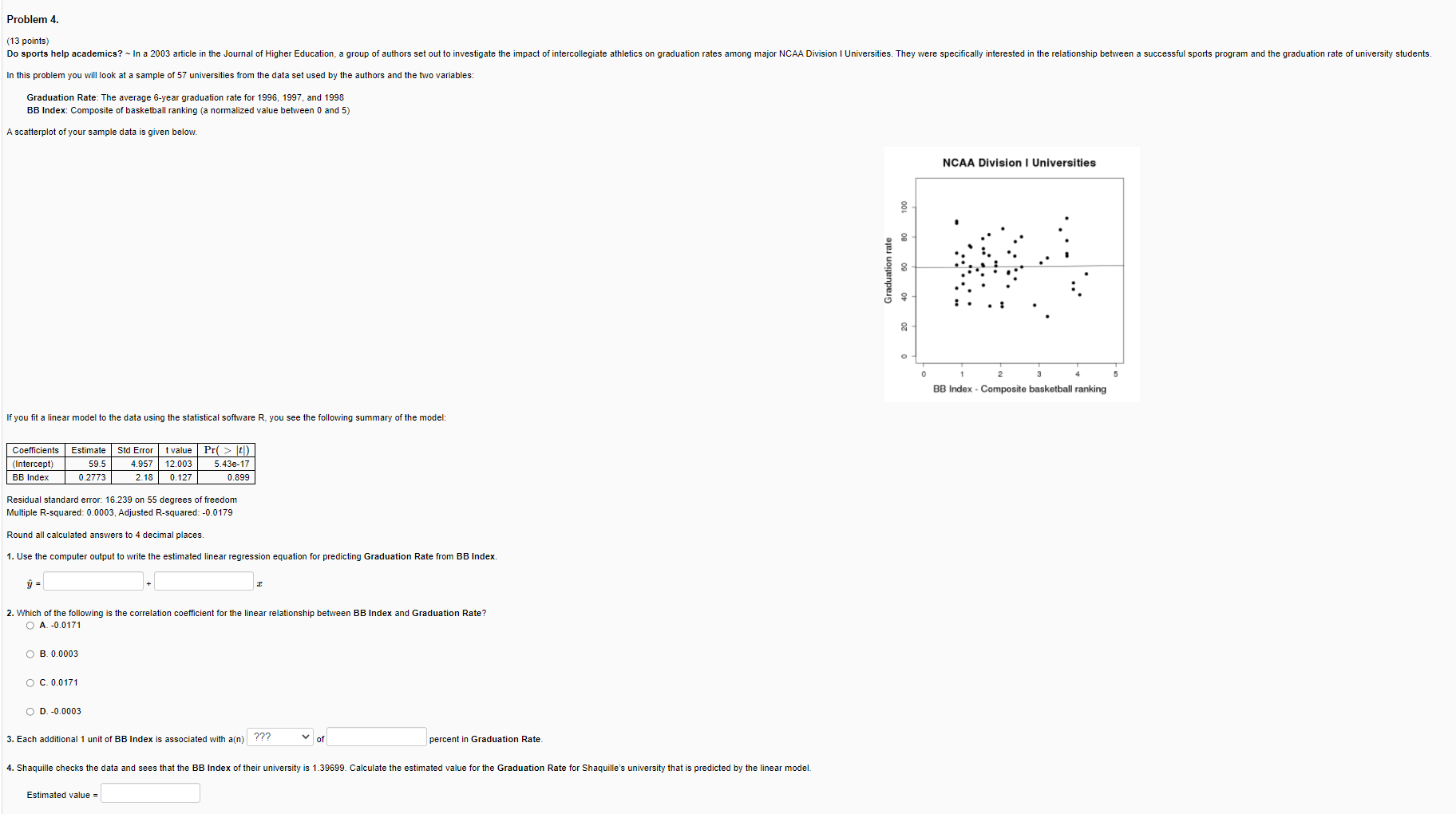
Problem 4. (13 points) Do sports help academics? ~ In a 2003 article in the Journal of Higher Education, a group of authors set out
Answered step by step
Verified Expert Solution
Question
55 users unlocked this solution today!
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1

Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
100% Satisfaction Guaranteed-or Get a Refund!
Step: 2Unlock detailed examples and clear explanations to master concepts

Step: 3Unlock to practice, ask and learn with real-world examples

See step-by-step solutions with expert insights and AI powered tools for academic success
-
 Access 30 Million+ textbook solutions.
Access 30 Million+ textbook solutions.
-
 Ask unlimited questions from AI Tutors.
Ask unlimited questions from AI Tutors.
-
 Order free textbooks.
Order free textbooks.
-
 100% Satisfaction Guaranteed-or Get a Refund!
100% Satisfaction Guaranteed-or Get a Refund!
Claim Your Hoodie Now!

Study Smart with AI Flashcards
Access a vast library of flashcards, create your own, and experience a game-changing transformation in how you learn and retain knowledge
Explore Flashcards





