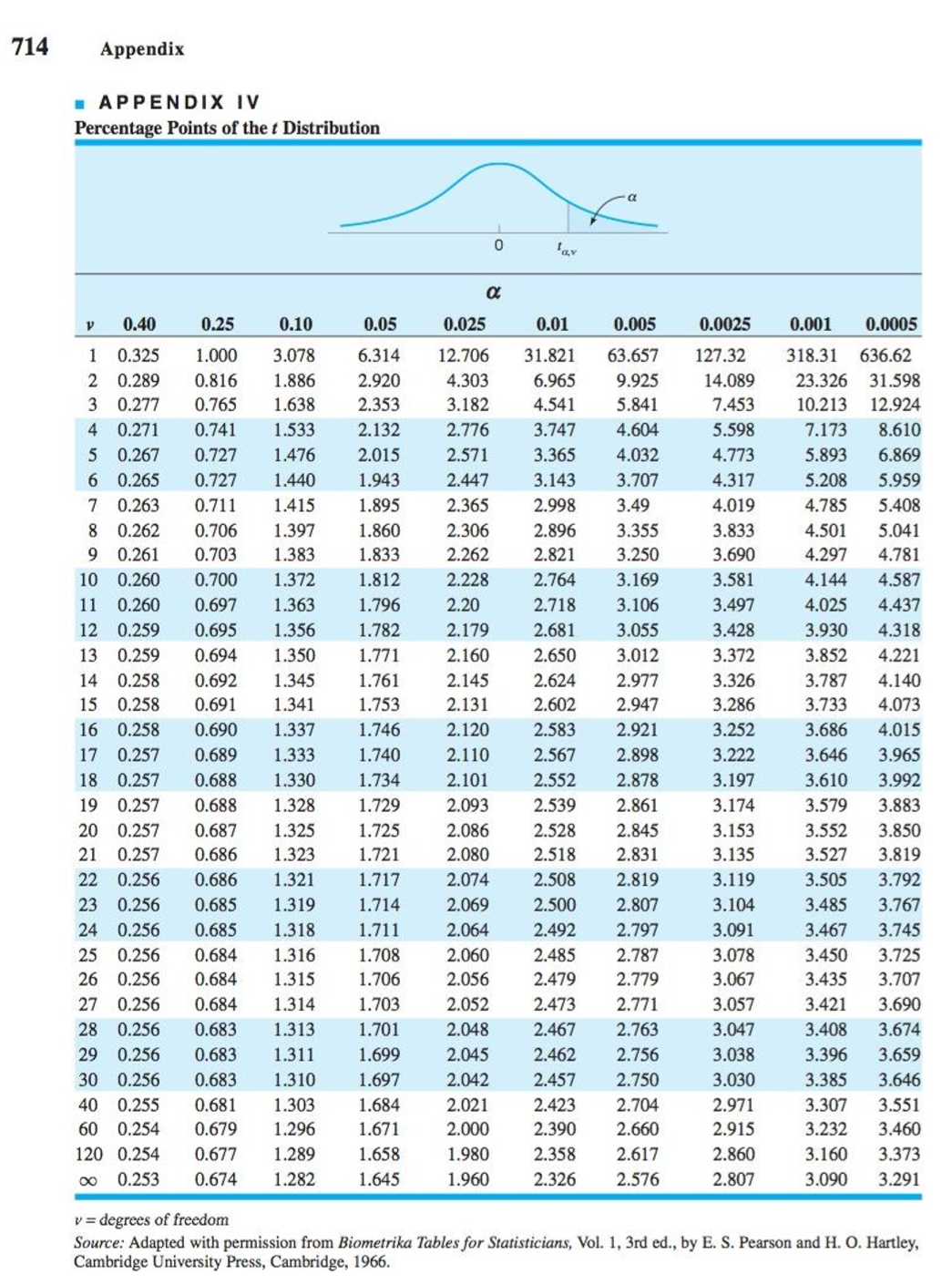
Problem 4: A machine is used to fill containers with a liquid product. Fill volume can be assumed to be normally distributed. A random sample of ten containers is selected, and the net contents (02) are as follows: 1203,1201, 1204,1202, 12.06, 11.98, 11.97, 12.02, 12.05 and 11.99. (a) Suppose that the manufacturer wants to be sure that the mean net contents exceeds 12 02. What conclusions can be drawn from the data, based on typel error =0.01. (b) What is the P-value for this test? (c) Discuss why a onesided alternative was chosen in part (a). (d) Construct a 99% two-sided confidence interval on the mean containers. 714 Appendix APPENDIX IV Percentage Points of the t Distribution av 0.40 0.25 0.025 0.01 0.005 0.0025 0.001 0.0005 0.325 1.000 3.078 6.314 12.706 63.657 127.32 318.31 0.289 0.816 1.886 2.920 4.303 6.965 9.925 14.089 23.326 31.598 0.765 1.638 2.353 3.182 4.541 5.841 12.924 0.271 0.741 1.533 2.132 2.776 3.747 4.604 5.598 7.173 8.610 1.476 2.571 4.032 4.773 5.893 6.869 0.727 1.440 1.943 2.447 3.143 3.707 4.317 5.208 5.959 0.711 1.415 1.895 2.365 2.998 5.408 0.706 2.306 2.896 3.355 3.833 4.501 5.041 0.703 1.383 1.833 2.262 2.821 3.250 3.690 4.297 4.781 10 0.260 0.700 1.372 1.812 2.228 2.764 3.581 4.144 4.587 11 0.260 0.697 1.363 1.796 2.20 3.106 4.025 4.437 12 0.259 0.695 1.782 2.179 2.681 3.055 3.428 3.930 4.318 0.694 1.350 2.160 2.650 3.012 3.372 3.852 14 0.258 0.692 1.345 1.761 2.145 2.624 2.977 15 0.258 3.326 3.787 4.140 0.691 2.131 2.947 3.286 16 0.258 4.073 0.690 1.337 1.746 2.120 2.583 2.921 3.252 3.686 4.015 1.333 2.110 2.898 3.222 3.646 18 0.257 3.965 0.688 1.330 1.734 2.101 2.552 2.878 3.197 19 0.257 3.610 3.992 0.688 1.328 2.093 2.539 2.861 3.174 20 0.257 3.579 3.883 0.687 1.325 1.725 2.086 2.528 2.845 3.153 0.686 3.552 3.850 1.721 2.080 2.518 2.831 3.135 22 0.256 3.527 3.819 0.686 1.321 1.717 2.074 2.508 2.819 3.119 23 0.256 3.505 3.792 0.685 1.319 2.069 2.500 2.807 3.104 24 0.256 3.485 3.767 0.685 1.711 2.064 2.492 2.797 0.684 3.467 3.745 2.060 2.485 2.787 3.078 26 0.256 3.450 3.725 0.684 1.315 1.706 2.056 2.479 2.779 3.067 27 0.256 3.435 3.707 0.684 1.703 2.052 2.473 2.771 3.057 3.421 3.690 0.683 1.313 1.701 2.048 2.763 3.047 3.408 0.683 3.674 1.311 1.699 2.045 2.462 2.756 3.038 3.396 30 0.256 3.659 0.683 1.697 2.042 2.457 2.750 3.030 3.385 3.646 0.681 1.684 2.021 2.423 2.704 2.971 3.307 3.551 1.296 1.671 2.000 2.660 2.915 120 0.254 3.232 3.460 0.677 1.289 1.658 1.980 2.358 2.617 2.860 3.160 3.373 0.253 1.282 1.645 1.960 3.090 3.291 v = degrees of freedom Source: Adapted with permission from Biometrika Tables for Statisticians, Vol. 1, 3rd ed., by E. S. Pearson and H. O. Hartley, Cambridge University Press, Cambridge, 1966