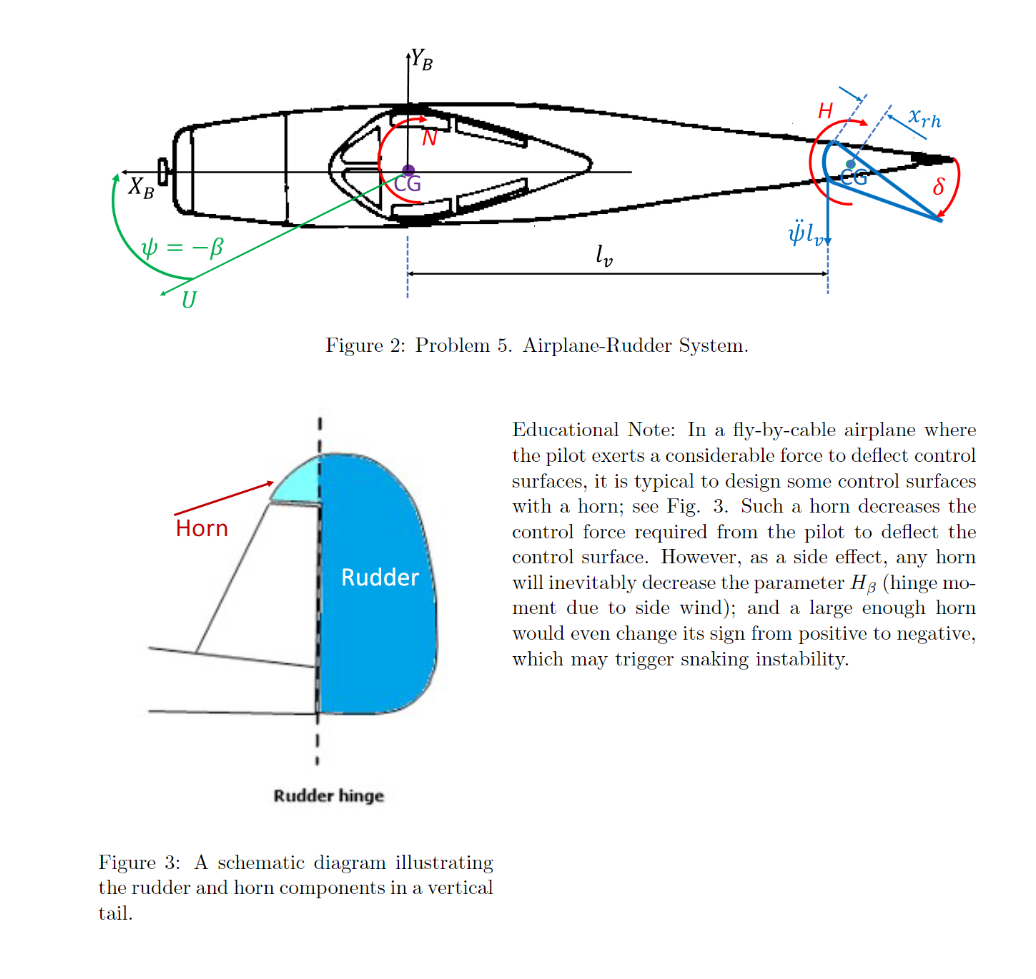
Problem 4: Figure 2 shows the top view of an airplane with its rudder control surface. In some scenarios, the airplane and its free-rudder undergo continuous oscillation during turbulence, called snaking. This behavior can be analyzed by confining the airplane's degrees of freedom to only two: the yawing motion of the airplane represented by the yaw angle between the body frame and the inertial frame; and the rudder deflection angle 8. The scenario is akin to that when the airplane is mounted on a hinge in a wind tunnel such that all degrees of freedom are prevented except the yawing motion. The airplane mass is m and its moment of inertia about the z-axis passing through the center of gravity (CG) is Iz; the rudder mass is m, and its moment of inertia about the hinge point is I. The rudder hinge is located at a distance l, behind the airplane CG and rh ahead of the rudder center of gravity, as shown in Fig. 2. The aerodynamic loads cause a yawing moment N on the airplane about its 2B-axis at the CG and a moment H about the rudder hinge. The equations of motion of the two degrees-of-freedom are given by I = N. Ir ( + 8) = H Mrlvxrh (cos + sind) The aerodynamic loads can be written as N = H = Iz ( + N + ), - Ir (H + H86 2H+H), where NB, Ns, HB, and Hs are constants that depend on the airplane geometry; b is a reference length (the wing span); and U is the forward speed. (a) Linearize these equations around = 0, 8 = 0, and write the linearized system in a state space form. Assume no control inputs. Note that the rudder deflection is state and no longer a control input. (b) Assume that Iz = 10,000kg.m, Ir = 1kg.m, m = and 1000kg, mr = 10kg, lv = 5m, xrh = 0.1m, U = 150m/s, b = 10m. NB = 20s 2, N = -30s-2, and H& = -2000s-2 Study the stability of this system when H3 = 0. (c) Show that a large negative Hg may destabilize the system. XB 4 Horn lv Figure 2: Problem 5. Airplane-Rudder System. H Xrh Rudder Educational Note: In a fly-by-cable airplane where the pilot exerts a considerable force to deflect control surfaces, it is typical to design some control surfaces with a horn; see Fig. 3. Such a horn decreases the control force required from the pilot to deflect the control surface. However, as a side effect, any horn will inevitably decrease the parameter Hg (hinge mo- ment due to side wind); and a large enough horn would even change its sign from positive to negative, which may trigger snaking instability. Rudder hinge Figure 3: A schematic diagram illustrating the rudder and horn components in a vertical tail.