Problem 4-23 (Algorithmic)

EZ-Windows, Inc., manufactures replacement windows for the home remodeling business. In January, the company produced 15,500 windows and ended the month with 9,500 windows in inventory. EZ-Windows management team would like to develop a production schedule for the next three months. A smooth production schedule is obviously desirable because it maintains the current workforce and provides a similar month-to-month operation. However, given the sales forecasts, the production capacities, and the storage capabilities as shown, the management team does not think a smooth production schedule with the same production quantity each month is possible.

	February	March	April
Sales forecast	15,500	17,000	18,500
Production capacity	15,500	13,000	19,500
Storage capacity	6,000	6,000	6,000

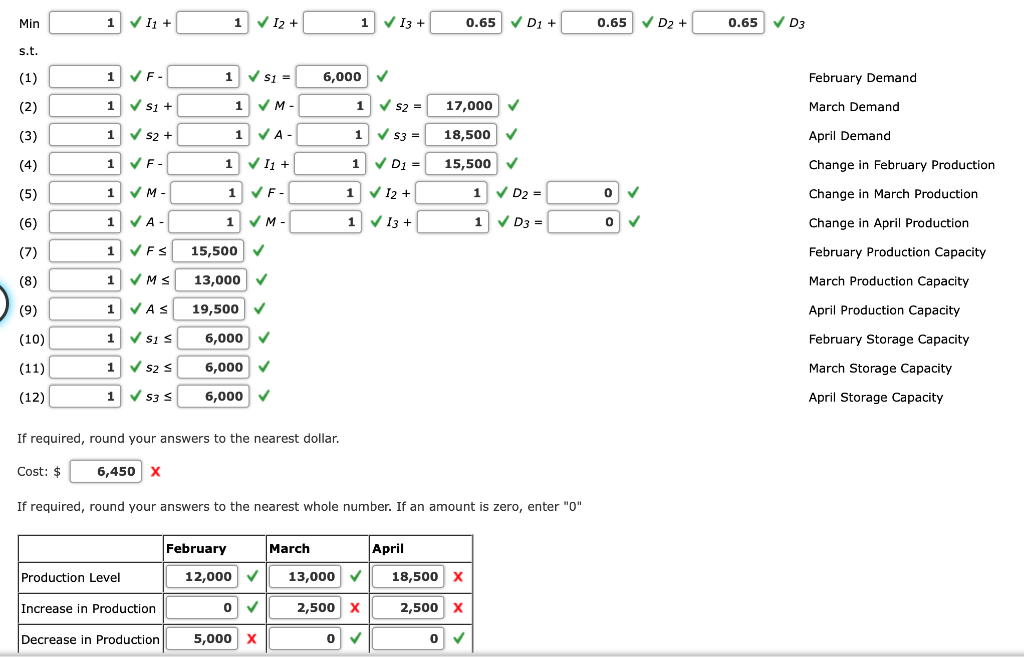
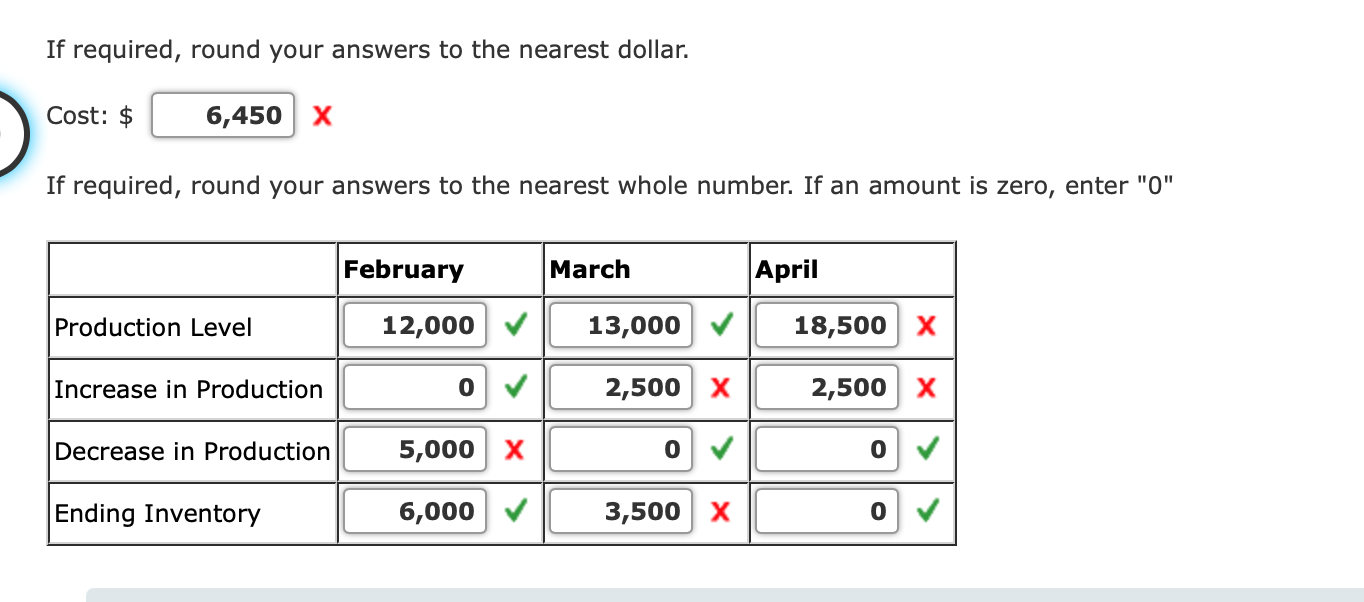
The companys cost accounting department estimates that increasing production by one window from one month to the next will increase total costs by $1.00 for each unit increase in the production level. In addition, decreasing production by one unit from one month to the next will increase total costs by $0.65 for each unit decrease in the production level. Ignoring production and inventory carrying costs, formulate and solve a linear programming model that will minimize the cost of changing production levels while still satisfying the monthly sales forecasts. If required, round your answers to two decimal places. If an amount is zero, enter "0".

Let:

F = number of windows manufactured in February

M = number of windows manufactured in March

A = number of windows manufactured in April

I_m = increase in production level necessary during month m

D_m = decrease in production level necessary during month m

s_m = ending inventory in month m

Min 1 11 + 1 12 + 1 13+ 0.65 D1 + 0.65 D2 + 0.65 D3 s.t. (1) 1 F- 1 s1 = 6,000 February Demand (2) 1 si + 1 M- 1 s2 = 17,000 March Demand (3) 1 A- 1 s3 - 18,500 April Demand 1 s2 + 1 F- (4) 1 11 + 1 D1 = 15,500 Change in February Production (5) 1 M- F 1 12 + 1 D2 = 0 Change in March Production (6) 1 A- 1 M- 1 13+ 1 D3 = 0 Change in April Production (7) 1 FS 15,500 February Production Capacity (8) 1 MS 13,000 March Production Capacity (9) 1 VAS 19,500 April Production Capacity (10) 1 Sis 6,000 February Storage Capacity (11) 1 s2 s 6,000 March Storage Capacity (12) 1 ss 6,000 April Storage Capacity If required, round your answers to the nearest dollar. Cost: $ 6,450 x If required, round your answers to the nearest whole number. If an amount is zero, enter "0" February March April Production Level 12,000 13,000 18,500 x Increase in Production 0 2,500 X 2,500 x Decrease in Production 5,000 x 0 0 If required, round your answers to the nearest dollar. Cost: $ 6,450 X If required, round your answers to the nearest whole number. If an amount is zero, enter "0" February March April Production Level 12,000 13,000 18,500 Increase in Production o 2,500 x 2,500 Decrease in Production 5,000 x 0 0 Ending Inventory 6,000 3,500 x o Min 1 11 + 1 12 + 1 13+ 0.65 D1 + 0.65 D2 + 0.65 D3 s.t. (1) 1 F- 1 s1 = 6,000 February Demand (2) 1 si + 1 M- 1 s2 = 17,000 March Demand (3) 1 A- 1 s3 - 18,500 April Demand 1 s2 + 1 F- (4) 1 11 + 1 D1 = 15,500 Change in February Production (5) 1 M- F 1 12 + 1 D2 = 0 Change in March Production (6) 1 A- 1 M- 1 13+ 1 D3 = 0 Change in April Production (7) 1 FS 15,500 February Production Capacity (8) 1 MS 13,000 March Production Capacity (9) 1 VAS 19,500 April Production Capacity (10) 1 Sis 6,000 February Storage Capacity (11) 1 s2 s 6,000 March Storage Capacity (12) 1 ss 6,000 April Storage Capacity If required, round your answers to the nearest dollar. Cost: $ 6,450 x If required, round your answers to the nearest whole number. If an amount is zero, enter "0" February March April Production Level 12,000 13,000 18,500 x Increase in Production 0 2,500 X 2,500 x Decrease in Production 5,000 x 0 0 If required, round your answers to the nearest dollar. Cost: $ 6,450 X If required, round your answers to the nearest whole number. If an amount is zero, enter "0" February March April Production Level 12,000 13,000 18,500 Increase in Production o 2,500 x 2,500 Decrease in Production 5,000 x 0 0 Ending Inventory 6,000 3,500 x o