Answered step by step
Verified Expert Solution
Question
1 Approved Answer
Two Einstein solids in thermal contact Consider two Einstein solids with NA = 4 and EA = 10 and NB = 4 and EB


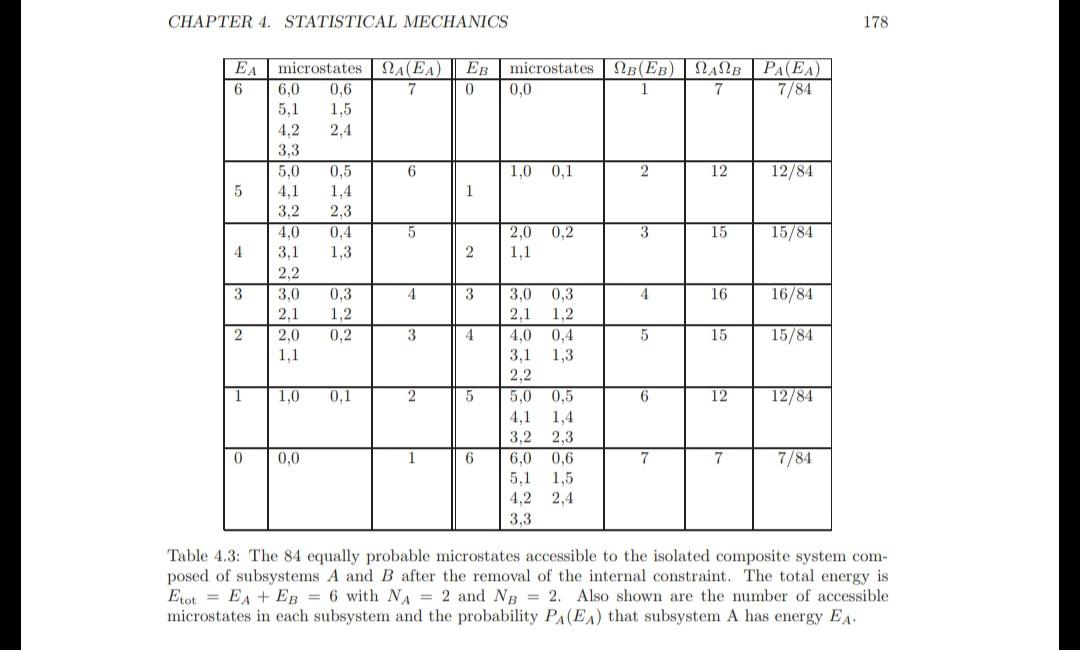
Two Einstein solids in thermal contact Consider two Einstein solids with NA = 4 and EA = 10 and NB = 4 and EB = 2. The two sub- systems are thermally isolated from one another. Verify that the number of microstates accessible to subsystem A is 286 and the number of microstates accessible to subsystem B is 10. What is the initial number of accessible microstates for the composite system? Program EinsteinSolids determines the number of accessible microstates of an Einstein solid using (4.3) and will help you answer the following questions. (a) The internal constraint is removed so that the two subsystems may exchange energy. Determine the probability PA(EA) that system A has energy EA. Plot PA versus EA and discuss its qualitative energy dependence. (b) What is the probability that energy is transferred from system A to system B and from system B to system A? What is the probability that energy goes from the hotter to the colder system? How does this probability compare to the probability found from Table 4.3 for a smaller system? Which system was hotter initially? (c) What is the number of accessible microstates for the composite system after the internal constraint has been relaxed? What is the change in the total entropy of the system (choose units such that k = 1)? (d) Determine the mean energy EA, the most probable energy EA, the standard deviations A and B, and the relative fluctuations A/EA. How does the value of this ratio compare with the value of the ratio calculated in Table 4.3? (e) The entropy of the composite system when each subsystem is in its most probable macrostate is In A (EA)B(Etot - EA). Compare the value of this contribution to the value of the total entropy, EE In A (EA)NB (Etot EA), calculated in part (c)? (f) *Consider successively larger systems and describe the qualitative behavior of the various quantities. 0 is system is = (E+N-1)! E! (N 1)! (4.3) CHAPTER 4. STATISTICAL MECHANICS EA microstates () EB microstates NB(EB) NANB 6 7 0 1 7 5 4 3 2 1 0 6,0 0.6 5,1 1,5 4,2 2,4 3.3 5,0 3,2 4,0 3,1 2,2 3,0 2,1 2,0 1,1 1,0 0,0 0,5 1,4 2,3 0,4 1,3 0,3 1,2 0,2 0,1 6 5 4 3 2 1 1 2 3 4 5 6 0,0 1,0 0,1 2,0 0,2 1,1 3,0 0,3 2,1 1,2 4,0 0,4 1,3 3,1 2,2 5,0 0,5 4,1 1,4 3,2 2,3 6,0 0,6 5.1 1,5 4,2 2.4 3,3 2 3 4 5 6 7 12 15 16 15 12 7 PA(EA) 7/84 12/84 15/84 16/84 15/84 12/84 7/84 178 Table 4.3: The 84 equally probable microstates accessible to the isolated composite system com- posed of subsystems A and B after the removal of the internal constraint. The total energy is Etot EA + EB = 6 with NA = 2 and NB = 2. Also shown are the number of accessible microstates in each subsystem and the probability PA(EA) that subsystem A has energy EA. Two Einstein solids in thermal contact Consider two Einstein solids with NA = 4 and EA = 10 and NB = 4 and EB = 2. The two sub- systems are thermally isolated from one another. Verify that the number of microstates accessible to subsystem A is 286 and the number of microstates accessible to subsystem B is 10. What is the initial number of accessible microstates for the composite system? Program EinsteinSolids determines the number of accessible microstates of an Einstein solid using (4.3) and will help you answer the following questions. (a) The internal constraint is removed so that the two subsystems may exchange energy. Determine the probability PA(EA) that system A has energy EA. Plot PA versus EA and discuss its qualitative energy dependence. (b) What is the probability that energy is transferred from system A to system B and from system B to system A? What is the probability that energy goes from the hotter to the colder system? How does this probability compare to the probability found from Table 4.3 for a smaller system? Which system was hotter initially? (c) What is the number of accessible microstates for the composite system after the internal constraint has been relaxed? What is the change in the total entropy of the system (choose units such that k = 1)? (d) Determine the mean energy EA, the most probable energy EA, the standard deviations A and B, and the relative fluctuations A/EA. How does the value of this ratio compare with the value of the ratio calculated in Table 4.3? (e) The entropy of the composite system when each subsystem is in its most probable macrostate is In A (EA)B(Etot - EA). Compare the value of this contribution to the value of the total entropy, EE In A (EA)NB (Etot EA), calculated in part (c)? (f) *Consider successively larger systems and describe the qualitative behavior of the various quantities. 0 is system is = (E+N-1)! E! (N 1)! (4.3) CHAPTER 4. STATISTICAL MECHANICS EA microstates () EB microstates NB(EB) NANB 6 7 0 1 7 5 4 3 2 1 0 6,0 0.6 5,1 1,5 4,2 2,4 3.3 5,0 3,2 4,0 3,1 2,2 3,0 2,1 2,0 1,1 1,0 0,0 0,5 1,4 2,3 0,4 1,3 0,3 1,2 0,2 0,1 6 5 4 3 2 1 1 2 3 4 5 6 0,0 1,0 0,1 2,0 0,2 1,1 3,0 0,3 2,1 1,2 4,0 0,4 1,3 3,1 2,2 5,0 0,5 4,1 1,4 3,2 2,3 6,0 0,6 5.1 1,5 4,2 2.4 3,3 2 3 4 5 6 7 12 15 16 15 12 7 PA(EA) 7/84 12/84 15/84 16/84 15/84 12/84 7/84 178 Table 4.3: The 84 equally probable microstates accessible to the isolated composite system com- posed of subsystems A and B after the removal of the internal constraint. The total energy is Etot EA + EB = 6 with NA = 2 and NB = 2. Also shown are the number of accessible microstates in each subsystem and the probability PA(EA) that subsystem A has energy EA. Two Einstein solids in thermal contact Consider two Einstein solids with NA = 4 and EA = 10 and NB = 4 and EB = 2. The two sub- systems are thermally isolated from one another. Verify that the number of microstates accessible to subsystem A is 286 and the number of microstates accessible to subsystem B is 10. What is the initial number of accessible microstates for the composite system? Program EinsteinSolids determines the number of accessible microstates of an Einstein solid using (4.3) and will help you answer the following questions. (a) The internal constraint is removed so that the two subsystems may exchange energy. Determine the probability PA(EA) that system A has energy EA. Plot PA versus EA and discuss its qualitative energy dependence. (b) What is the probability that energy is transferred from system A to system B and from system B to system A? What is the probability that energy goes from the hotter to the colder system? How does this probability compare to the probability found from Table 4.3 for a smaller system? Which system was hotter initially? (c) What is the number of accessible microstates for the composite system after the internal constraint has been relaxed? What is the change in the total entropy of the system (choose units such that k = 1)? (d) Determine the mean energy EA, the most probable energy EA, the standard deviations A and B, and the relative fluctuations A/EA. How does the value of this ratio compare with the value of the ratio calculated in Table 4.3? (e) The entropy of the composite system when each subsystem is in its most probable macrostate is In A (EA)B(Etot - EA). Compare the value of this contribution to the value of the total entropy, EE In A (EA)NB (Etot EA), calculated in part (c)? (f) *Consider successively larger systems and describe the qualitative behavior of the various quantities. 0 is system is = (E+N-1)! E! (N 1)! (4.3) CHAPTER 4. STATISTICAL MECHANICS EA microstates () EB microstates NB(EB) NANB 6 7 0 1 7 5 4 3 2 1 0 6,0 0.6 5,1 1,5 4,2 2,4 3.3 5,0 3,2 4,0 3,1 2,2 3,0 2,1 2,0 1,1 1,0 0,0 0,5 1,4 2,3 0,4 1,3 0,3 1,2 0,2 0,1 6 5 4 3 2 1 1 2 3 4 5 6 0,0 1,0 0,1 2,0 0,2 1,1 3,0 0,3 2,1 1,2 4,0 0,4 1,3 3,1 2,2 5,0 0,5 4,1 1,4 3,2 2,3 6,0 0,6 5.1 1,5 4,2 2.4 3,3 2 3 4 5 6 7 12 15 16 15 12 7 PA(EA) 7/84 12/84 15/84 16/84 15/84 12/84 7/84 178 Table 4.3: The 84 equally probable microstates accessible to the isolated composite system com- posed of subsystems A and B after the removal of the internal constraint. The total energy is Etot EA + EB = 6 with NA = 2 and NB = 2. Also shown are the number of accessible microstates in each subsystem and the probability PA(EA) that subsystem A has energy EA.
Step by Step Solution
★★★★★
3.40 Rating (162 Votes )
There are 3 Steps involved in it
Step: 1
a We determine the probability PA EA w we have AB 4 E EATER a tov 3 6741 6...
Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


