Problem 7.18 (a) Solve the following problems by reducing to the original max-flow problem

Algorithms [Dasgupta, Papadimitriou, Vazirani][DPV] 1st edition

There are many common variations of the maximum flow problem. Here are four of them.

Solve the following problems by reducing to the original max-flow problem. In other words, explain how to solve the new flow variant problem using an algorithm for solving max-flow as a black-box. Explain how to take an input for the new problem and define an input for the original max-flow problem. Then given a max-flow F* to this input you just defined, explain how to get the solution to the new problem.

describe your algorithm in words; no pseudocode.

(a) There are many sources and many sinks, and we wish to maximize the total flow from all sources to all sinks

my answer: (not sure if #5 is enough to satisfy the multi Source/Sink and is the steps for max-flow are 100% correct in 1-4)

1. Start with a directed graph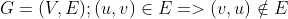

2. Find f_e for all 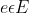a valid flow of maximum capacity

3. capacity constraint for all 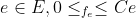and flow-in to V = flow-out of V.

4. using BFS algorithm over a subset of the graph to find a valid flow of maximum capacity in 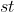path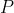

5. to compensate for the multiple sources and sinks we add and artificial Source s and an artificial Sink 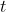which connects to all sources and sinks.

running time: this is reduced to the max-flow problem therefore the run time is O(|E|) for all edges explored and O(|V|) for all vertices explored so the total run time is O(|V|+|E|).

st st