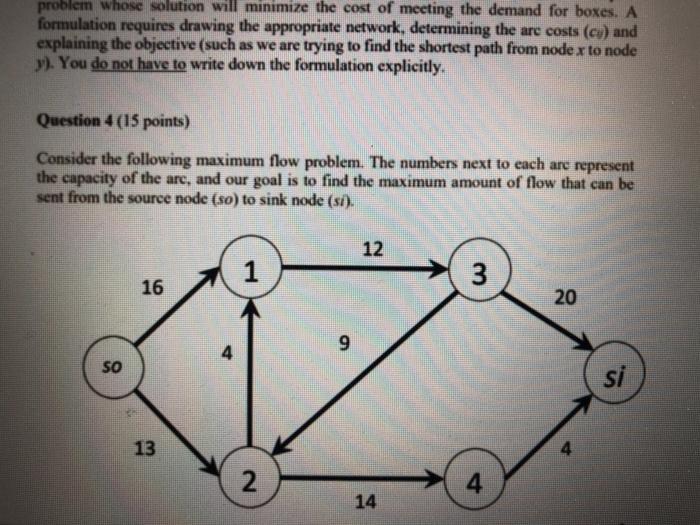
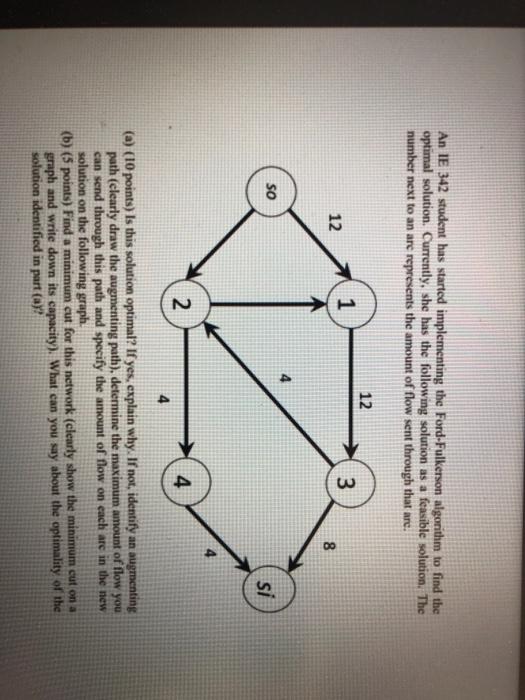
problem whose solution will minimize the cost of meeting the demand for boxes. A formulation requires drawing the appropriate network, determining the arc costs (cy) and explaining the objective (such as we are trying to find the shortest path from nodex to node y). You do not have to write down the formulation explicitly. Question 4 (15 points) Consider the following maximum flow problem. The numbers next to each are represent the capacity of the arc, and our goal is to find the maximum amount of flow that can be sent from the source node (so) to sink node (si). 12 1 3 16 20 9 4 SO si 13 2 4 14 An IE 342 student has started implementing the Ford-Fulkerson algorithm to find the optimal solution. Currently, she has the following solution as a feasible solution. The number next to an are represents the amount of flow sent through that are 12 1 3 12 8 SO si 2 4 4 (a) (10 points) Is this solution optimal? If yes, explain why. If not, identify an augmenting path (clearly draw the augmenting path), determine the maximum amount of flow you can send through this path and specify the amount of flow on each are in the new solution on the following graph. (b) (5 points) Find a minimum cut for this network (clearly show the minimum cut on a graph and write down its capacity). What can you say about the optimality of the solution identified in part(a)? problem whose solution will minimize the cost of meeting the demand for boxes. A formulation requires drawing the appropriate network, determining the arc costs (cy) and explaining the objective (such as we are trying to find the shortest path from nodex to node y). You do not have to write down the formulation explicitly. Question 4 (15 points) Consider the following maximum flow problem. The numbers next to each are represent the capacity of the arc, and our goal is to find the maximum amount of flow that can be sent from the source node (so) to sink node (si). 12 1 3 16 20 9 4 SO si 13 2 4 14 An IE 342 student has started implementing the Ford-Fulkerson algorithm to find the optimal solution. Currently, she has the following solution as a feasible solution. The number next to an are represents the amount of flow sent through that are 12 1 3 12 8 SO si 2 4 4 (a) (10 points) Is this solution optimal? If yes, explain why. If not, identify an augmenting path (clearly draw the augmenting path), determine the maximum amount of flow you can send through this path and specify the amount of flow on each are in the new solution on the following graph. (b) (5 points) Find a minimum cut for this network (clearly show the minimum cut on a graph and write down its capacity). What can you say about the optimality of the solution identified in part(a)