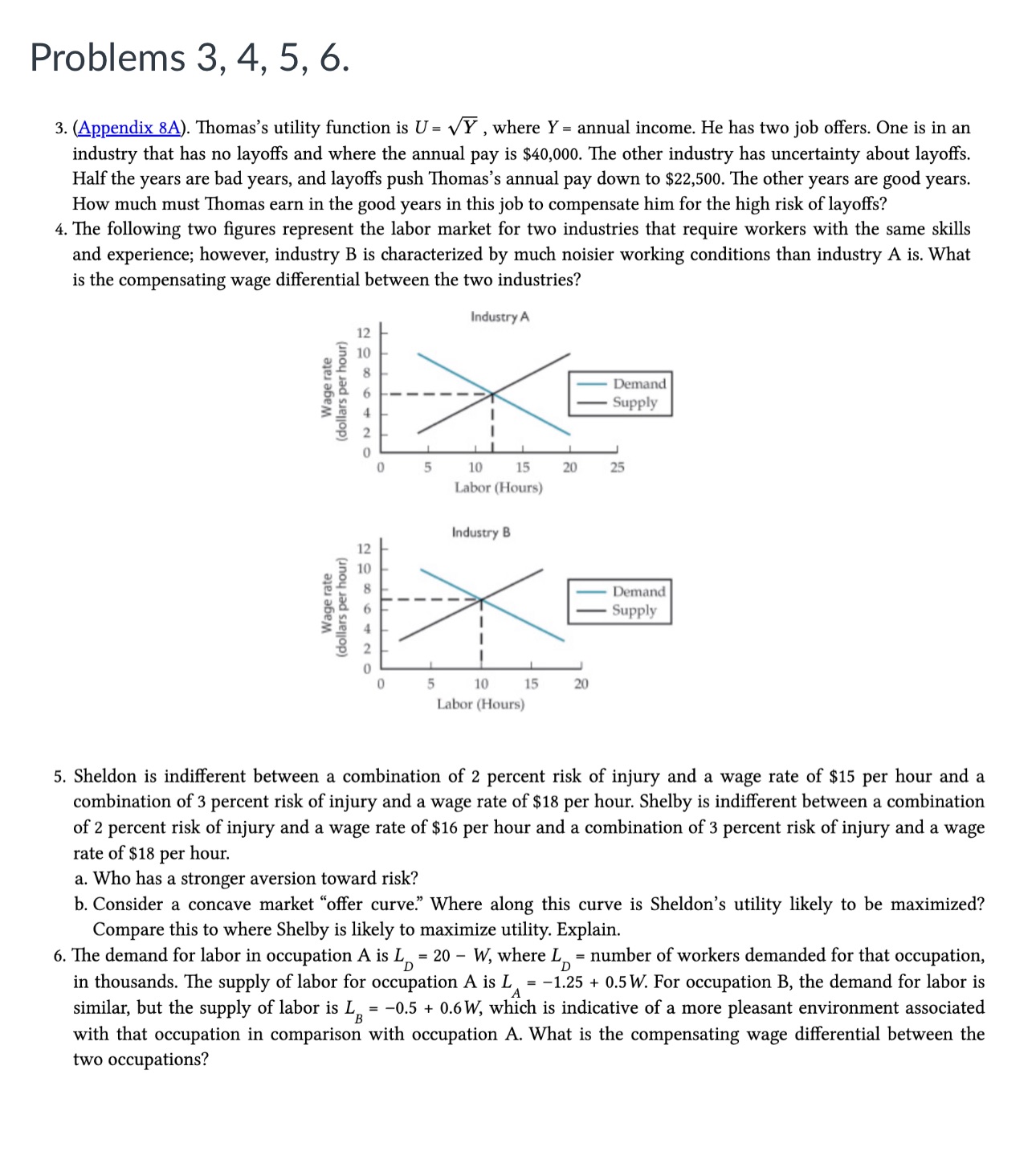
Problems 3, 4, 5, 6. 3. (Appendix 8A). Thomas''s utility function is U= /Y , where Y = annual income. He has two job offers. One is in an industry that has no layoffs and where the annual pay is $40,000. The other industry has uncertainty about layoffs. Half the years are bad years, and layoffs push Thomas's annual pay down to $22,500. The other years are good years. How much must Thomas earn in the good years in this job to compensate him for the high risk of layoffs? 4. The following two figures represent the labor market for two industries that require workers with the same skills and experience; however, industry B is characterized by much noisier working conditions than industry A is. What is the compensating wage differential between the two industries? Industry A Demand Supply Wage rate (dollars per hour) 0 5 10 15 20 25 Labor (Hours) Industry B Demand Supply Wage rate (dollars per hour 0 5 10 15 20 Labor (Hours) 5. Sheldon is indifferent between a combination of 2 percent risk of injury and a wage rate of $15 per hour and a combination of 3 percent risk of injury and a wage rate of $18 per hour. Shelby is indifferent between a combination of 2 percent risk of injury and a wage rate of $16 per hour and a combination of 3 percent risk of injury and a wage rate of $18 per hour. a. Who has a stronger aversion toward risk? b. Consider a concave market \"offer curve\" Where along this curve is Sheldon's utility likely to be maximized? Compare this to where Shelby is likely to maximize utility. Explain. 6. The demand for labor in occupation A is L =20-W, where Ly number of workers demanded for that occupation, in thousands. The supply of labor for occupation A is LA = 1.25 + 0.5 W. For occupation B, the demand for labor is similar, but the supply of labor is L, =-05+06W, which is indicative of a more pleasant environment associated with that occupation in comparison with occupation A. What is the compensating wage differential between the two occupations