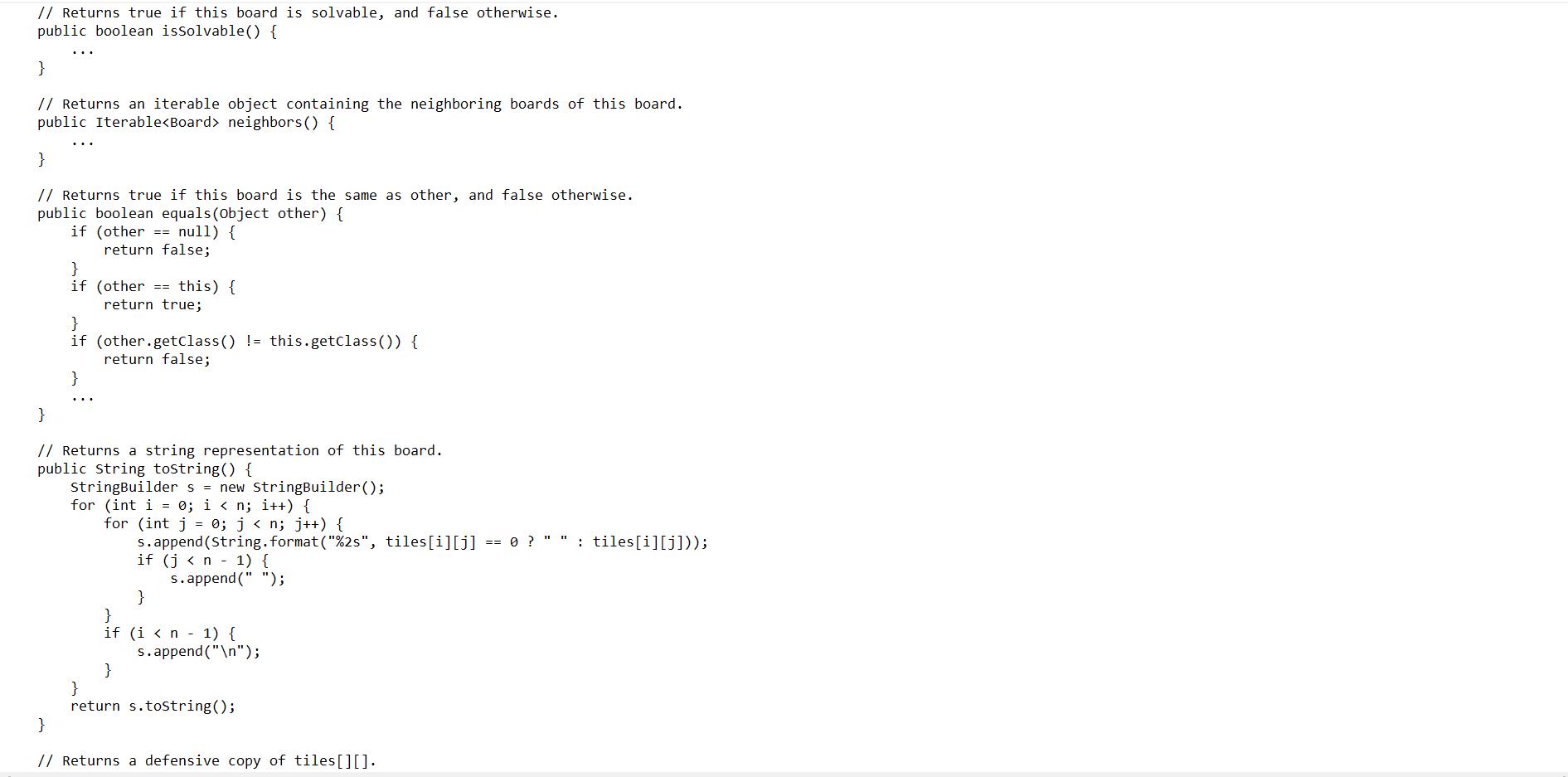
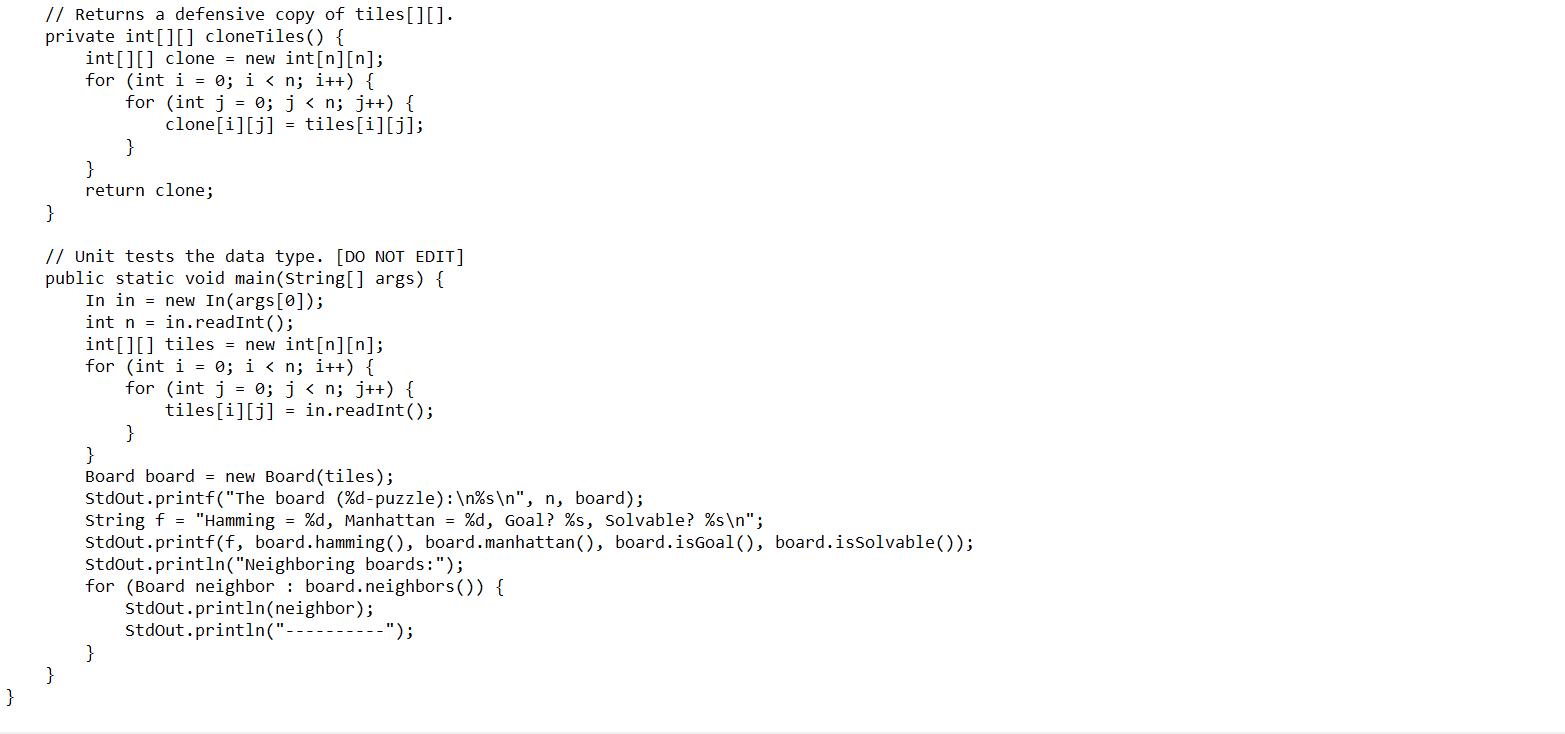
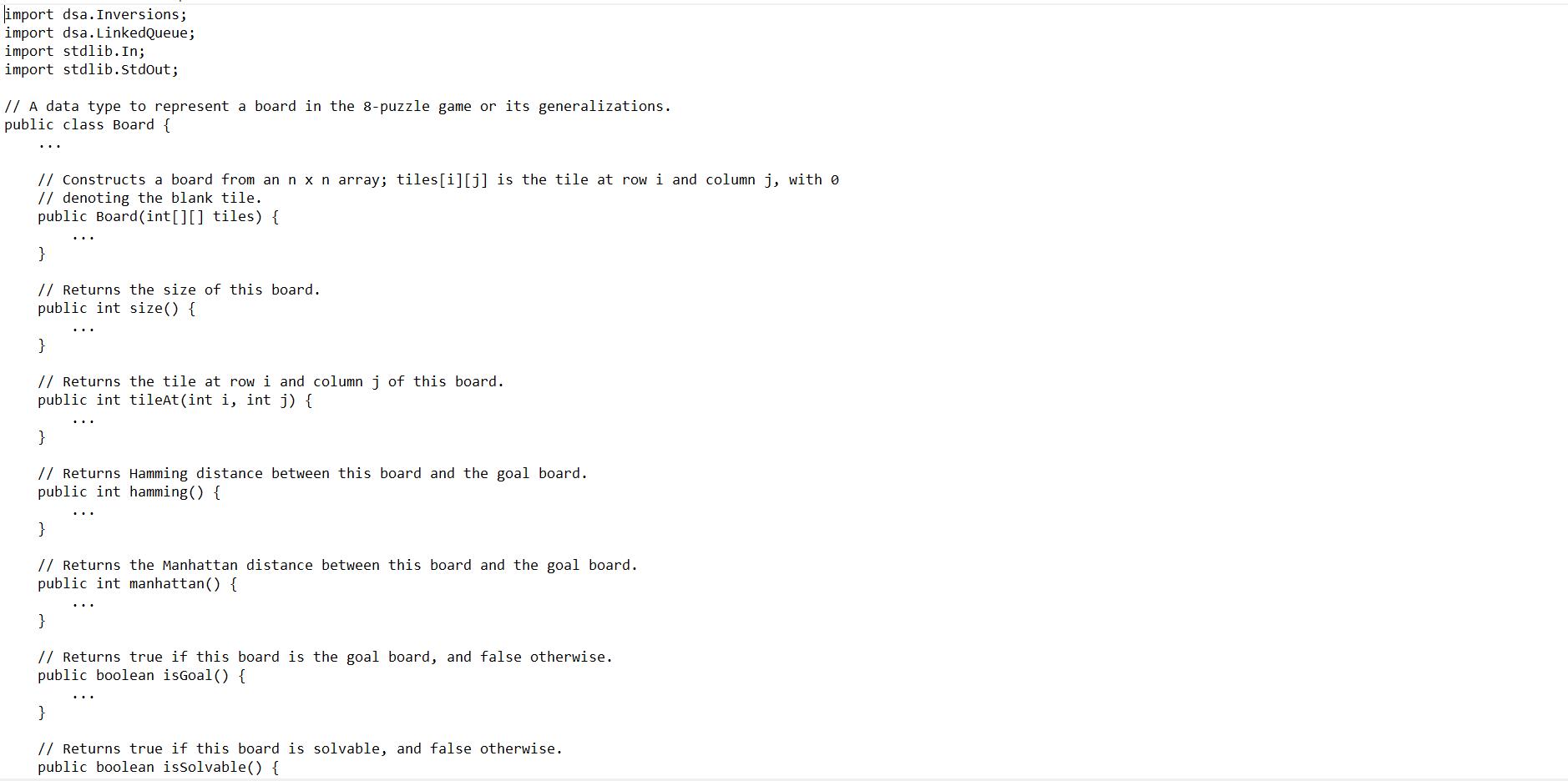
Problems Goal The purpose of this project is to write a program to solve the 8-puzzle problem (and its natural generalizations) using the A* search algorithm. The Problem The 8-puzzle problem is a puzzle invented and popularized by Noyes Palmer Chapman in the 1870s. It is played on a 3-by-3 grid with 8 square blocks labeled 1 through 8 and a blank square. Your goal is to rearrange the blocks so that they are in order. You are permitted to slide blocks horizontally or vertically into the blank square. The following shows a sequence of legal moves from an initial board position (left) to the goal position (right). 1 3 4 2 5 7 8 6 initial 8 1 4 7 1 6 2 7 8 3 2 5 initial 356 Best-First Search Now, we describe a solution to the problem that illustrates a general artificial intelligence methodology known as the A* search algorithm. We define a search node of the game to be a board, the number of moves made to reach the board, and the previous search node. First, insert the initial search node (the initial board, 0 moves, and a null previous search node) into a priority queue. Then, delete from the priority queue the search node with the minimum priority, and insert onto the priority queue all neighboring search nodes (those that can be reached in one move from the dequeued search node). Repeat this procedure until the search node dequeued corresponds to a goal board. The success of this approach hinges on the choice of priority function for a search node. We consider two priority functions: 1 2 4 7 Hamming priority function. The sum of the Hamming distance (number of tiles in the wrong position), plus the number of moves made so far to get to the search node. Intuitively, a search node with a small number of tiles in the wrong position is close to the goal, and we prefer a search node that have been reached using a small number of moves. 1 2 3 5 6 8 7 8 Manhattan priority function. The sum of the Manhattan distance (sum of the vertical and horizontal distance) from the tiles to their goal positions, plus the number of moves made so far to get to the search node. For example, the Hamming and Manhattan priorities of the initial search node below are 5 and 10, respectively. goal 356 1 2 3 4 5 7 8 6 1 2 3 4 5 6 7 8 goal 1 2 3 4 5 6 7 8 1 1 0 1 50 1 1 0 0 Hamming 1 2 3 4 5 6 7 8 1 2002 203 Manhattan 10+ 0 We make a key observation: To solve the puzzle from a given search node on the priority queue, the total number of moves we need to make (including those already made) is at least its priority, using either the Hamming or Manhattan priority function. (For Hamming priority, this is true because each tile that is out of place must move at least once to reach its goal position. For Manhattan priority, this is true because each tile must move its Manhattan distance from its goal position. Note that we do not count the blank square when computing the Hamming or Manhattan priorities.) Consequently, when the goal board is dequeued, we have discovered not only a sequence of moves from the initial board to the goal board, but one that makes the fewest number of moves. Challenge for the mathematically inclined: prove this fact. A Critical Optimization Best-first search has one annoying feature: search nodes corresponding to the same board are enqueued on the priority queue many times. To reduce unnecessary exploration of useless search nodes, when considering the neighbors of a search node, don't enqueue a neighbor if its board is the same as the board of the previous search node. 8 4 7 13 2 5 6 previous 81 3 4 2 7 6 5 search node 81 4 2 7 6 neighbor 3 5 81 3 4 2 7 6 5 neighbor (disallow) 8 1 3 42 5 7 6 neighbor Project 4 (8 Puzzle) A Second Optimization To avoid recomputing the Hamming/Manhattan distance of a board (or, alternatively, the Ham- ming/Manhattan priority of a solver node) from scratch each time during various priority queue operations, compute it at most once per object; save its value in an instance variable; and return the saved value as needed. This caching technique is broadly applicable: consider using it in any situation where you are recomputing the same quantity many times and for which computing that quantity is a bottleneck operation. Game Tree One way to view the computation is as a game tree, where each search node is a node in the game tree and the children of a node correspond to its neighboring search nodes. The root of the game tree is the initial search node; the internal nodes have already been processed; the leaf nodes are maintained in a priority queue; at each step, the A* algorithm removes the node with the smallest priority from the priority queue and processes it (by adding its children to both the game tree and the priority queue). manhattan - 3 moves = 1 priority=4 manhattan - 4 moves - 0 priority 4 next search node processed 1 - 4 2 7 8 3 5 6 previ initial search node - 1 4 7 2 5 8 6 2/9 manhattan - 5 moves - 1 priority - 6 25 7 8 6 currently on PQ 2 3 5 6 87 0041 manhattan - 4 moves - 2 priority - 6 12 34 5 6 7 8 9 10 11 12 13 15 14 86 not added to PQ (critical optimization) row-major order: 3 1 2 3 5 6 87 manhattan - 3 moves = 1 priority 4 1 2 3 4 5 6 87 inversions - 1 (8-7) manhattan - 2 moves - 2 priority - 4 next search node processed 1 4 7 1 2 3 4 5 6 8 7 2 manhattan - 4 moves - 0 priority - 4 8 1 2 3 4 5 6 87 3 1 2 3 4-5 786 currently on PQ (will be processed next) inversions 1 (8-7) 5 6 Detecting Unsolvable Puzzles Not all initial boards can lead to the goal board by a sequence of legal moves, including the two below: initial search node 1 3 2 5 6 4 7 To detect such situations, use the fact that boards are divided into two equivalence classes with respect to reachability: those that lead to the goal board; and those that cannot lead to the goal board. Moreover, we can identify in which equivalence class a board belongs without attempting to solve it. 1 2 3 4 6 8 5 7 manhattan - 4 moves -2 priority - 6 Odd board size. Given a board, an inversion is any pair of tiles i and j where i < j but i appears after j when considering the board in row-major order (row 0, followed by row 1, and so forth). 8 00 previous board manhattan - 5 moves - 1 priority - 6 1 2 3 4 6 857 inversions 3 (6-5 8-5 8-7) 1 4 3 2 5 786 currently on PQ 25 786 currently on PQ 1 2 3 4 6 8 5 7 1 2 3 46857 inversions 3 (6-5 8-5 8-7) 1 2 3 8 4 6 5 7 1 2 3 8 4 657 5 inversions (8-4 8-6 8-5 8-7 6-5) 3/9 If the board size n is an odd integer, then each legal move changes the number of inversions by an even number. Thus, if a board has an odd number of inversions, then it cannot lead to the goal board by a sequence of legal moves because the goal board has an even number of inversions (zero). The converse is also true: if a board has an even number of inversions, then it can lead to the goal board by a sequence of legal moves. row-major order: 2 1 3 4 5 6 8 9 10 7 11 13 14 15 12 blank row - 1 inversions - 6 sum - 7 Board Board (int[][] tiles) 1 4 2 78 int size() int tileAt (int i, int j) int hamming () int manhattan () boolean isGoal() boolean isSolvable() 3 5 6 1 3 4 2 5 7 86 inversions - 4 (3-2 4-2 7-6 8-6) Iterable neighbors () boolean equals (Object other) String toString() 1 3 2 5 7 8 6 Project 4 (8 Puzzle) 4 1 2 3 4 5 6 8 9 10 7 11 13 14 15 12 sun - 7 Performance Requirements blank row - 1 inversions 6 => 1 3 4 2 57 86 inversions - 4 (3-2 4-2 7-6 8-6) 1 2 3 5 7 8 6 Even board size. If the board size n is an even integer, then the parity of the number of inversions is not invariant. However, the parity of the number of inversions plus the row of the blank square is invariant: each legal move changes this sum by an even number. If this sum is even, then it cannot lead to the goal board by a sequence of legal moves; if this sum is odd, then it can lead to the goal board by a sequence of legal moves. 1 2 3 4 5 7 86 inversions - 2 (7-68-6) => 1 2 3 4 5 6 7 8 9 10 11 13 14 15 12 blank row - 2 inversions 3 sum - 5 1 2 3 5 7 8 6 1 2 3 4 5 7 86 inversions 2 (7-6 8-6) 1 2 3 4 5 6 7 8 9 10 11 13 14 15 12 blank row - 2 inversions - 3 sum 5 1 4 7 8 2 3 5 6 returns true if this board is the goal board, and false otherwise returns true if this board solvable, and false otherwise 1 2 3 4 5 6 7 8 Problem 1. (Board Data Type) Implement an immutable data type called Board to represent a board in an n-puzzle, supporting the following API: inversions - 0 12 3 5 6 7 8 9 10 11 12 13 14 15 blank rou -3 inversions - 0 sum 3 constructs a board from an n x n array; tiles[i][j] is the tile at row i and column j, with 0 denoting the blank tile returns the size of this board size returns the tile at row i and column returns Hamming distance between this board and the goal board returns the Manhattan distance between this board and the goal board returns an iterable object containing the neighboring boards of this board returns true if this board is the same as other, and false otherwise returns a string representation of this board Performance Requirements The constructor should run in time T(n) ~ n, where n is the board size. The size(), tileAt (), hamming (), manhattan (), and isGoal() methods should run in time T(n) ~ 1. The issolvable() method should run in time T(n) ~ n log n. The neighbors () and equals() methods should run in time T(n) ~ n. >_/workspace/project4 $ java Board data/puzzle05.txt The board (3-puzzle): 4 1 3 26 75 8 Hamming Neighboring boards: 4 1 3 726 5 8 13 426 75 8 4 1 3 2 6 758 5, Manhattan 5, Goal? false, Solvable? true Sjava Board data/puzzle 4x4-unsolvable1.txt The board (4-puzzle): 3 2 4 8 16 12 5 10 7 11 9 13 14 15 Hamming 12, Manhattan 13, Goal? false, Solvable? false Neighboring boards: 3 2 4 8 1 67 12 5 10 11 9 13 14 15 3 2 Project 4 (8 Puzzle) 8 4/9 > "/workspace/project4 $ java Board data/puzzle05.txt The board (3-puzzle): 4 1 3 26 75 8 Hamming 5, Manhattan - 5, Goal? false, Solvable? true Neighboring boards: 4 13 7 26 5 8 13 426 7 58 4 1 3 2 6 758 Sjava Board data/puzzle4x4-unsolvable1.txt The board (4-puzzle): 324 8 1 6 12 5 10 7 11 9 13 14 15 Hamming 12, Manhattan - 13, Goal? false, Solvable? false Neighboring boards: 3 2 4 8 16 7 12 5 10 11 9 13 14 15 32 8 16 4 12 5 10 7 11 9 13 14 15 3 24 8 16 12 5 10 7 11 9 13 14 15 324 8 1 6 12 5 10 7 11 9 13 14 15 Before you write any code, make sure you thoroughly understand the concepts that are central to solving the 8-puzzle and its generalizations using the A* algorithm. Compute the following for the two initial boards A and B shown below: 4 7 A 1 3 2 6 5 8 1. Hamming distance of the board to the goal board 2. Manhattan distance of the board to the goal board B 1 2 3 4 6 5 7 8 Before you write any code, make sure you thoroughly understand the concepts that are central to solving the 8-puzzle and its generalizations using the A* algorithm. Compute the following for the two initial boards A and B shown below: 4 Instance variables: 7 1. Hamming distance of the board to the goal board 2. Manhattan distance of the board to the goal board 3. Neighboring boards of the board 4. Row-major order of the board 5. Position of the blank tile (in row-major order) in the board 6. Number of inversions (excluding the blank tile) for the board 7. Is the board solvable? Explain why or why not A 1 3 2 6 5 8 8. A shortest solution for the board, if one exists Directions: Board (int[ tiles) Project 4 (8 Puzzle) - Tiles in the board, int [][] tiles. - Board size, int n. - Hamming distance to the goal board, int hamming. - Manhattan distance to the goal board, int manhattan. - Position of the blank tile in row-major order, int blankPos. private int [][] cloneTiles() Return a defensive copy of the tiles of the board. B 1 2 3 4 6 5 7 8 5/9 neturn a defensive copy the thes of the board. Board(int[] tiles) - Initialize the instance variables this.tiles and a to tiles and the number of rows in tiles respectively. n - Compute the Hamming/Manhattan distances to the goal board and the position of the blank tile in row-major order, and store the values in the instance variables hamming, manhattan, and blankPos respectively. int size() Return the board size. int tilekt(int i, int j) Return the tile at row i and column j. int hamming () - Return the Hamming distance to the goal board. int manhattan () Return the Manhattan distance to the goal board. boolean isGoal () Return true if the board is the goal board, and false otherwise. boolean isSolvable() Create an array of size n - 1 containing the tiles (excluding the blank tile) of the board in row-major order. - Use Inversions.count() to compute the number of inversions in the array. From the number of inversions, compute and return whether the board is solvable. Iterable neighbors () Create a queue q of Board objects. For each possible neighbor of the board (determined by the blank tile position): *Clone the tiles of the board. * Exchange an appropriate tile with the blank tile in the clone. * Construct a Board object from the clone, and enqueue it into q. Return q. boolean equals(Board other) Return true if the board is the same as other, and false otherwise. // Returns true if this board is solvable, and false otherwise. public boolean issolvable() { } // Returns an iterable object containing the neighboring boards of this board. public Iterable neighbors() { } // Returns true if this board is the same as other, and false otherwise. public boolean equals(Object other) { if (other == null) { return false; } if (other == this) { return true; } if (other.getclass () != this.getClass()) { return false; } } // Returns a string representation of this board. public string tostring() { StringBuilder s = new StringBuilder(); for (int i = 0; i } // Returns a defensive copy of tiles [][]. private int [][] cloneTiles () { int[][] clone = new int[n][n]; for (int i=0; i import dsa. Inversions; import dsa.LinkedQueue; import stdlib.In; import stdlib.stdout; // A data type to represent a board in the 8-puzzle game or its generalizations. public class Board { ... // Constructs a board from an n x n array; tiles[i][j] is the tile at row i and column j, with 0 // denoting the blank tile. public Board (int[][] tiles) { } // Returns the size of this board. public int size() { } // Returns the tile at row i and column j of this board. public int tileAt(int i, int j) { } // Returns Hamming distance between this board and the goal board. public int hamming () { } // Returns the Manhattan distance between this board and the goal board. public int manhattan () { } // Returns true if this board is the goal board, and false otherwise. public boolean isGoal() { } // Returns true if this board is solvable, and false otherwise. public boolean issolvable() {