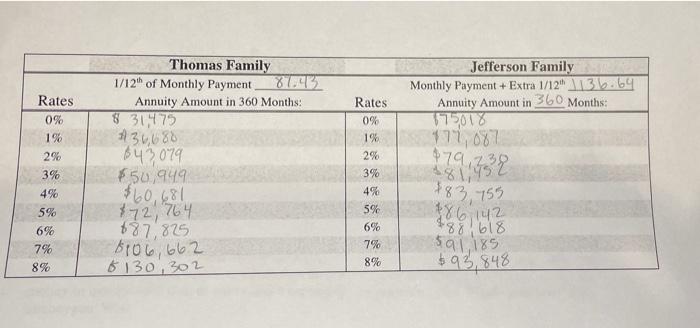
Procedure: In our brief case study, we assume the Thomas and Jefferson families have identical mortgages (30-year term, fixed-rate 6% APR, and a loan amount of $175,000). The Thomas family will not pay extra but the Jeffersons will. Follow the steps below prior to your analysis. 1. Using the Payment mini calculator of the Financial Toolboxes spreadsheet, calculate the mortgage payment (the same for both families). Required Monthly Payment = $ 2. Assume that the Thomas's will make only the required mortgage payment. The Jeffersons, however, would like to pay off their loan carly. They decide to make the equivalent of an extra payment each year by adding an extra 1/12 of the payment to the required amount. Complete the following calculations to find what they plan to pay each month: a. 1/12 of the required monthly payment = $ b. By adding this 1/12 to the required payments, the Jeffersons plan to pay $ each month 3. The Thomas's will take the full 30 years to pay off their loan, since they are making only the required payments. The Jefferson's extra payment amount, on the other hand, will allow them to pay off their loan more rapidly. Use the Years mini financial calculator of the Financial Toolbox spreadsheet to calculate the approximate number of years (nearest 10) it would take the Jeffersons to pay off their loan. Number of years to pay off loan Rates 0% 1% 2% 3% Jefferson Family Monthly Payment + Extra 1/12A136.69 Annuity Amount in 360 Months: 179018 174,087 Thomas Family 1/12 of Monthly Payment Annuity Amount in 360 Months: $ 30,475 36,680 643079 $50,949 $60,681 872, 764 087.875 8106, 662 6130,302 Rates 0% 1% 2% 3% 4% 5% 6% 7% 8% 479,732 4% 5% 6% 7% 8% 183, 755 186, 142 188,618 591,185 $93, 848 Discussion: 1. What generalizations can you make from the annuity amounts reflected in the analysis table above with regards to the different strategies taken by the families? That is, from a purely financial aspect of the calculations in your table what generalizations could you make regarding the two different strategies? 1 5. Note the dates of the advice columns. How might market performance figure in to their advice they gave at that time? 6. Why do you think Sharon Epperson's advice at the end specifically calls attention to an assumption of whether you are "debt-free and maxing out your 401(k) and IRAs?" 7. If you were to pay extra principal on a mortgage, when is the best time to do it (early or later in the loan process) and why? 8. When you pay extra principal on a loan, describe whether you feel you are actually earning interest on that money or not. That is, how does the old adage "a penny saved is a penny Procedure: In our brief case study, we assume the Thomas and Jefferson families have identical mortgages (30-year term, fixed-rate 6% APR, and a loan amount of $175,000). The Thomas family will not pay extra but the Jeffersons will. Follow the steps below prior to your analysis. 1. Using the Payment mini calculator of the Financial Toolboxes spreadsheet, calculate the mortgage payment (the same for both families). Required Monthly Payment = $ 2. Assume that the Thomas's will make only the required mortgage payment. The Jeffersons, however, would like to pay off their loan carly. They decide to make the equivalent of an extra payment each year by adding an extra 1/12 of the payment to the required amount. Complete the following calculations to find what they plan to pay each month: a. 1/12 of the required monthly payment = $ b. By adding this 1/12 to the required payments, the Jeffersons plan to pay $ each month 3. The Thomas's will take the full 30 years to pay off their loan, since they are making only the required payments. The Jefferson's extra payment amount, on the other hand, will allow them to pay off their loan more rapidly. Use the Years mini financial calculator of the Financial Toolbox spreadsheet to calculate the approximate number of years (nearest 10) it would take the Jeffersons to pay off their loan. Number of years to pay off loan Rates 0% 1% 2% 3% Jefferson Family Monthly Payment + Extra 1/12A136.69 Annuity Amount in 360 Months: 179018 174,087 Thomas Family 1/12 of Monthly Payment Annuity Amount in 360 Months: $ 30,475 36,680 643079 $50,949 $60,681 872, 764 087.875 8106, 662 6130,302 Rates 0% 1% 2% 3% 4% 5% 6% 7% 8% 479,732 4% 5% 6% 7% 8% 183, 755 186, 142 188,618 591,185 $93, 848 Discussion: 1. What generalizations can you make from the annuity amounts reflected in the analysis table above with regards to the different strategies taken by the families? That is, from a purely financial aspect of the calculations in your table what generalizations could you make regarding the two different strategies? 1 5. Note the dates of the advice columns. How might market performance figure in to their advice they gave at that time? 6. Why do you think Sharon Epperson's advice at the end specifically calls attention to an assumption of whether you are "debt-free and maxing out your 401(k) and IRAs?" 7. If you were to pay extra principal on a mortgage, when is the best time to do it (early or later in the loan process) and why? 8. When you pay extra principal on a loan, describe whether you feel you are actually earning interest on that money or not. That is, how does the old adage "a penny saved is a penny