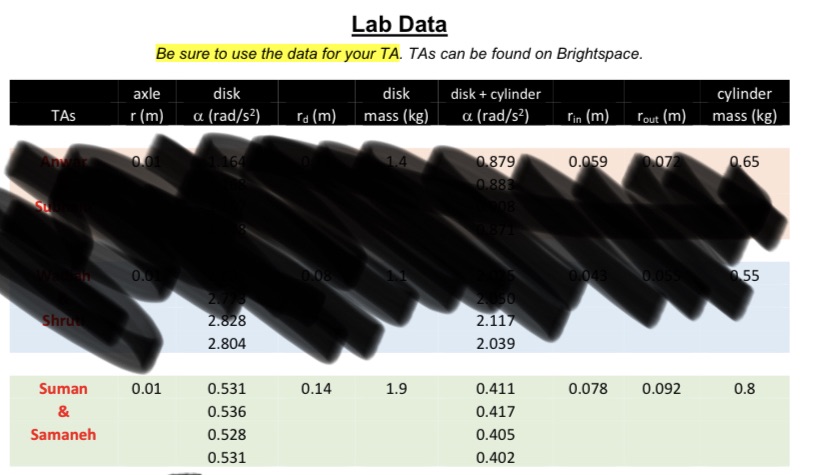
PROCEDURE1. DETERMINING THE MOMENT OF INERTIA OF THE DISK1.1 SETUPAttach the disk by itself to the top of the axle. Hang a 100 g mass to the cord that is wound around the axle and record the mass (in kg) in Excel. Using the digital calipers provided, measure the diameter (r) of the axle the cord is wound around and record the value in Excel (the data for this lab is at the end of this document). Wind up the cord by rotating the disk.1.2 MEASURING ANGULAR ACCELERATIONOpen the "moment of inertia" icon, click on "Collect", and release the mass. As the mass falls Logger Pro will plot the angular acceleration of the disk. Use the statistics tool to determine the average angular acceleration (a) and record it in Excel. Repeat three more times to get four values for a. Using these four, calculate (in Excel) your average angular (davg) acceleration and the standard deviation, 0g.1.3 MoMENT OF INERTIA OF DISKUse Equation 4 (from the theory) to calculate the moment of inertia of the grey disk. Due to the nature of Equation 6 the determination of uncertainty for this experiment is complex but a good estimate of percent uncertainty is (Oa/davg) 100% (note that this assumes no uncertainty in r, m or g). Use this estimate to calculate the percent uncertainty of your moment of inertia.1.4 CALCULATED MASS OF DISKUsing the wooden ruler, measure the radius of the grey disk (ra). Using your moment of inertia (from the previous section), use Equation 1 to calculate the mass of the disk (ma). Use the same percent uncertainty you determined for moment of inertia to calculate the absolute uncertainty of your calculated disk mass.1.5 WEIGH THE DISKUsing the scale at the back of the room, weigh the disk and record the mass in your Excel file. (YouwIll be comparing your calculated disk mass to the actual mass in your report.1.6 ADDING THE HOLLOW CYLINDERPlace the hollow metal cylinder on top of the grey disk in the groove provided. Repeat step 1.2 with the hollow cylinder on top, again finding the average angular acceleration (and standard deviation) of four trials.1.7 MOMENT OF INERTIA OF HOLLOW CYLINDERUse Equation 4 to calculate the moment of inertia of the combined disk and cylinder. As you did in 1.3, estimate percent uncertainty using your a and avg of the disk + cylinder combination. Use Equation 3 (with your calculated moment of inertia of the disk alone) to calculate the moment of inertia of the hollow cylinder. The percent uncertainty for the cylinder alone is the same as for the cylinder and disk together.1.8 EXPECTED MASS OF HOLLOW CYLINDERUsing the wooden ruler, measure the inner (rin) and outer (rout) radii of the cylinder. Use Equation 2 (and the moment of inertia of the cylinder) to calculate the mass of the cylinder (mc). Also calculate theAPHY106 Lab 5Rotational Motionabsolute uncertainty of your calculated cylinder mass, using the percent uncertainty you calculated (in the previous step) for the moment of inertia of the cylinder.1.9 WEIGH THE CYLINDERUsing the scale at the back of the room, weigh the cylinder and record the mass in your Excel file.(You will be comparing your calculated cylinder mass with the actual mass in your report.)Before you upload your lab report, carefully read the grading comments on Brightspace for your previous reports.LAB REPORT QUESTIONS (Answer each in a separate paragraph in your results section.)1. What was your calculated moment of inertia and mass for the disk? What was the percent error between your calculated mass and the measured mass of the disk? Would you say the two agree?Why or why not?2. Repeat question 1 for the hollow cylinder.3. Differences between your calculated masses and the measured values may be due to factors not considered in the theory section of this lab. What do you think these other factors that could cause the discrepancies may have been?THEORYMoment of inertia is analogous to mass for linear motion and is a measure of how much an object resists acceleration from a torque. Unlike mass, the moment of inertia of a particular object is not fixed but depends on how the object is rotating. In this lab a solid flat disk and a hollow cylinder will both be rotated about their central axes, and the relevant moment of inertia () equations arelaisk = = mara(Equation 1)Icylinder = ?mc(rin + rout)(Equation 2)where ra is the disk radius and in and rout are the inner and outer radii of the hollow cylinder and mo and mc are the mass of each respectively. When both objects are rotating together around the same shared axis, the total moment of inertia is the sum of the individual moments of inertia:Idisk+cylinder = Idisk + Icylinder(Equation 3)When forces are used to rotate an object, we say the force creates a torque. In this experiment, the objects will be rotationally accelerated via the torque from a falling mass (m) connected to an axle by a cord. The net force on the mass is given by the difference between the force of gravity (mg) and the tension on the cord:F = mg -T = maT =m(g - a)The tension from the cord provides the torque (r) and can be expressed in terms of the moment of inertia:cord attached to masst= la = Tr+ T=1torque = Tr = lawhere r is the radius of the axle. The angularaxleacceleration (a) is related to the linear acceleration (a) of the mass by0 = i%Combing the two equations for tension (T) and converting all accelerations to angular values gives'(g -ra)(Equation 4)

Lab Data Be sure to use the data for your TA. TAs can be found on Brightspace. axle disk disk disk + cylinder cylinder TAs r (m) a (rad/s2) I'd (m) mass (kg) o (rad/s2) Fin (m) out (m) mass (kg) 64 14 0.879 0.059 1.07 0. 65 0.883 1871 0.0 0.043 0.053 0 55 Shru 2.828 2.117 2.804 2.039 Suman 0.01 0.531 0.14 1.9 0.411 0.078 0.092 0.8 & 0.536 0.417 Samaneh 0.528 0.405 0.531 0.402