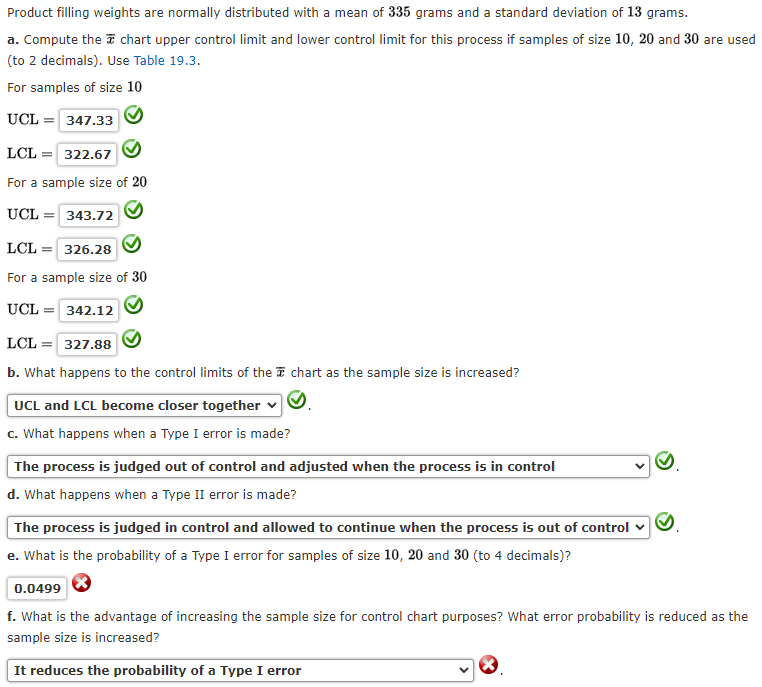Product filling weights are normally distributed with a mean of 335 grams and a standard deviation of 13 grams. a. Compute the x chart upper control limit and lower control limit for this process if samples of size 10 , 20 and 30 are used (to 2 decimals). Use Table 19.3. For samples of size 10 UCL= LCL= For a sample size of 20 UCL= LCL= For a sample size of 30 UCL= LCL= b. What happens to the control limits of the x chart as the sample size is increased? c. What happens when a Type I error is made? The process is judged out of control and adjusted when the process is in control d. What happens when a Type II error is made? The process is judged in control and allowed to continue when the process is out of control e. What is the probability of a Type I error for samples of size 10,20 and 30 (to 4 decimals)? f. What is the advantage of increasing the sample size for control chart purposes? What error probability is reduced as the sample size is increased