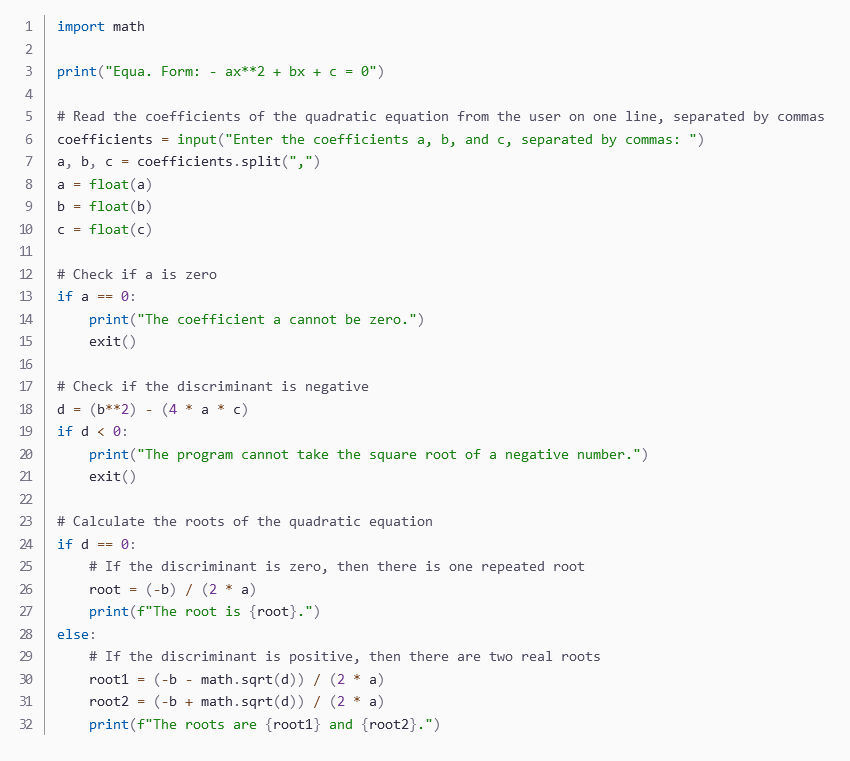
Program 5 Quadratic Equation with File I/O and Formatted Output You are to modify your Program 2 and/or Program 3 to do/include the following: Read the coefficients of the quadratic, 3 coefficients per line (the coefficients will be separated by at least one space, possibly more), from an input file whose name is specified by the user. You should check for existence of the input file and terminate with an error message if the input file cannot be opened. Your program should continue processing sets of coefficients until the end of the input file is reached. Your program should output, to an output file whose name is specified by the user, 1 line per set of coefficients processed. Your output lines should be formatted EXACTLY as those shown on "Attachment A". Your program should make sure that the output file was successfully opened before attempting to process any data. Your program should count how many sets of coefficients it processes and at the end of your program, output that value to the user. Your script file should look similar to the script file shown in "Attachment B", of course including a "cat" of your program at the beginning. Run your program for the two data files as shown in "Attachment B". Include any other test cases which you think are needed. You may find the following UNIX commands helpful in completing this assignment: whoami pwd diff ATTACHMENT A 1.000: Two solutions for x: 2.000: One solution for x: 2.200: Two solutions for x: 5.000, c= -3.000: Two solutions for x: For a= 2.000, b= 5.000, c= and -2.281 For a= 2.000, b= 4.000, c= For a= 5.500, b= 8.000, c= and -1.086 For a= -2.000, b= and 1.500 -0.219 -1.000 -0.368 1.000 For a= 1.000, b= 2.000, c= 3.000: Can not solve, b^2 - 4ac negative. For a= 0.000, b= 5.000, c= 10.000: Not a quadratic equation if a = 0 0.000 For a= 5.000, b= 10.000, c= 0.000: Two solutions for x: and -2.000 For a= 10.000, b= 0.000, c= 5.000: Can not solve, b^2 negative. ERROR: Input must have 3 coefficients, line read had 2 For a= 6.457, b= 7.735, c=100.787: Can not solve, b^2 - 4ac negative. 4ac ATTACHMENT B wbeeche001@grace$ pgm5.pl Input the name of the file which has the coefficients of the quadratic equation (a, b, and c), one set per line: /home/wbeech0001/LCC/cit145/data/pgm5.short.input Input the name of the output file you wish to create: pgm5.short.output This program is being executed by wbeeche001 from /home/wbeeche001/LCC/cis145/working/pgm5 Its input file is /home/wbeeche001/LCC/cit145/data/pgm5.short.input Its output file is pgm5.short.output 10 equations processed wbeeche001@grace$ diff pgm5.short.output /home/wbeeche001/LCC/cis144/data/pgm5.short.output wbeeche001@grace$ pgm5.pl Input the name of the file which has the coefficients of the quadratic equation (a, b, and c), one set per line: /home/wbeech0001/LCC/cit144/data/pgm5.long.input Input the name of the output file you wish to create: pgm5.long.output This program is being executed by wbeech0001 from /home/wbeeche001/LCC/cis145/working/pgm5 Its input file is /home/wbeeche001/LCC/cit144/data/pgm5.long.input Its output file is pgm5.long.output 200 equations processed wbeech0001@grace$ 1 import math 2 3 print("Equa. Form: ax**2 + bx + c = 0") 4 5 # Read the coefficients of the quadratic equation from the user on one line, separated by commas 6 coefficients = input("Enter the coefficients a, b, and c, separated by commas: ") 7 a, b, c = coefficients.split(",") 8 float(a) 9 10 11 12 13 14 15 16 17 9 9 8 12 | 18 19 20 22 23 24 25 26 27 a = b float (b) C = float (c) 29 30 31 32 # Check if a is zero if a == 0: print("The coefficient a cannot be zero.") exit() # Check if the discriminant is negative d = (b**2) (4* a * c) if d < 0: print("The program cannot take the square root of a negative number.") exit() # Calculate the roots of the quadratic equation if d == 0: # If the discriminant is zero, then there is one repeated root root = (-b) / (2* a) print (f"The root is {root}.") 28 else: # If the discriminant is positive, then there are two real roots root1 = (-b math.sqrt(d)) / (2 * a) root2 (-b + math.sqrt(d)) / (2 * a) print (f"The roots are {root1} and {root2}.") =