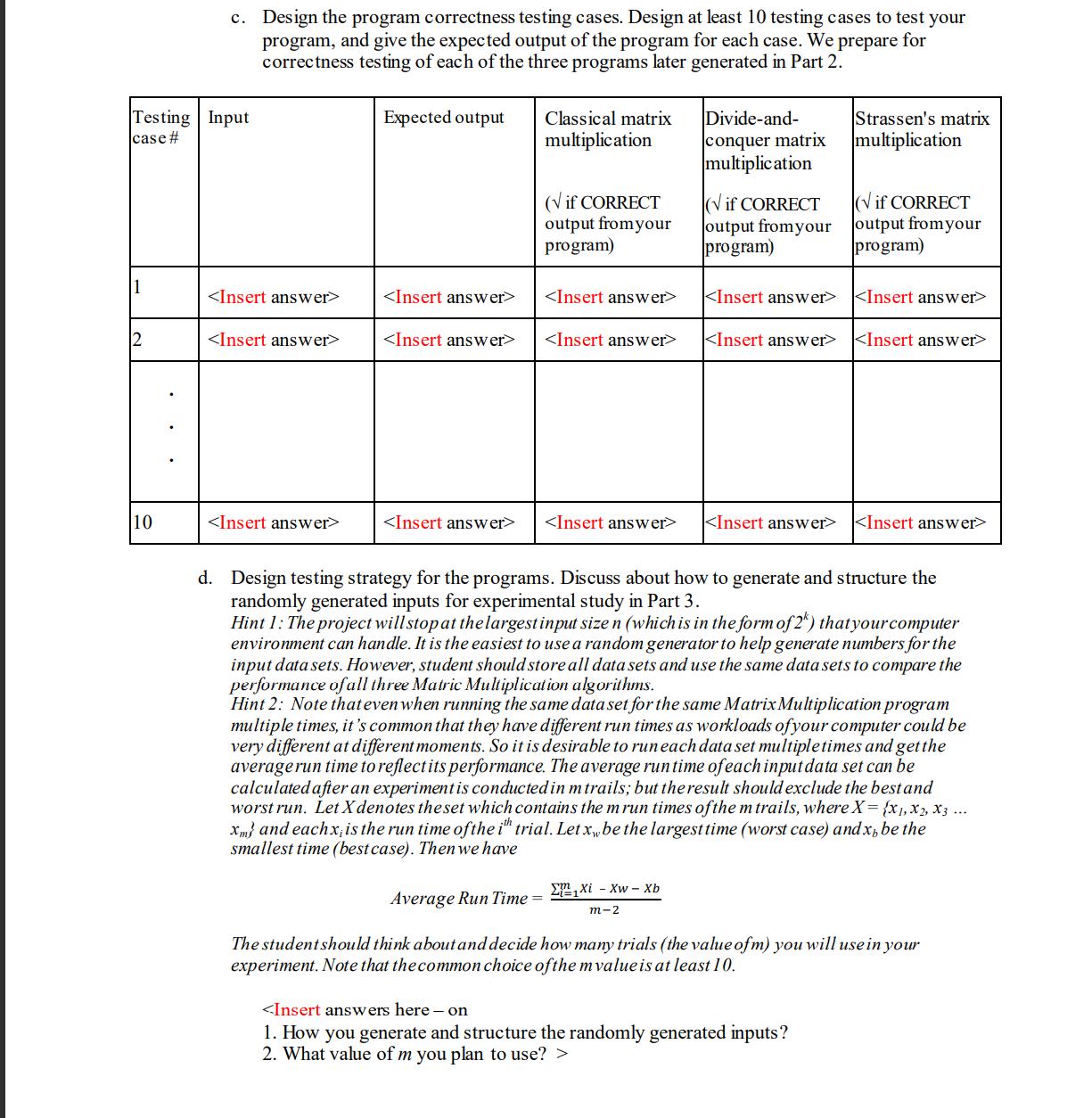
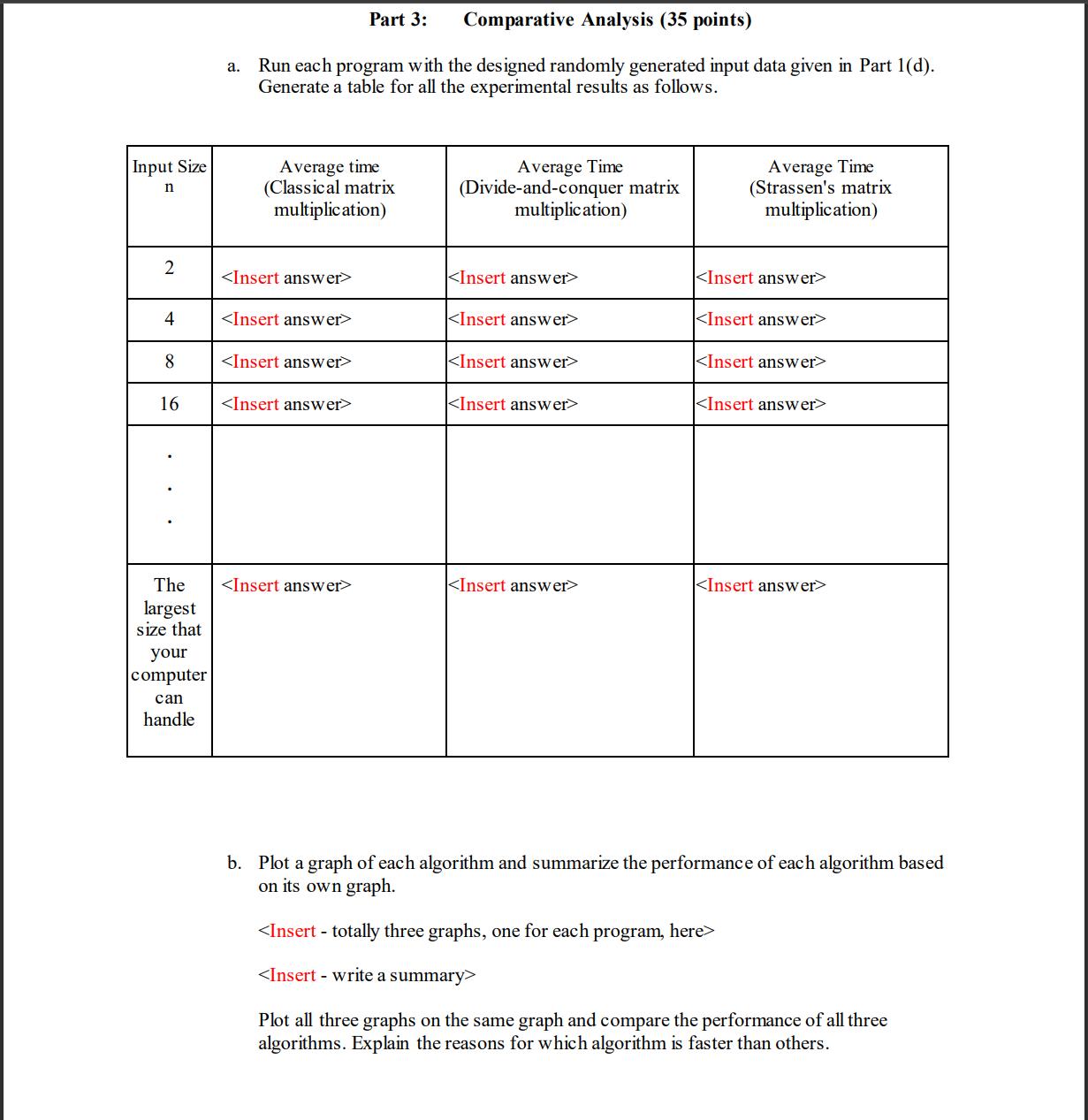
Program the following algorithms that we covered in the class: a. Classical matrix multiplication b. Divide-and-conquer matrix multiplication Strassen's matrix multiplication C. You can use either Java, or C++ for the implementation. The objective of this project is to help student understand how above three algorithms operates and their difference in run-time complexity (average- case scenario). The project will be divided into three phases to help you to accomplish above tasks. They are Part 1: Design and Theoretical analysis, Part 2: Implementation, and Part 3: Comparative Analysis. This project will ask student to conduct the matrix multiplication on the numeric data type. You can implement the above three algorithms in your choice of data structures based on the program language of your choice. Note that you always try your best to give the most efficient program for each problem. Let the matrix size be n x n. Carry out a complete test of your algorithms with n = 2, 4, 8, 16, 32, 64, 128, 256,... (up to the largest size of n that your computer can handle). The size of the input will be limited in the power of 2. They are 2, 4, 8, 16, 32 up to 2k where 2k is the largest size of the input that your computer can handle or your program might quit at size of 2k due to running out of memory. The reason for the power of 2 is to ease the programming component of the assignment. Submission Instructions: After the completion of all three parts, Part 1, Part 2 and Part 3, submit (upload) the following files to Canvas: three program files of three algorithms or one program file including all three algorithms (your choice of programming language with proper documentation) this document in pdf format (complete it with all the answers) 1 Part 1: Design & Theoretical Analysis (30 points) a. Complete the following table for theoretical worst-case complexity of each algorithm. Design & Theoretical Analysis (30 points) a. Complete the following table for theoretical worst-case complexity of each algorithm. Also need to describe how the worst-case input of each algorithm should be. Algorithm Classical matrix multiplication Divide-and-conquer matrix multiplication Part 1: Strassen's matrix multiplication theoretical worst-case complexity describe the worst-case input b. Design the program by providing pseudocode or flowchart for each sorting algorithm. c. Design the program correctness testing cases. Design at least 10 testing cases to test your program, and give the expected output of the program for each case. We prepare for correctness testing of each of the three programs later generated in Part 2. Testing Input case # 10 Expected output Classical matrix multiplication ( if CORRECT output from your program) Divide-and- conquer matrix multiplication Xi-Xw- Xb m-2 (if CORRECT output from your program) KInsert answer> Strassen's matrix multiplication (if CORRECT output from your program) KInsert answer> KInsert answer> d. Design testing strategy for the programs. Discuss about how to generate and structure the randomly generated inputs for experimental study in Part 3. Hint 1: The project will stop at the largest input size n (which is in the form of 2) that your computer environment can handle. It is the easiest to use a random generator to help generate numbers for the input data sets. However, student should store all data sets and use the same data sets to compare the performance of all three Matric Multiplication algorithms. Hint 2: Note that even when running the same data set for the same Matrix Multiplication program multiple times, it's common that they have different run times as workloads of your computer could be very different at different moments. So it is desirable to run each data set multiple times and get the average run time to reflect its performance. The average run time of each input data set can be calculated after an experiment is conducted in m trails; but the result should exclude the best and worst run. Let X denotes the set which contains the m run times of the m trails, where X = {x1, x2, X3 ... Xm} and eachx, is the run time of the ith trial. Let x, be the largest time (worst case) andx, be the smallest time (best case). Then we have Average Run Time = The student should think about and decide how many trials (the value of m) you will use in your experiment. Note that the common choice of the m value is at least 10. KInsert answer> Input Size n 2 4 8 16 The largest size that your computer can handle Comparative Analysis (35 points) a. Run each program with the designed randomly generated input data given in Part 1(d). Generate a table for all the experimental results as follows. Average time (Classical matrix multiplication) Part 3: Average Time (Divide-and-conquer matrix multiplication) Average Time (Strassen's matrix multiplication) b. Plot a graph of each algorithm and summarize the performance of each algorithm based on its own graph. Plot all three graphs on the same graph and compare the performance of all three algorithms. Explain the reasons for which algorithm is faster than others. c. Compare the theoretical results in Part 1(a) and empirical results here. Explain the possible factors that cause the difference. d. Give a spec of your computing environment, e.g. computer model, OS, hardware/software info, processor model and speed, memory size, ... e. Conclude your report with the strength and constraints of your work. At least 200 words. Note: It is reflection of this project. Ask yourself if you have a chance to re-do this project again, what you will do differently (e.g. your computing environment, programing language, data structure, data set generation, ...) in order to design a better performance evaluation experiment. Program the following algorithms that we covered in the class: a. Classical matrix multiplication b. Divide-and-conquer matrix multiplication Strassen's matrix multiplication C. You can use either Java, or C++ for the implementation. The objective of this project is to help student understand how above three algorithms operates and their difference in run-time complexity (average- case scenario). The project will be divided into three phases to help you to accomplish above tasks. They are Part 1: Design and Theoretical analysis, Part 2: Implementation, and Part 3: Comparative Analysis. This project will ask student to conduct the matrix multiplication on the numeric data type. You can implement the above three algorithms in your choice of data structures based on the program language of your choice. Note that you always try your best to give the most efficient program for each problem. Let the matrix size be n x n. Carry out a complete test of your algorithms with n = 2, 4, 8, 16, 32, 64, 128, 256,... (up to the largest size of n that your computer can handle). The size of the input will be limited in the power of 2. They are 2, 4, 8, 16, 32 up to 2k where 2k is the largest size of the input that your computer can handle or your program might quit at size of 2k due to running out of memory. The reason for the power of 2 is to ease the programming component of the assignment. Submission Instructions: After the completion of all three parts, Part 1, Part 2 and Part 3, submit (upload) the following files to Canvas: three program files of three algorithms or one program file including all three algorithms (your choice of programming language with proper documentation) this document in pdf format (complete it with all the answers) 1 Part 1: Design & Theoretical Analysis (30 points) a. Complete the following table for theoretical worst-case complexity of each algorithm. Design & Theoretical Analysis (30 points) a. Complete the following table for theoretical worst-case complexity of each algorithm. Also need to describe how the worst-case input of each algorithm should be. Algorithm Classical matrix multiplication Divide-and-conquer matrix multiplication Part 1: Strassen's matrix multiplication theoretical worst-case complexity describe the worst-case input b. Design the program by providing pseudocode or flowchart for each sorting algorithm. c. Design the program correctness testing cases. Design at least 10 testing cases to test your program, and give the expected output of the program for each case. We prepare for correctness testing of each of the three programs later generated in Part 2. Testing Input case # 10 Expected output Classical matrix multiplication ( if CORRECT output from your program) Divide-and- conquer matrix multiplication Xi-Xw- Xb m-2 (if CORRECT output from your program) KInsert answer> Strassen's matrix multiplication (if CORRECT output from your program) KInsert answer> KInsert answer> d. Design testing strategy for the programs. Discuss about how to generate and structure the randomly generated inputs for experimental study in Part 3. Hint 1: The project will stop at the largest input size n (which is in the form of 2) that your computer environment can handle. It is the easiest to use a random generator to help generate numbers for the input data sets. However, student should store all data sets and use the same data sets to compare the performance of all three Matric Multiplication algorithms. Hint 2: Note that even when running the same data set for the same Matrix Multiplication program multiple times, it's common that they have different run times as workloads of your computer could be very different at different moments. So it is desirable to run each data set multiple times and get the average run time to reflect its performance. The average run time of each input data set can be calculated after an experiment is conducted in m trails; but the result should exclude the best and worst run. Let X denotes the set which contains the m run times of the m trails, where X = {x1, x2, X3 ... Xm} and eachx, is the run time of the ith trial. Let x, be the largest time (worst case) andx, be the smallest time (best case). Then we have Average Run Time = The student should think about and decide how many trials (the value of m) you will use in your experiment. Note that the common choice of the m value is at least 10. KInsert answer> Input Size n 2 4 8 16 The largest size that your computer can handle Comparative Analysis (35 points) a. Run each program with the designed randomly generated input data given in Part 1(d). Generate a table for all the experimental results as follows. Average time (Classical matrix multiplication) Part 3: Average Time (Divide-and-conquer matrix multiplication) Average Time (Strassen's matrix multiplication) b. Plot a graph of each algorithm and summarize the performance of each algorithm based on its own graph. Plot all three graphs on the same graph and compare the performance of all three algorithms. Explain the reasons for which algorithm is faster than others. c. Compare the theoretical results in Part 1(a) and empirical results here. Explain the possible factors that cause the difference. d. Give a spec of your computing environment, e.g. computer model, OS, hardware/software info, processor model and speed, memory size, ... e. Conclude your report with the strength and constraints of your work. At least 200 words. Note: It is reflection of this project. Ask yourself if you have a chance to re-do this project again, what you will do differently (e.g. your computing environment, programing language, data structure, data set generation, ...) in order to design a better performance evaluation experiment.